Higher Derivatives and Concavity
TLDRThis lesson delves into the concept of higher derivatives, also known as higher order derivatives, which are essentially the derivatives of derivatives. The instructor explains the notation for these derivatives and illustrates how they are used to find the slope of a function's derivative. The video covers finding the first four derivatives of a given function and introduces the product rule for differentiation when dealing with functions expressed as a product of multiple terms. The applications of higher derivatives in physics for understanding motion, such as position, velocity, and acceleration, are also discussed. Furthermore, the lesson explores the use of second derivatives to analyze the concavity of a function and identify inflection points, which are critical in various fields, including economics where they signify points of diminishing returns. The script is educational, providing a clear understanding of higher derivatives and their practical applications.
Takeaways
- 📚 Higher derivatives are the derivatives of derivatives, used to find the slope of the original function's derivative.
- 🔢 Notation for higher derivatives: F' for the first derivative, F'' for the second, F''' for the third, and Fn for the nth derivative.
- 📈 The concept of concavity describes the direction in which a graph opens, either concave up (like a U facing up) or concave down (like a U facing down).
- 🔍 To find higher derivatives, you can apply differentiation rules such as the power rule and the product rule, especially for functions in factored form.
- 🚀 Applications of higher derivatives include describing motion in physics, where position, velocity, and acceleration are all represented by derivatives.
- ✅ The second derivative test can be used to determine intervals of concavity and potential inflection points by finding where the second derivative is zero or undefined.
- 🤔 A point of inflection indicates a change in concavity, but a change in concavity does not always indicate an inflection point; it could be a discontinuity.
- 📈 In economics, an inflection point on a revenue function is known as a point of diminishing returns, where the rate of increase in revenue begins to slow down.
- 📌 To confirm inflection points, it's necessary to check the graph or plug in the critical numbers into the original function to see where the concavity changes.
- ⚖️ Velocity is the rate of change of position with respect to time, and acceleration is the rate of change of velocity with respect to time, both of which are found using derivatives.
- 🔑 The product rule for differentiation extends to multiple products, where the derivative of a product of 'n' functions involves the sum of 'n' products of the form f'gh + fg'h + ... + fgh'.
Q & A
What is the definition of a higher derivative?
-A higher derivative refers to the process of finding the derivative of a derivative, also known as higher order derivatives. It involves calculating the slope of the original function's derivative.
How do you denote the second derivative of a function?
-The second derivative is denoted as 'F double Prime of X' or simply by using the number '2' in parentheses, as in 'F(2)(X)', to avoid confusion with exponents.
What is the role of higher order derivatives in the context of motion?
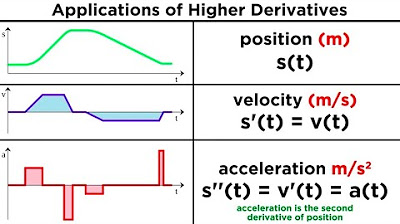
-Higher order derivatives are used to describe different aspects of motion. The first derivative represents velocity (rate of change of position with respect to time), and the second derivative represents acceleration (rate of change of velocity with respect to time).
How can you find the first four derivatives of a given function?
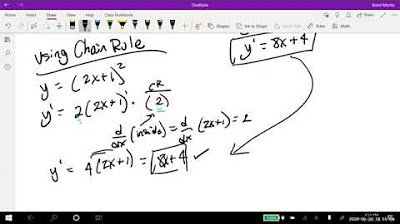
-You can find the first four derivatives by applying the power rule iteratively. After finding the first derivative, you take the derivative of that result to find the second derivative, and so on until you find the fourth derivative.
What is the product rule for differentiation, and how does it apply when you have more than two functions being multiplied?
-The product rule states that the derivative of a product of two functions is the derivative of the first times the second plus the first times the derivative of the second. For more than two functions, you extend this rule by including a sum of products, each consisting of one function's derivative and another function.
How does the degree of the exponent change with each differentiation?
-With each differentiation, the degree of the exponent decreases by one. This is because differentiation is essentially applying the power rule, which reduces the power by one for each derivative.
What is the concept of concavity in mathematics, and how does it relate to higher order derivatives?
-Concavity refers to the direction in which a graph opens, either upward (concave up) or downward (concave down). It is related to higher order derivatives because if a function is concave up, its first derivative is increasing, which means the second derivative is positive, and vice versa for concave down.
How can you identify an inflection point on a graph?
-An inflection point is a point where the concavity of a graph changes. It can be identified by finding where the second derivative changes sign (from positive to negative or vice versa), indicating a change from concave up to concave down or vice versa.
What is the economic significance of an inflection point in a revenue function?
-In economics, an inflection point in a revenue function is known as a point of diminishing returns. It signifies that the rate of increase in revenue is slowing down, meaning that the additional revenue generated by producing more items is decreasing.
How do you use the second derivative test to determine intervals of concavity and potential inflection points?
-You find the second derivative of the function and then determine its critical numbers (where the second derivative is zero or undefined). By testing values before, between, and after these critical numbers, you can determine whether the function is concave up or concave down in different intervals. Points where the concavity changes are potential inflection points.
Why is it important to differentiate between a change in concavity and an inflection point?
-A change in concavity always indicates an inflection point, but an inflection point is not guaranteed by a mere change in concavity. It's crucial to verify with a graph or further analysis because the change could be due to other factors, such as a discontinuity in the function.
Outlines
📚 Introduction to Higher Derivatives and Applications
This paragraph introduces the concept of higher derivatives, which are essentially derivatives of derivatives. It explains the notation used for first, second, third, and higher order derivatives. The paragraph also touches on the application of higher derivatives in various fields and starts with an example of finding the first four derivatives of a given function using the power rule. It further discusses the product rule for differentiation when dealing with functions expressed as a product of multiple factors.
🔢 Derivatives in Motion and Physics
The second paragraph explores the application of higher order derivatives in describing motion, which is a common topic in physics. It defines three key terms related to motion: position, velocity, and acceleration. Position is the distance from a starting point, velocity is the rate of change of position over time, and acceleration is the rate of change of velocity over time. The paragraph provides a detailed example of how to calculate these for an object thrown upward from a cliff with a specific initial velocity and initial height.
📉 Understanding Concavity and Inflection Points
This paragraph delves into the concept of concavity and inflection points in functions. It explains how the sign of the second derivative can indicate whether a function is concave up (positive second derivative) or concave down (negative second derivative). The paragraph also discusses how a point of inflection, where concavity changes, can be identified through the second derivative. It emphasizes that while a point of inflection always indicates a change in concavity, a change in concavity does not always result in an inflection point.
🔍 Second Derivative Test for Concavity
The fourth paragraph focuses on the second derivative test to determine the intervals of concavity and potential inflection points of a function. It outlines the process of finding critical numbers of the second derivative and testing values before, between, and after these critical numbers to assess concavity. The paragraph includes an example using a polynomial function, which shows how to apply the test and interpret the results to find intervals of concavity and inflection points.
📈 Point of Diminishing Returns in Economics
The fifth paragraph discusses the economic application of inflection points, specifically in the context of a point of diminishing returns. It explains that an inflection point on a revenue function indicates a slowdown in the rate of increase of revenue. The paragraph illustrates how the second derivative, which represents the rate of change of the rate of change, can signal a point where the revenue begins to increase at a decreasing rate. This concept is important for understanding optimal production levels in economic models.
🗣️ Conclusion and Offering Help
The final paragraph concludes the lesson and offers help to students who may have further questions or need additional assistance. It summarizes the key points covered in the lesson and encourages students to reach out for support, emphasizing the importance of understanding higher derivatives, their applications, and the concepts of concavity and inflection points.
Mindmap
Keywords
💡Higher Derivatives
💡Concavity
💡Inflection Points
💡Product Rule
💡Position Function
💡Velocity
💡Acceleration
💡Second Derivative Test
💡Critical Numbers
💡Point of Diminishing Returns
💡Rational Function
Highlights
Introduction to higher derivatives, which are essentially the derivatives of derivatives.
Notation for higher derivatives includes F Prime for the first derivative, F double Prime for the second, and numbers in parentheses for the fourth and higher order derivatives.
Derivatives represent the slope of a function, with higher order derivatives representing the slope of the derivative functions.
Finding higher order derivatives involves applying the power rule to polynomial functions.
Differentiation rules, such as the product rule, can be extended to handle products of multiple functions.
Applications of higher order derivatives include motion, physics, and economics, with examples like position, velocity, and acceleration in motion.
The concept of concavity and inflection points is introduced, with concavity referring to the direction of the 'openness' of a graph.
A function is concave up when its first derivative is increasing and concave down when its first derivative is decreasing.
Second derivative test can be used to find intervals of concavity and potential inflection points by analyzing critical numbers.
An inflection point always indicates a change in concavity, but a change in concavity does not always result in an inflection point.
Practical application of inflection points in economics is illustrated through the concept of a point of diminishing returns.
The revenue function example demonstrates how the rate of increase in revenue slows down after an inflection point, indicating diminishing returns.
The importance of verifying inflection points through graph analysis is emphasized, as not all changes in concavity result in inflection points.
The process of finding higher order derivatives involves simplifying expressions and applying differentiation rules effectively.
Graphical representation of functions helps in visualizing and confirming the mathematical findings related to concavity and inflection points.
The transcript provides a comprehensive understanding of higher derivatives, their applications, and the significance of concavity and inflection points in various fields.
The instructional approach includes step-by-step differentiation, application of rules, and interpretation of results in context.
The use of examples and real-world applications helps in grasping the abstract concepts of higher derivatives and their significance.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: