Math 1325 Lecture 9 8 - Higher Order Drivatives
TLDRThis lecture on Math 1325, Section 9.8, delves into the concept of higher-order derivatives, which represent the rate of change of the rate of change. Using the example of cell phone subscriber growth, the lecturer illustrates how derivatives can measure growth rates at different points in time. The video covers the notation and calculation of first, second, and higher-order derivatives, emphasizing the process of differentiation. Practical problems, including modeling cell phone subscriber numbers and a physics problem on particle acceleration, are solved to demonstrate the application of derivatives in real-world scenarios. The lecture concludes with an analysis of how the rate of subscriber growth is slowing down, despite an increase in the absolute number of subscribers, highlighting the utility of second derivatives in understanding changes in rates of change.
Takeaways
- 📚 Higher-order derivatives represent the rate of change of the rate of change, which can be understood through examples such as the growth of cellphone subscribers over time.
- 📈 To find the rate of change at specific points, one can compare the steepness of the tangent lines at those points on a graph.
- 🔢 The notation for the first derivative is F'(x) or dy/dx, while the second derivative is F''(x) or d^2y/dx^2, and so on for higher derivatives.
- 🧮 Taking the second derivative of a function involves differentiating the first derivative, which can be done using standard differentiation rules.
- 📉 A negative second derivative indicates that the rate of change (i.e., the slope of the tangent line) is decreasing, even if the overall quantity is still increasing.
- 🌟 The process of finding higher-order derivatives involves applying differentiation rules such as the power rule and the chain rule.
- 📌 The derivative of a function gives the instantaneous rate of change at a point, which is the slope of the tangent line at that point on the graph.
- 📊 The second derivative can be used to analyze how the rate of change itself is changing over time, providing insight into acceleration or deceleration.
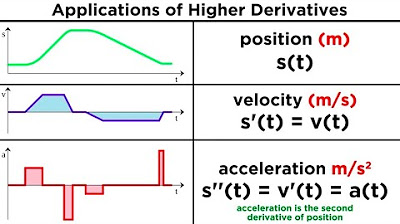
- 🔬 In physics, acceleration is the rate of change of velocity, which is the second derivative of position with respect to time.
- ✅ Practice is key to becoming proficient in finding derivatives, as demonstrated by the step-by-step solutions provided in the script.
- 🌐 Real-world data, such as the number of cellphone subscribers worldwide, can be modeled mathematically and analyzed using derivatives to understand trends and changes over time.
Q & A
What is the concept of higher-order derivatives?
-Higher-order derivatives refer to the concept of taking the derivative of a derivative. It represents the rate of change of the rate of change, which can be used to analyze how the rate of change itself is changing over time or in relation to another variable.
How is the second derivative of a function notated?
-The second derivative of a function is denoted by either 'y'' (y double prime) or 'd²y/dx²'. It represents the derivative of the first derivative of the function.
What does a steeper slope on a graph indicate?
-A steeper slope on a graph indicates a faster rate of change. In the context of the script, it means that the number of cell phone subscribers was growing more rapidly at that point on the graph.
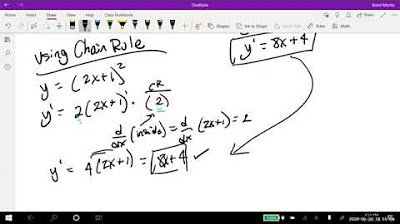
What is the first step in finding the second derivative of the function y = √(2x - 1)?
-The first step is to find the first derivative of the function using the chain rule. This involves bringing the power down in front and applying the rule to the outer function (2x - 1) raised to the power of 1/2.
How is the third derivative of a function represented?
-The third derivative of a function is represented as 'f''' (f triple prime) or 'd³y/dx³'. It is the derivative of the second derivative.
What does the negative exponent in the derivative of y = √(2x - 1) signify?
-A negative exponent signifies that the term should be taken as the reciprocal of the base raised to the absolute value of the exponent. In the context of the radical form, it means that the expression should be under the radical and the exponent should be 3, as in 1/√(2x - 1)^3.
What does the instantaneous rate of change of a function represent?
-The instantaneous rate of change of a function represents the derivative at a specific point. It gives the slope of the tangent line to the curve of the function at that point, which can be interpreted as the velocity or speed at that instant.
What is the physical interpretation of the second derivative in the context of the cellphone subscribers example?
-In the context of the cellphone subscribers example, the second derivative represents how fast the growth rate of subscribers is changing. A negative second derivative indicates that the rate of growth is slowing down, even though the overall number of subscribers is still increasing.
How can you find the acceleration of a particle given its distance-time equation?
-To find the acceleration of a particle, you first find the velocity by taking the first derivative of the distance-time equation with respect to time. Then, you find the acceleration by taking the derivative of the velocity, which is the second derivative of the distance-time equation.
What does the term 'acceleration' represent in physics?
-In physics, 'acceleration' represents the rate of change of velocity over time. It is the second derivative of the position with respect to time and indicates how quickly the velocity of an object is changing.
What is the significance of finding higher-order derivatives in real-world applications?
-Higher-order derivatives are significant in real-world applications as they can provide insights into not just the rate of change but also the behavior of how that rate of change is changing over time. This can be useful in various fields such as economics, physics, engineering, and more, where understanding the dynamics of growth, decay, or motion is crucial.
Outlines
📈 Understanding Higher-Order Derivatives
This paragraph introduces the concept of higher-order derivatives, specifically second and third derivatives, which represent the rate of change of the rate of change. The lecturer uses the example of cell phone subscribers' growth to illustrate how derivatives can show how fast a quantity is changing at specific points. The process of taking derivatives is explained step by step, with an example of finding the second derivative of a function. Notations for first, second, and higher-order derivatives are discussed, and the concept is applied to find the rate of change of cell phone subscribers over time.
📊 Derivatives in Real-World Data: Cell Phone Subscribers
The second paragraph delves into applying derivatives to real-world data, specifically the growth of cell phone subscribers worldwide. The lecturer guides through finding the first, second, third, and fourth derivatives of a given function, showing how they simplify with each iteration. A model function representing the number of worldwide cell phone subscribers is introduced, and the instantaneous rate of change is calculated for specific years. The second derivative is used to analyze how fast the growth rate is changing, revealing a slowing trend in subscriber growth by 2015 despite an increase in absolute numbers.
🚀 Applying Derivatives to Physics: Acceleration Problem
The final paragraph explores the application of derivatives in physics, focusing on the concept of acceleration. The lecturer presents a formula for the distance traveled by a particle over time and explains that the derivative of this distance with respect to time gives the velocity, while the second derivative gives the acceleration. The process of finding the velocity and acceleration is demonstrated, leading to the conclusion that the acceleration in the given scenario is negative, indicating a decrease in speed over time.
Mindmap
Keywords
💡Higher-order derivatives
💡Rate of change
💡Derivative notation
💡Chain rule
💡Tangent line
💡Second derivative
💡Instantaneous rate of change
💡Acceleration
💡Velocity
💡Power rule
💡Exponential growth
Highlights
Introduction to higher-order derivatives, focusing on the concept of the rate of change of the rate of change.
Use of cellphone subscriber data to illustrate the concept of derivatives in a real-world context.
Derivation of the second derivative of a function, denoted as Y double prime or f prime prime.
Explanation of derivative notations, including first, second, third, and higher-order derivatives.
Practice problem: Finding the second derivative of y = sqrt(2x - 1) using the chain rule.
Transformation of the derivative into radical form to match the original function's format.
Derivation of the first, second, third, and fourth derivatives of a polynomial function.
Demonstration of how derivatives simplify as they progress from the first to the fourth.
Application of derivatives to model the growth of worldwide cellphone subscribers using a mathematical function.
Calculation of the instantaneous rate of change of cellphone subscribers, represented as C prime.
Use of the second derivative to determine the acceleration or deceleration of subscriber growth in 2015.
Interpretation of the negative second derivative indicating a slowing growth rate of cellphone subscribers.
Differentiation between velocity (first derivative) and acceleration (second derivative) in the context of physics.
Calculation of acceleration using the second derivative of distance with respect to time.
Explanation of the significance of a negative acceleration value indicating a decrease in speed.
Integration of International Telecommunications Union data to model and analyze cellphone subscriber growth.
Illustration of the practical application of derivatives in understanding changes in data trends over time.
Emphasis on the importance of understanding higher-order derivatives for analyzing complex rates of change.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: