Higher Order Derivatives (Part 2)
TLDRThe video script delves into the concept of derivatives in calculus, focusing on their practical applications in word problems. It emphasizes that the second derivative, denoted as y double prime, measures the instantaneous rate of change of the first derivative, y prime. The script illustrates this with examples from physics, where the derivative of position (s) gives velocity (v), and the second derivative gives acceleration (a). The concept is further applied to a business context, where the second derivative of the revenue function represents the rate of change in marginal revenue. The script provides step-by-step solutions to find the rate of change at specific points, highlighting the importance of understanding the relationship between derivatives and their rates of change. It concludes by encouraging viewers to review the material and grasp the fundamental idea that each derivative describes the rate of change of its predecessor.
Takeaways
- 📌 The second derivative, denoted as y double prime (y''), measures the instantaneous rate of change of the first derivative, y prime (y').
- 📈 Taking the derivative of a function (y) gives you the rate of change, which is the first derivative (y').
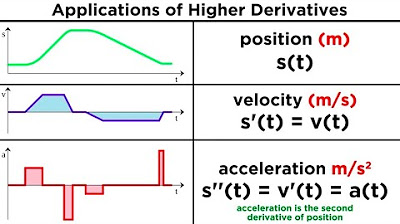
- 🚀 In physics, the derivative of position (s) is velocity (v), and the second derivative of position is acceleration (a).
- ✅ To find the rate of change of y at a specific point, plug the x-value of that point into the first derivative of y.
- 🔍 The second derivative can be found by taking the derivative of the first derivative, which gives you the rate of change of y'.
- 📐 For the given example y = 24x^2 - 4x^3 + x, the second derivative y'' is 48 - 24x.
- 🔢 To find the rate of change of y' at a specific point, substitute the x-value of that point into the second derivative.
- 📚 In the context of business, the revenue function can be given, and its first derivative represents marginal revenue.
- 📉 The rate of change of marginal revenue, which is the derivative of the marginal revenue function, can be found by taking the second derivative of the revenue function.
- 💡 Understanding the relationship between derivatives and their rates of change is crucial for solving word problems involving calculus.
- 🔑 Each higher-order derivative describes the rate of change of the preceding derivative, making it a powerful tool for analyzing various real-world scenarios.
- ✍️ Practice is essential for grasping the concepts of derivatives and their applications, as emphasized by the speaker.
Q & A
What does the second derivative, y double prime, measure?
-The second derivative, y double prime, measures the instantaneous rate of change of y prime, which is the first derivative of y.
How is the second derivative related to the first derivative in terms of their roles?
-The second derivative relates to the first derivative in the same way the first derivative relates to the original function y. It measures the rate of change of the first derivative.
What is the derivative of the position function in the context of physics?
-In physics, the derivative of the position function (denoted as s or y) is velocity (denoted as v or s prime).
What does the derivative of velocity represent?
-The derivative of velocity, which is the second derivative of position, represents acceleration (denoted as a or s double prime).
How can you find the acceleration of a particle at a specific time, given its position function?
-To find the acceleration at a specific time, you first find the velocity function by taking the first derivative of the position function. Then, you find the acceleration function by taking the second derivative of the position function. Finally, you evaluate the acceleration function at the given time.
What is the revenue function given in the script?
-The revenue function given is R(x) = 70x + 0.8x^2 - 0.003x^3, where x is the number of units sold.
How is marginal revenue related to the revenue function?
-Marginal revenue is the first derivative of the revenue function. It represents the rate of change of revenue with respect to the number of units sold.
What does the rate of change of marginal revenue represent?
-The rate of change of marginal revenue, which is the second derivative of the revenue function, represents how quickly the marginal revenue itself is changing.
How do you calculate the rate of change of marginal revenue at a certain number of units?
-To calculate the rate of change of marginal revenue at a certain number of units, you first find the marginal revenue function by taking the derivative of the revenue function. Then, you find the second derivative of the revenue function to get the rate of change of marginal revenue. Finally, you evaluate this second derivative at the specific number of units.
What is the significance of understanding the concept of derivatives in word problems?
-Understanding the concept of derivatives is crucial in word problems as it allows you to calculate rates of change, which are often asked for in problems involving physics, economics, and other fields. It helps in determining how quantities are changing over time or in relation to other variables.
Why is it important to review problems involving derivatives?
-Reviewing problems involving derivatives is important because it helps solidify the understanding of how derivatives represent rates of change and how they can be applied to solve real-world problems. It also aids in recognizing the pattern that each derivative describes the rate of change of the previous one.
What is the final numerical answer for the acceleration of the particle at t equals 6 seconds?
-The acceleration of the particle at t equals 6 seconds is 2.88 meters per second squared.
Outlines
📚 Understanding Second Derivatives in Calculus
This paragraph discusses the concept of second derivatives in calculus, emphasizing their role in measuring the instantaneous rate of change of the first derivative (y prime). The explanation begins with a critical observation that y double prime (the second derivative) is related to y prime in the same way y prime is related to the original function y. This relationship is illustrated through a step-by-step breakdown of a given equation, y = 24x^2 - 4x^3 + x, where the first and second derivatives are calculated. The example further extends to a physics analogy, where the first derivative of position (y) is velocity (v), and the second derivative is acceleration (a). This concept is then applied to find the acceleration of a particle at a specific time, demonstrating the practical application of second derivatives in physics and problem-solving.
🚀 Applying Derivatives to Physics and Business
The second paragraph delves into the application of derivatives in physics and business scenarios. It begins with a physics example where the position (s) of an object is given as a function of time (t), and the task is to find the acceleration at a specific time. The process involves finding the first derivative (velocity function) and the second derivative (acceleration). The example shows that the acceleration can be calculated by taking the second derivative of the position function. The paragraph then transitions to a business context, discussing marginal revenue problems. It explains how the first derivative of the revenue function gives the marginal revenue and the second derivative provides the rate of change of the marginal revenue. An example is worked out to illustrate this concept, highlighting the practical use of derivatives in business analysis.
🤔 Reflecting on the Concept of Higher Order Derivatives
The final paragraph serves as a reflective summary of the concepts discussed in the previous sections. It reinforces the idea that each subsequent derivative describes the rate of change of the previous one. The paragraph emphasizes the importance of understanding why each derivative is being calculated and what is being asked in the problem. It encourages the audience to review the problems and pause to ensure they grasp the concepts. The summary serves as a reminder that while the concepts may be complex, they are fundamental to solving a variety of word problems in both physics and business contexts.
Mindmap
Keywords
💡Instantaneous rate of change
💡Derivative
💡Second derivative
💡Velocity
💡Acceleration
💡Function
💡Marginal revenue
💡Rate of change
💡Physics
💡Word problems
Highlights
The second derivative, denoted as y double prime, measures the instantaneous rate of change of the first derivative, y prime.
The concept of y prime being the rate of change of y is extended to y double prime being the rate of change of y prime.
Derivatives beyond the first order can be used to measure the rate of change of the preceding derivative, with y triple prime measuring the rate of change of y double prime.
The equation y = 24x^2 - 4x^3 + x is translated to find the rate of change of y prime at a given point.
The rate of change of y at a specific point is found by plugging the x value into the derivative of y.
The second derivative, y double prime, is calculated as 48 - 24x, illustrating the rate of change of y prime.
In physics, the derivative of position (s) is velocity (v), and the second derivative is acceleration (a).
The rate of change of velocity is acceleration, which is the third derivative of position.
An example problem involves finding the acceleration of a particle given its position function s(t) = 80 + 7t + 0.08t^3.
The velocity function is found by taking the first derivative of the position function.
Acceleration is found by taking the second derivative of the position function, resulting in 0.48t.
The acceleration of the particle at t = 6 seconds is calculated to be 2.88 meters per second squared.
Velocity is measured in meters per second, and acceleration in meters per second squared.
Marginal revenue problems involve finding the rate of change of revenue with respect to the number of units sold.
The revenue function is given as R(x) = 70x + 0.8x^2 - 0.003x^3, where x is the number of units sold.
Marginal revenue (R prime) is found by taking the first derivative of the revenue function.
The rate of change of marginal revenue (R double prime) is found by taking the second derivative of the revenue function.
The rate of change of marginal revenue at 50 units is calculated by plugging the value into the second derivative function, resulting in 0.7.
The second derivative consistently describes the rate of change of the first derivative, regardless of the order.
Understanding the relationship between derivatives and their rates of change is crucial for solving word problems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: