Unit Circle Trigonometry - Sin Cos Tan - Radians & Degrees
TLDRThis video script offers an in-depth exploration of the unit circle and trigonometric functions, focusing on the relationships between sine, cosine, and tangent in different quadrants. It explains how to use the unit circle to evaluate these functions and introduces the concept of reference angles. The script also covers the use of special triangles like 30-60-90 and 45-45-90 for simplifying trigonometric evaluations and discusses the limitations and applications of inverse trigonometric functions, providing a comprehensive guide for understanding and applying trigonometry.
Takeaways
- 📐 Understanding the unit circle is crucial for identifying the signs of trigonometric functions in different quadrants.
- 🧭 The first quadrant has all positive sine, cosine, and tangent functions, while the signs vary in the other quadrants based on the axis they are positive or negative on.
- 🔢 Memorizing the angles in radians corresponding to common degrees (30, 45, 60, etc.) is essential for trigonometry.
- 📈 The unit circle can be used to evaluate sine, cosine, and tangent functions by identifying the correct quadrant and using the associated XY coordinates.
- 🏹 Special triangles like the 30-60-90 and 45-45-90 are useful for evaluating trig functions without the unit circle.
- 🔄 Reference angles are key for evaluating trig functions of angles outside the first quadrant.
- 🌀 The signs of trigonometric functions in each quadrant can be remembered with the mnemonic: 'All Students Take Calculus In Quadrants One, Two, Three, and Four'.
- 🔢 The values of trig functions at specific angles (like sine of 30 is 1/2, cosine of 60 is 1/2) can be used to find the values of other functions at those angles using SOHCAHTOA.
- 🔄 To find the inverse of a trigonometric function, you must switch the roles of the angle and the value, but be aware of the restricted domains of inverse functions.
- 📊 The unit circle and special triangles are powerful tools for solving trigonometric problems and should be memorized for quick reference.
Q & A
What are the key points to remember about the unit circle and quadrants?
-The unit circle is a circle with a radius of 1 centered at the origin. In the first quadrant, all trigonometric functions (sine, cosine, tangent) are positive. Quadrant II is where sine is positive, and quadrant III is where tangent is positive. Quadrant IV has cosine as the positive function. The angles associated with the unit circle are 0, 30, 45, 60, 90, 120, 150, 180, 210, 225, 240, 270, 300, 315, 330, and 360 degrees, which correspond to 0, π/6, 5π/6, π/3, π/2, 2π/3, π, 3π/2, 4π/3, 5π/3, 6π/3, and 2π respectively in radians.
How can you determine the signs of trigonometric functions in different quadrants using the unit circle?
-In the unit circle, the signs of the trigonometric functions are determined by the quadrant in which the angle lies. In Quadrant I (0 to 90 degrees), all functions are positive. In Quadrant II (90 to 180 degrees), cosine is negative, and sine is positive. In Quadrant III (180 to 270 degrees), both sine and cosine are negative, but tangent is positive. In Quadrant IV (270 to 360 degrees), tangent is negative, and cosine is positive while sine is negative.
What is the significance of reference angles in trigonometry?
-Reference angles are the angles formed between the terminal side of an angle and the x-axis. They are used to find the values of trigonometric functions for angles that are not part of the special triangles (30-60-90 and 45-45-90). The reference angle is the acute angle formed, and it helps in determining the sign and value of the trigonometric functions based on the quadrant of the original angle.
How do you use the 30-60-90 triangle to evaluate trigonometric functions for angles not in the first quadrant?
-The 30-60-90 triangle can be used to find the values of trigonometric functions for angles outside the first quadrant by finding the reference angle and using the known ratios for the sides of the triangle. For example, sine 30 is 1/2, cosine 30 is √3/2, and tangent 30 is √3. These ratios can be applied to the reference angles in other quadrants, with adjustments for the signs based on the quadrant.
What is the relationship between the trigonometric functions and the sides of a right triangle?
-In a right triangle, the trigonometric functions are defined as follows: sine (θ) is the ratio of the length of the side opposite the angle θ to the length of the hypotenuse, cosine (θ) is the ratio of the length of the adjacent side to the length of the hypotenuse, and tangent (θ) is the ratio of the length of the opposite side to the length of the adjacent side.
How do you evaluate trigonometric functions for angles with negative degrees or radians?
-For negative angles, you first convert the negative angle to a positive coterminal angle by adding 360 degrees (or 2π radians) to the negative angle. Then, you find the trigonometric function values based on the coterminal positive angle and adjust the signs according to the quadrant in which the original negative angle lies. For example, tangent of a negative angle in the third quadrant will be negative, while cosine will be positive.
What are the restrictions on the domain of inverse trigonometric functions?
-The domain of inverse trigonometric functions is restricted based on the quadrant in which they are defined. For inverse sine (arcsin), the domain is between -90 and 90 degrees (or -π/2 to π/2 radians), and it only works for angles in the first and fourth quadrants. Inverse cosine (arccos) has a domain of 0 to 180 degrees (or 0 to π radians) and works for angles in the first and second quadrants. Inverse tangent (arctan) has a domain of -90 to 90 degrees (or -π/2 to π/2 radians) and works for angles in the first and fourth quadrants.
How do you find the values of other trigonometric functions if you know the value of sine for an angle in a specific quadrant?
-If you know the value of sine for an angle in a specific quadrant, you can use the Pythagorean theorem to find the missing sides of the right triangle formed by the unit circle. Once you have the lengths of the sides, you can calculate cosine as the adjacent side divided by the hypotenuse, tangent as the opposite side divided by the adjacent side, and so on for the other trigonometric functions.
What is the process for evaluating trigonometric functions for angles that are not part of special triangles?
-For angles that are not part of special triangles, you can use the unit circle to find the corresponding quadrant and then determine the signs of the trigonometric functions based on that quadrant. After that, you can either use the reference angle to find the values using the 30-60-90 or 45-45-90 triangles or use the inverse trigonometric functions to find the angle and then apply the trigonometric functions to that angle.
How do you evaluate the trigonometric functions for double angles using the information from a 3-4-5 triangle?
-For a double angle, you can use the double angle formulas. For sine double angle, it's 2sinθcosθ, and for cosine double angle, it's cos²θ - sin²θ. Using the 3-4-5 triangle, where sinθ = 3/5 and cosθ = 4/5, you can calculate sin(2θ) as 2*(3/5)*(4/5) = 24/25 and cos(2θ) as (4/5)² - (3/5)² = -7/25.
What are the key differences between the trigonometric functions and their reciprocals?
-The reciprocals of the trigonometric functions are known as the cosecant (csc), secant (sec), and cotangent (cot). Cosecant is the reciprocal of sine (csc(θ) = 1/sin(θ)), secant is the reciprocal of cosine (sec(θ) = 1/cos(θ)), and cotangent is the reciprocal of tangent (cot(θ) = 1/tan(θ)). These reciprocal functions have different signs in different quadrants and are used in various trigonometric identities and equations.
Outlines
📚 Introduction to the Unit Circle and Quadrants
This paragraph introduces the concept of the unit circle and its significance in understanding trigonometric functions. It explains the four quadrants and their association with the signs of sine, cosine, and tangent functions. The paragraph also covers the importance of knowing angles in radians and their corresponding values on the unit circle, such as 30, 45, 60, 120, and 330 degrees, and their relationships to the reference angles of 30, 45, and 60 degrees.
📈 Trigonometric Values on the Unit Circle
The paragraph delves into the specific values of trigonometric functions on the unit circle for various angles. It discusses how to determine the X and Y coordinates for angles in different quadrants and how these values change based on the quadrant's characteristics. The explanation includes how to evaluate sine, cosine, and tangent for angles like 60, 120, 240, and 330 degrees using the unit circle and the significance of reference angles in determining the sign of these functions.
🔢 Evaluating Trigonometric Functions without the Unit Circle
This section provides techniques for evaluating trigonometric functions without relying on the unit circle. It introduces the 30-60-90 and 45-45-90 triangles, explaining their side ratios and how to use them to find sine, cosine, and tangent values for specific angles. The paragraph also discusses the concept of reference angles and how they can be used to evaluate functions for angles not within the special triangles.
🤔 Handling Trigonometric Functions with Special Angles
The paragraph focuses on how to handle trigonometric functions for angles that are not part of the special triangles. It explains the concept of reference angles and how to use them to find the values of sine, cosine, and tangent for angles like 120 and 240 degrees. The explanation includes converting angles to their reference angles and applying the correct sign based on the quadrant in which the angle resides.
📊 Evaluating Trigonometric Functions for Larger Angles
This section discusses the evaluation of trigonometric functions for larger angles that are not within the first 360 degrees. It explains how to find coterminal angles and use them to determine the trigonometric values. The paragraph covers the evaluation of tangent, cosine, and secant for angles like 330 and 225 degrees, emphasizing the importance of understanding the quadrant and the reference angle in determining the sign and value of the functions.
🔄 Understanding Inverse Trigonometric Functions
The paragraph introduces inverse trigonometric functions, explaining the concept and how to use them to find angles based on given function values. It highlights the restricted domains of inverse sine, inverse cosine, and inverse tangent, and how these limitations affect the possible angles that can be found using inverse functions. The explanation includes examples of how to correctly apply inverse functions and the importance of considering the quadrant and angle range when solving for the angle.
📐 Applying Inverse Trigonometric Functions
This section provides a practical application of inverse trigonometric functions, demonstrating how to find angles when given the value of sine, cosine, or tangent. It emphasizes the importance of understanding the restricted domains of inverse functions and how to correctly identify the quadrant and angle range when solving for the angle. The paragraph includes examples of finding inverse cosine and inverse tangent for specific values, highlighting the need to consider the quadrant in which the angle lies.
Mindmap
Keywords
💡Unit Circle
💡Quadrants
💡Trigonometric Functions
💡Reference Angle
💡Soh-Cah-Toe-A
💡Inverse Trigonometric Functions
💡Special Triangles
💡Rationalizing Denominators
💡Coterminal Angles
💡Trigonometric Identities
Highlights
The unit circle is the focus of the video, which is essential in understanding trigonometric functions.
Quadrant knowledge is crucial for determining the signs of sine, cosine, and tangent functions.
The association of cosine with the x-value and sine with the y-value is fundamental in trigonometry.
Memory aids like 'all students take calculus in quadrant one' help in remembering the positivity of functions.
The angles 30, 45, 60, 120, 150, 210, 225, 300, and 330 degrees have specific radian equivalents.
The unit circle provides XY coordinates for these key angles, which are vital for evaluating trig functions.
The signs of trigonometric function values change depending on the quadrant, which is a critical concept.
The video explains how to use the unit circle to evaluate sine, cosine, and tangent functions.
The 30-60-90 and 45-45-90 triangles are introduced as tools for evaluating trig functions without the unit circle.
The concept of reference angles is introduced to evaluate trig functions for angles not in the first quadrant.
The video demonstrates how to evaluate trig functions for angles in different quadrants using the unit circle and reference angles.
Inverse trigonometric functions are discussed, with emphasis on their restricted domains.
The video provides examples of how to find the other trig functions if one is given, like cosine or tangent.
The process of evaluating trig functions using the Pythagorean theorem and special triangles is explained.
Double angle formulas for sine and cosine are introduced, along with how to evaluate them using the unit circle.
The video concludes with a discussion on the limitations of inverse functions and their domains.
Transcripts
Browse More Related Video

How To Find The Exact Values of Trig Functions
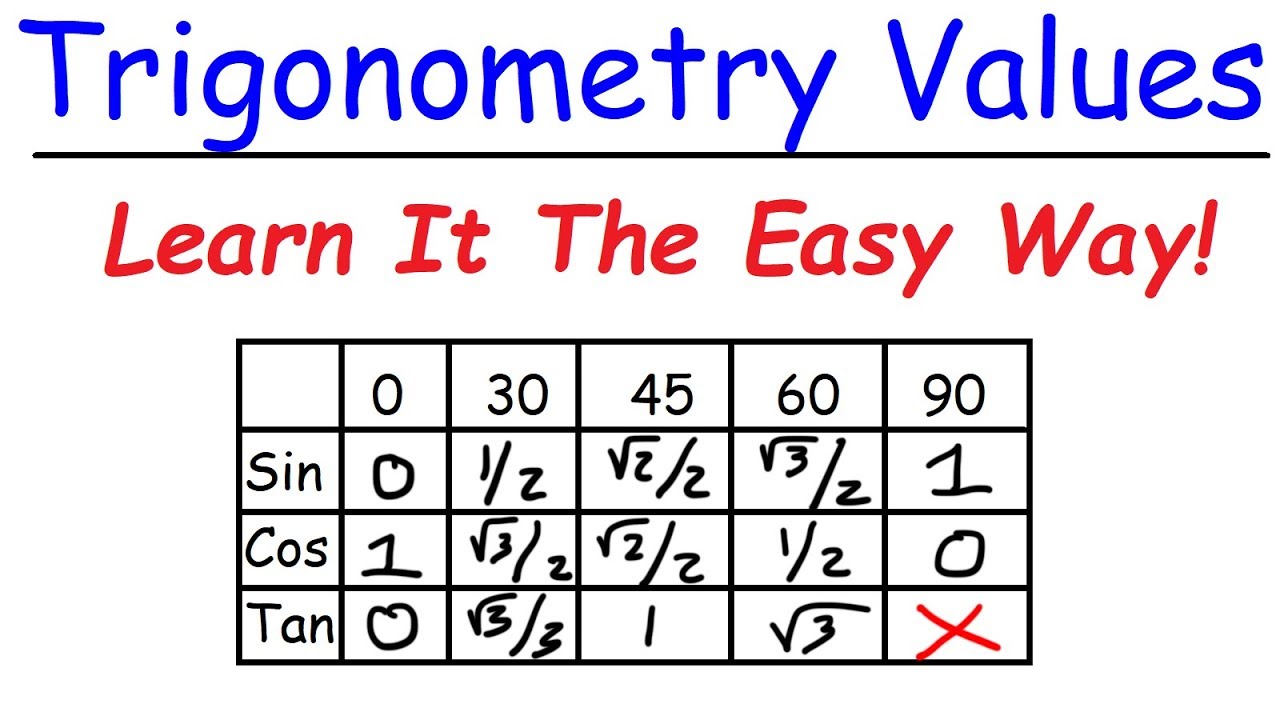
A Simple Trick To Remember Trigonometry Values
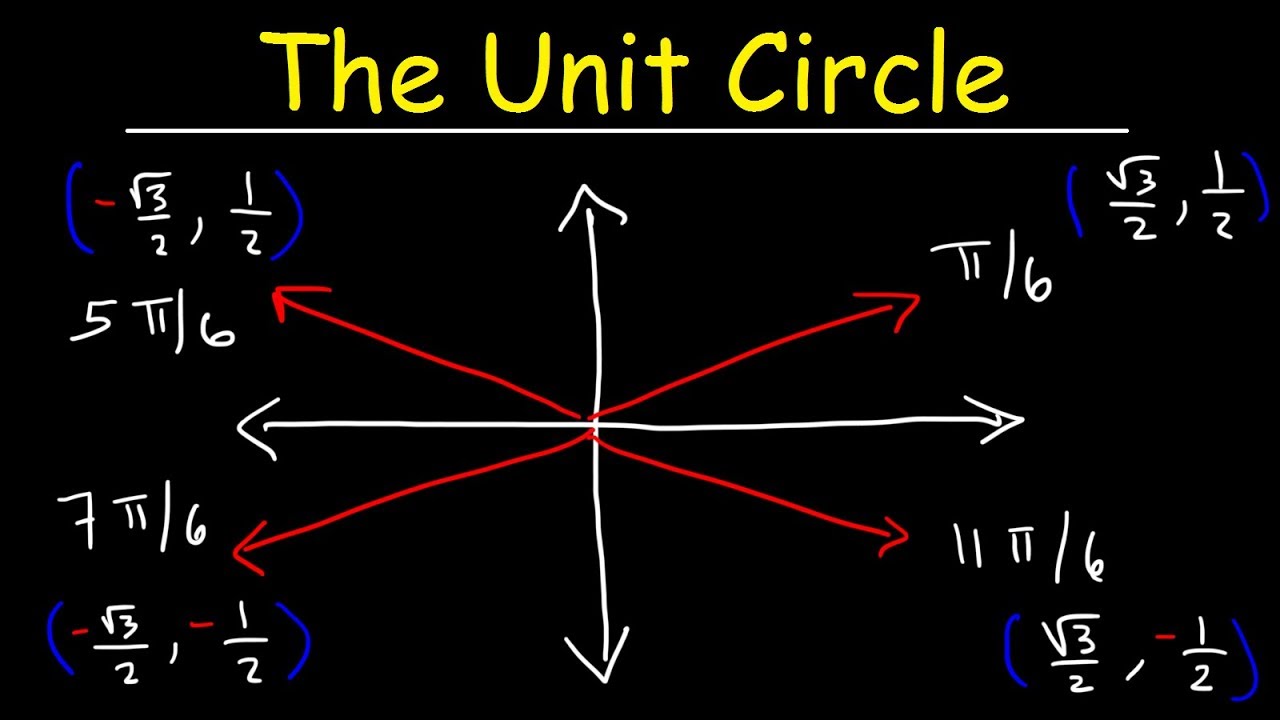
The Unit Circle, Basic Introduction, Trigonometry

30-60-90 Triangles - Special Right Triangle Trigonometry
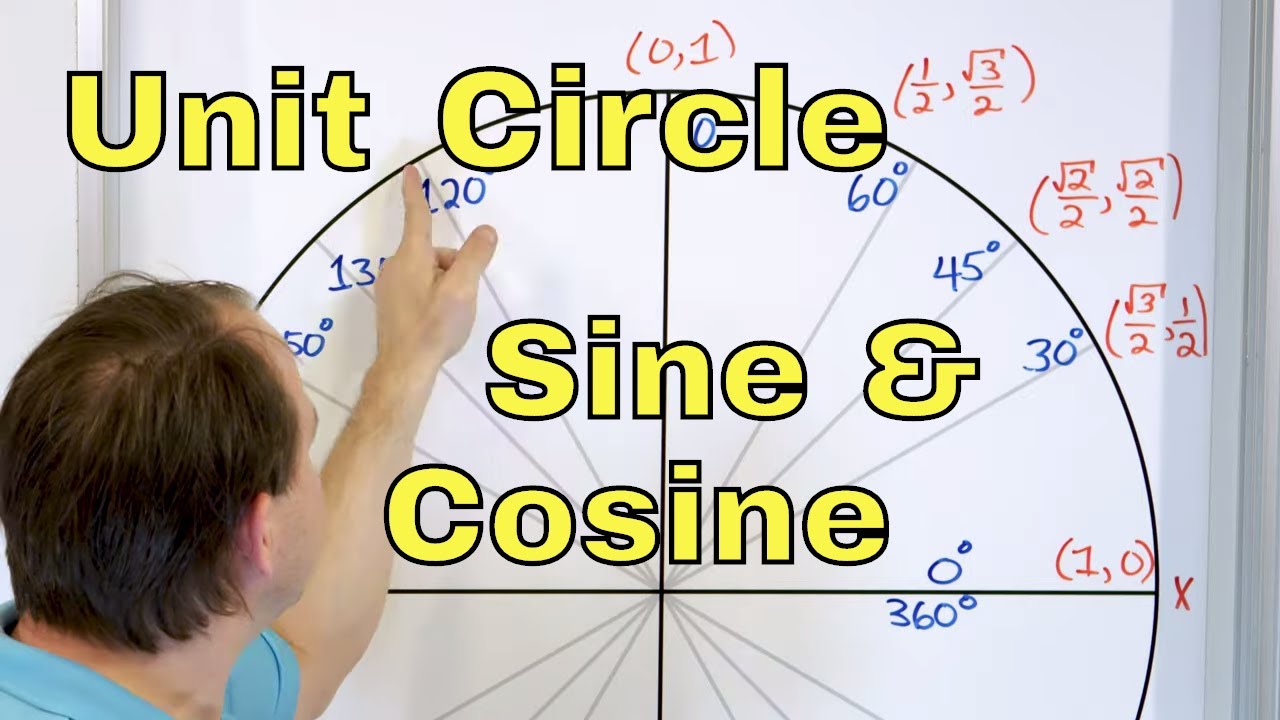
09 - Unit Circle - Definition & Meaning - Sin(x), Cos(x), Tan(x), - Sine, Cosine & Tangent

How To Use Reference Angles to Evaluate Trigonometric Functions
5.0 / 5 (0 votes)
Thanks for rating: