How To Find The Exact Values of Trig Functions

The Organic Chemistry Tutor
28 Jun 202012:39
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script offers a comprehensive guide on determining the exact values of trigonometric functions, focusing on special right triangles like the 30-60-90 and 45-45-90. It introduces the mnemonic SOHCAHTOA for sine, cosine, and tangent ratios and demonstrates step-by-step calculations for various angles in degrees and radians. The script also covers converting angles to their reference angles and understanding the impact of different quadrants on the signs of trigonometric values. With clear examples, it simplifies the process of finding exact trigonometric values, making it accessible for learners.

Takeaways
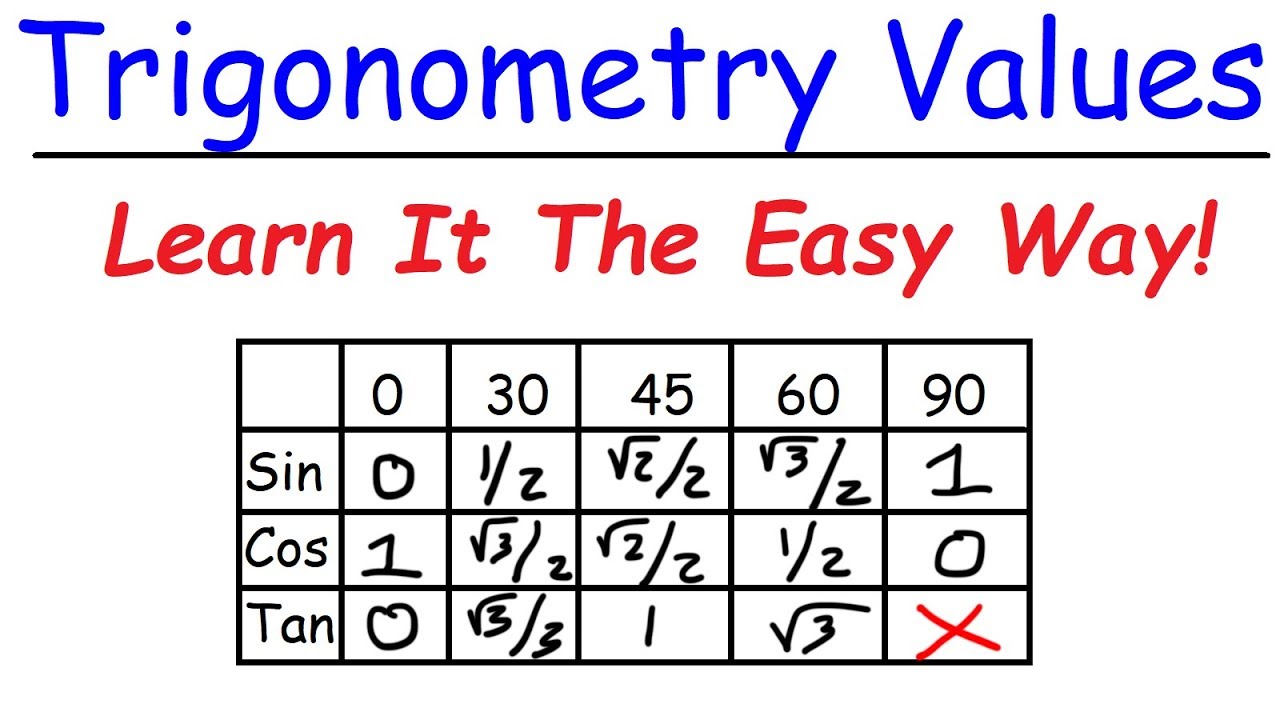
  • πŸ“ Familiarize with the 30-60-90 triangle where the side across the 30 degree angle is 1, the side across the 60 degree angle is the square root of 3, and the hypotenuse is 2.
  • πŸ“ Understand the 45-45-90 triangle where the sides across the 45 degree angles are equal to 1 and the hypotenuse is the square root of 2.
  • πŸ“š Learn SOHCAHTOA mnemonic for sine, cosine, and tangent ratios to find the exact values of trigonometric functions.
  • πŸ” To find sine 30 degrees, use the formula sine = opposite/hypotenuse, with the opposite side being 1 and the hypotenuse being 2, resulting in sine 30 degrees being one over two.
  • πŸ”’ Convert radians to degrees by multiplying the radian measure by 180/pi to work with degree measures.
  • πŸ“ For angles not directly given in special triangles, plot the angle and create a reference triangle to find trigonometric values.
  • πŸ“Š Recognize that cosine of an angle in a specific quadrant can be found by considering the reference angle and the signs of the sides in that quadrant.
  • πŸ“‰ For tangent, rationalize the denominator to simplify the expression and find the exact value.
  • πŸ”„ Remember that angles can be coterminal, meaning they share the same terminal side but have different angle measures; adjust by subtracting or adding multiples of 360 degrees.
  • πŸ“ When dealing with negative angles, move clockwise from the positive x-axis to create a reference triangle and find the trigonometric values.
  • πŸ“˜ Summarize that to find the exact value of trigonometric functions, one must understand special triangles, convert angles appropriately, and apply the correct trigonometric ratios while considering the signs in different quadrants.
Q & A

  • What are the side ratios in a 30-60-90 right triangle?

    -In a 30-60-90 triangle, the side across the 30-degree angle is 1, the side across the 60-degree angle is the square root of 3, and the hypotenuse is 2.

  • What is the significance of the 45-45-90 triangle in trigonometry?

    -The 45-45-90 triangle is significant because the sides opposite the 45-degree angles are equal in length, and the hypotenuse is √2 times the length of the other two sides.

  • What does SOHCAHTOA represent in trigonometry?

    -SOHCAHTOA is a mnemonic used to remember the sine, cosine, and tangent ratios in right triangles: Sine (opposite/hypotenuse), Cosine (adjacent/hypotenuse), and Tangent (opposite/adjacent).

  • How do you find the exact value of sine for a 30-degree angle?

    -To find the exact value of sine for a 30-degree angle, use the formula sine = opposite/hypotenuse. In the 30-60-90 triangle, the opposite side to 30 degrees is 1 and the hypotenuse is 2, so sine 30 degrees is 1/2.

  • How can you convert an angle from radians to degrees?

    -To convert an angle from radians to degrees, multiply the radian measure by 180 and divide by pi (Ο€). Since Ο€ equals 180 degrees, the Ο€ unit cancels out, leaving you with just the degree measure.

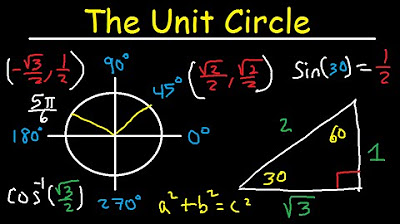
  • What is the reference angle for 150 degrees?

    -The reference angle for 150 degrees is 30 degrees because 150 degrees is 30 degrees away from the negative x-axis (180 degrees).

  • How do you determine the sign of trigonometric functions in different quadrants?

    -In quadrant I, all trigonometric functions are positive. In quadrant II, cosine is negative while sine is positive. In quadrant III, both sine and cosine are negative. In quadrant IV, tangent is negative while sine and cosine are positive.

  • What is the exact value of cosine for 150 degrees?

    -The exact value of cosine for 150 degrees is -√3/2. This is because cosine is the adjacent side over the hypotenuse in a right triangle, and in quadrant II, the adjacent side to the reference angle of 30 degrees is -√3, and the hypotenuse is 2.

  • How do you rationalize the denominator of a fraction involving a square root?

    -To rationalize the denominator, multiply both the numerator and the denominator by the square root that is present in the denominator. This will eliminate the square root from the denominator.

  • What is the process for finding the exact value of tangent for an angle of Ο€/6 radians?

    -First, convert Ο€/6 radians to degrees by multiplying Ο€ by 180 and dividing by 6, which gives 30 degrees. Then, use the tangent ratio (opposite/adjacent) for a 30-degree angle, which is 1/√3. Rationalize the denominator by multiplying by √3/√3, resulting in the exact value of tangent 30 degrees being √3/3.

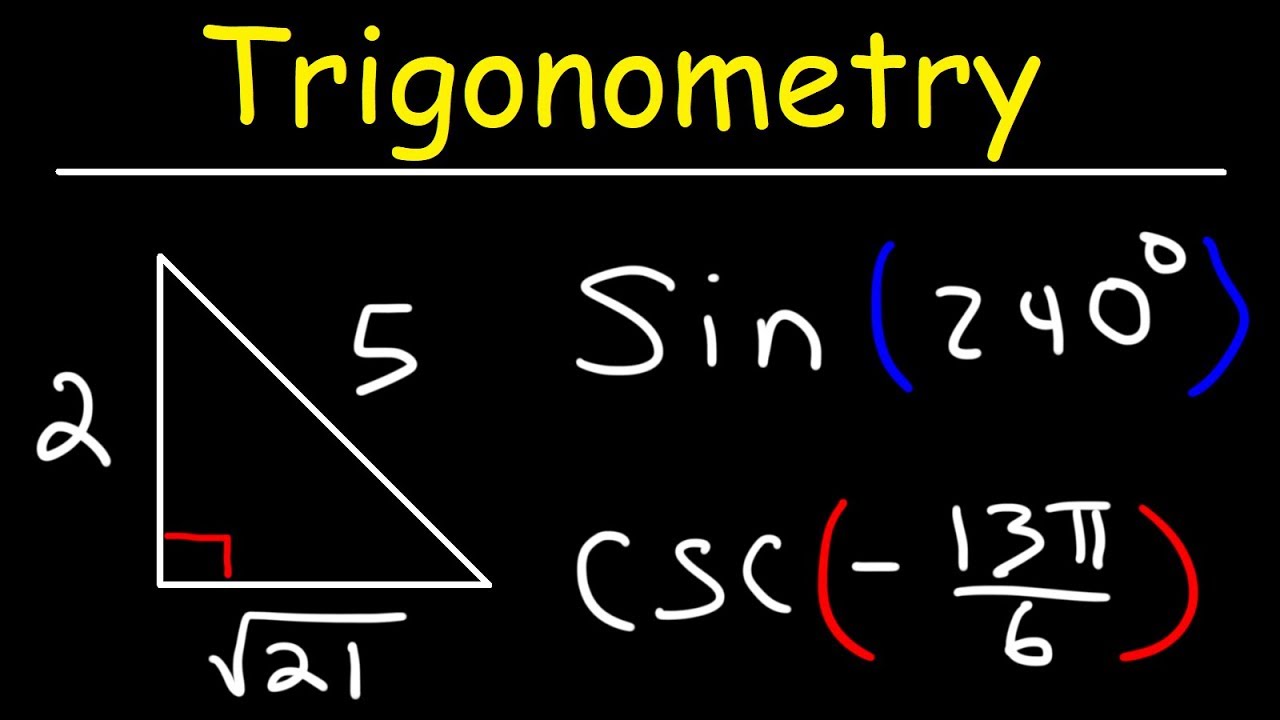
  • What is the reference angle for 240 degrees?

    -The reference angle for 240 degrees is 60 degrees because 240 degrees is 60 degrees away from the 180 degrees line.

  • How do you find the exact value of cosine for 240 degrees?

    -The exact value of cosine for 240 degrees is -1/2. This is found by using the cosine ratio (adjacent/hypotenuse) for the reference angle of 60 degrees in quadrant III, where the adjacent side is -1 and the hypotenuse is 2.

  • What is the process for finding the exact value of sine for an angle of 10Ο€/3 radians?

    -First, convert 10Ο€/3 radians to degrees by multiplying 10 by 60, which gives 600 degrees. Since 600 degrees is coterminal with 240 degrees, find the sine for the reference angle of 60 degrees in quadrant III. The exact value of sine for 10Ο€/3 radians is -√3/2, using the sine ratio (opposite/hypotenuse) where the opposite side is -√3 and the hypotenuse is 2.

  • What is the reference angle for a negative angle, and how do you find it?

    -The reference angle for a negative angle is the positive angle you would measure in the clockwise direction from the positive x-axis. To find it, draw the angle clockwise from the positive x-axis and determine the smallest angle it makes with the x-axis.

  • How do you find the exact value of tangent for a negative angle of -45 degrees?

    -The exact value of tangent for -45 degrees is -1. This is because, in quadrant IV, the x-axis is positive and the y-axis is negative, making the tangent (opposite/adjacent) equal to -1/1.

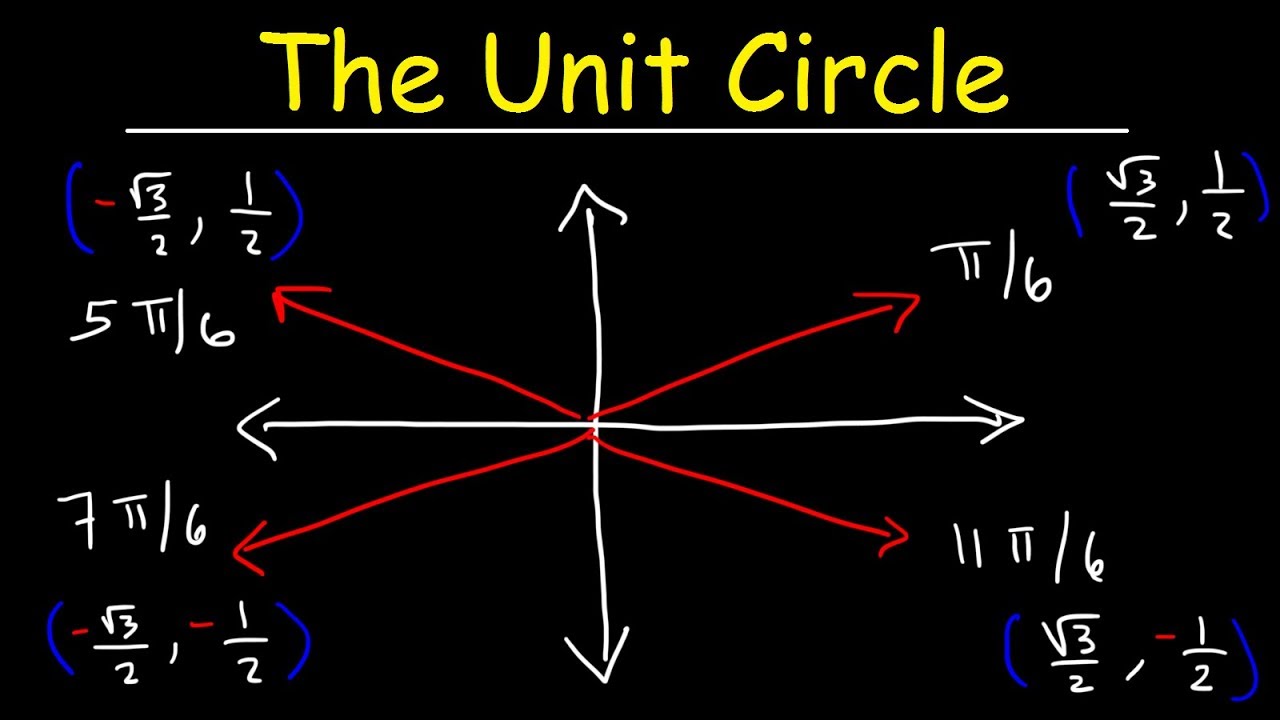
  • What are coterminal angles, and how do you find them?

    -Coterminal angles are angles that share the same terminal side. To find a coterminal angle, subtract or add multiples of 360 degrees to an angle until you get an angle between 0 and 360 degrees for positive angles, or add multiples of 360 degrees to a negative angle until it falls between 0 and 360 degrees.

Outlines
00:00
πŸ“š Introduction to Trigonometry with Special Triangles

This paragraph introduces the topic of finding the exact values of trigonometric functions, focusing on the 30-60-90 and 45-45-90 right triangles. It explains the side ratios in these triangles and introduces the acronym SOHCAHTOA to remember the sine, cosine, and tangent ratios. The paragraph demonstrates how to use these concepts to find the sine of 30 degrees, using the 30-60-90 triangle and the SOHCAHTOA rule, resulting in the exact value of one over two.

05:03
πŸ“ Converting Radians to Degrees and Evaluating Trigonometric Functions

This paragraph continues the discussion on trigonometric functions by showing how to convert an angle from radians to degrees, using the example of cosine 5Ο€/6. It explains the process of converting the angle to 150 degrees and then creating a reference triangle to find the exact value. The paragraph covers how to determine the signs of the trigonometric functions based on the quadrant and uses the SOHCAHTOA rule to find the exact value of cosine 150 degrees, which is negative square root of 3 over 2. It also includes an example of finding the tangent of Ο€/6, rationalizing the denominator to get the final value.

10:04
πŸ“‰ Evaluating Trigonometric Functions for Various Angles

The final paragraph discusses the process of evaluating trigonometric functions for different angles, such as cosine 240 degrees and tangent of negative 45 degrees. It describes how to draw reference triangles and determine the signs based on the quadrant. The paragraph explains that cosine 240 degrees is equivalent to cosine 60 degrees in quadrant 3, resulting in negative one-half. For tangent of negative 45 degrees, it shows that the function equals -1. Additionally, it covers the concept of coterminal angles, explaining how to adjust large or negative angles to find their equivalent between 0 and 360 degrees. The paragraph concludes with finding the sine of 10Ο€/3, which is equivalent to sine of 240 degrees, resulting in negative square root of 3 over 2.

Mindmap
Keywords
πŸ’‘Trigonometric functions
Trigonometric functions are mathematical functions that relate the angles of a triangle to the lengths of its sides. In the context of the video, these functions are sine, cosine, and tangent, which are used to find the ratios of sides in right-angled triangles. The video's theme revolves around finding the exact values of these functions using special triangles and angle conversions.
πŸ’‘30-60-90 triangle
A 30-60-90 triangle is a right-angled triangle where the angles are 30 degrees, 60 degrees, and 90 degrees. The sides are in the ratio of 1:√3:2, with the hypotenuse being twice as long as the shortest side. The video uses this special triangle to demonstrate how to find the sine, cosine, and tangent of a 30-degree angle.
πŸ’‘45-45-90 triangle
A 45-45-90 triangle, also known as an isosceles right triangle, has two 45-degree angles and a 90-degree angle. The sides opposite the 45-degree angles are of equal length, and the hypotenuse is √2 times the length of the shorter sides. The video mentions this triangle as one of the special triangles to be familiar with for solving trigonometric problems.
πŸ’‘SOHCAHTOA
SOHCAHTOA is a mnemonic used to remember the trigonometric ratios: sine (opposite/hypotenuse), cosine (adjacent/hypotenuse), and tangent (opposite/adjacent). The video explains how to use this mnemonic to find the sine, cosine, and tangent of specific angles by relating them to the sides of right-angled triangles.
πŸ’‘Radians to degrees
Radians and degrees are two units for measuring angles. Radians are often used in calculus and other advanced mathematics, while degrees are more common in basic trigonometry. The video demonstrates how to convert from radians to degrees by multiplying the radian measure by 180/Ο€, which is necessary to use the special triangles for finding trigonometric values.
πŸ’‘Reference angle
A reference angle is the acute angle formed between the terminal side of an angle and the x-axis in standard position. The video explains how to find the reference angle for angles greater than 90 degrees or negative angles and how to use it to determine the trigonometric values in different quadrants.
πŸ’‘Quadrants
In the context of the video, quadrants refer to the four sections created by the x and y axes on a Cartesian plane. Each quadrant has specific signs for the x and y coordinates: first quadrant (+,+), second quadrant (-,+), third quadrant (-,-), and fourth quadrant (+,-). The video uses quadrants to determine the signs of the trigonometric functions.
πŸ’‘Rationalizing the denominator
Rationalizing the denominator is a mathematical process used to eliminate square roots from the denominator of a fraction. In the video, this concept is used when finding the tangent of Ο€/6 radians, where the denominator is multiplied by √3 to obtain a rationalized form.
πŸ’‘Coterminal angles
Coterminal angles are angles that share the same terminal side when drawn on a circle. The video explains that angles are coterminal if they differ by full rotations (multiples of 360 degrees). This concept is used to simplify finding the sine of large or negative angles by reducing them to an equivalent angle between 0 and 360 degrees.
πŸ’‘Exact values
Exact values in trigonometry refer to the precise numerical values of trigonometric functions for specific angles. The video's main theme is finding these exact values using special triangles and angle properties, providing examples such as sine 30Β°, cosine 150Β°, and tangent 30Β°.
Highlights

Introduction to finding the exact value of trigonometric functions using special right triangles.

Explanation of the 30-60-90 triangle properties with sides in the ratio 1:√3:2.

Introduction to the 45-45-90 triangle with equal sides opposite to the 45-degree angles and hypotenuse in the ratio 1:1:√2.

Explanation of SOHCAHTOA mnemonic for sine, cosine, and tangent ratios.

Demonstration of finding the exact value of sine 30 degrees using the 30-60-90 triangle.

Conversion of radian measure to degrees by multiplying by 180/pi.

Method to evaluate cosine 150 degrees by creating a reference triangle.

Incorporation of negative signs in trigonometric functions based on quadrant.

Calculation of cosine 5Ο€/6 radians (150 degrees) using the reference triangle.

Conversion of pi/6 radians to 30 degrees and finding the tangent of 30 degrees.

Rationalization of the denominator in the tangent function.

Drawing a reference triangle to find cosine 240 degrees.

Understanding the properties of cosine in quadrant 3 to find cosine 240 degrees.

Approach to finding the tangent of negative 45 degrees using a reference triangle.

Explanation of coterminal angles and their significance in trigonometry.

Conversion of sine 10Ο€/3 radians to sine 240 degrees and finding its value.

Final summary on how to find the exact value of trigonometric functions using special triangles and reference angles.

Transcripts

Browse More Related Video

How To Use Reference Angles to Evaluate Trigonometric Functions

A Simple Trick To Remember Trigonometry Values

Unit Circle Trigonometry - Sin Cos Tan - Radians & Degrees

Trigonometry

The Unit Circle, Basic Introduction, Trigonometry

Trigonometry Final Exam Review

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
TrigonometryExact ValuesSpecial TrianglesSOHCAHTOA30-60-9045-45-90Radians to DegreesReference AnglesTrig FunctionsMathematics EducationGeometry