The Unit Circle, Basic Introduction, Trigonometry

The Organic Chemistry Tutor
12 Oct 201712:48
EducationalLearning
32 Likes 10 Comments

TLDRThis educational script delves into the concept of the unit circle, a fundamental tool in trigonometry with a radius of one. It explains how to use the unit circle to determine sine and cosine values for various angles, focusing on common angles like 30, 45, and 60 degrees. The script also illustrates how to find trigonometric values for angles not directly on the unit circle by utilizing symmetry and reference angles. It guides through examples, demonstrating how to evaluate sine and cosine for angles like 135, 225, and 315 degrees, and extends the explanation to angles in radians, such as pi/3, 2pi/3, and so on. The key takeaway is that memorizing quadrant one values and understanding the unit circle's symmetry allows for easy evaluation of trigonometric functions across all quadrants.

Takeaways
  • πŸ“ The unit circle is a circle with a radius of one, where the hypotenuse of a 45-degree angle triangle equals 1.
  • πŸ“ˆ At a 45-degree angle, the x and y values of the triangle are equal, resulting in the point at (√2, 2).
  • 🧭 Sine of an angle (ΞΈ) is the y-value of the point on the unit circle, while cosine (ΞΈ) is the x-value.
  • πŸ”’ For the unit circle, sine 45 degrees equals y-coordinate (√2/2), and cosine 45 degrees equals x-coordinate (√2/2).
  • πŸ“Š Three common angles to know on the unit circle in quadrant one are 30, 45, and 60 degrees, each with specific x and y values.
  • πŸ“ At 30 degrees, x is √3/2 and y is 1/2; at 60 degrees, x is 1/2 and y is √3/2.
  • πŸ”„ Values at 0 and 90 degrees are (1,0) and (0,1) respectively, and at 180 and 270 degrees, the signs of x and y values change accordingly.
  • πŸ”’ To find sine or cosine of other angles, use the symmetry of the unit circle and the values from quadrant one.
  • πŸ“ For angles not in the first quadrant, determine the reference angle and adjust the sign based on the quadrant.
  • πŸ“š Memorizing the unit circle or understanding its symmetry can help evaluate sine and cosine functions for any angle.
  • πŸ“˜ Examples are provided to demonstrate how to find the values of sine and cosine for various angles using the unit circle.
Q & A

  • What is a unit circle?

    -A unit circle is a circle with a radius of one. It is used in trigonometry to define and evaluate sine and cosine values based on angles.

  • How is the unit circle used to find the sine of 45 degrees?

    -To find the sine of 45 degrees, you look at the y-coordinate of the point on the unit circle that corresponds to a 45-degree angle. In this case, it is the square root of 2 divided by 2.

  • What are the x and y values of a point on the unit circle at a 30-degree angle?

    -At a 30-degree angle, the x value is root three over two, and the y value is one over two.

  • How do you determine the cosine of an angle using the unit circle?

    -The cosine of an angle is equal to the x value of the terminal point on the unit circle corresponding to that angle.

  • What are the coordinates of the point on the unit circle at a 60-degree angle?

    -At a 60-degree angle, the x value is one half, and the y value is root three over two.

  • How can you find the sine and cosine values for angles not in the first quadrant using the unit circle?

    -You can find the sine and cosine values for other quadrants by using the reference angle (the acute angle) and knowing the sign of the x and y values based on the quadrant.

  • What is the sine of 135 degrees?

    -The sine of 135 degrees is the same as the sine of 45 degrees but with the opposite sign in the second quadrant, so it is positive square root of 2 divided by 2.

  • What is the cosine of 180 degrees?

    -The cosine of 180 degrees is -1, as the x value for the point on the unit circle at 180 degrees is -1.

  • How do you find the sine of 315 degrees?

    -The sine of 315 degrees is the y value of the point on the unit circle at that angle, which is negative root two over two in the fourth quadrant.

  • What is the process for finding the trigonometric values for angles in radians using the unit circle?

    -To find trigonometric values in radians, you first convert the angle to degrees if necessary, then find the corresponding x and y values on the unit circle for that angle, and use the quadrant to determine the correct sign for the sine and cosine values.

Outlines
00:00
πŸ“š Understanding the Unit Circle and Trigonometric Functions

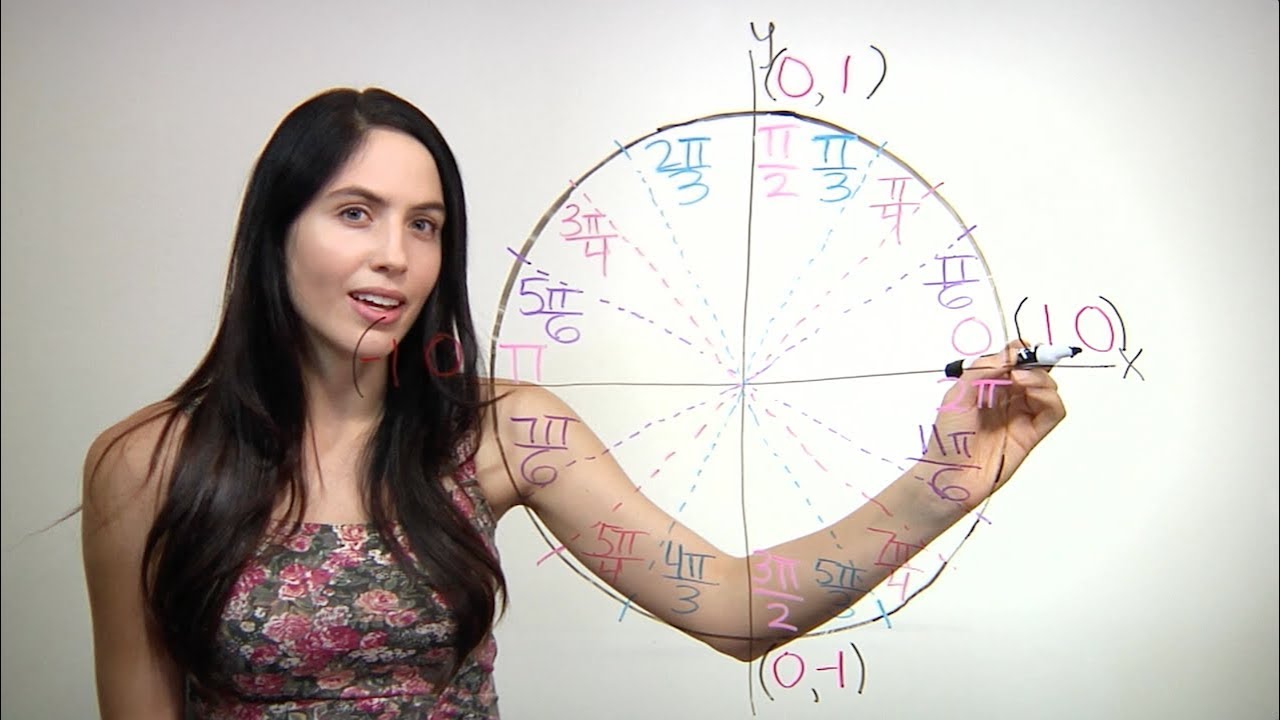
This paragraph introduces the concept of the unit circle, which is a circle with a radius of one. It explains how the unit circle can be used to determine the sine and cosine values for certain angles, specifically focusing on the angles of 30, 45, and 60 degrees in the first quadrant. The paragraph illustrates that at a 45-degree angle, the x and y coordinates are equal, both being \( \sqrt{2}/2 \), and that these coordinates represent the sine and cosine values respectively for that angle. It also mentions the values at 0, 90, 180, and 270 degrees, emphasizing the symmetry of the unit circle and how it can be used to find sine and cosine values for other angles by understanding the first quadrant and the coordinate axes.

05:00
πŸ” Evaluating Trigonometric Functions Using the Unit Circle

The second paragraph delves into how to find sine and cosine values for angles not initially covered, such as 135, 225, and 315 degrees, by using the symmetry of the unit circle and the knowledge of the first quadrant. It explains that for angles like 135 and 225 degrees, which have a reference angle of 45 degrees, the sine and cosine values are the same in magnitude as those at 45 degrees but with opposite signs depending on the quadrant. The paragraph also covers how to determine the values for angles in radians, specifically pi/3 (60 degrees), 2pi/3, 4pi/3, and 5pi/3, by understanding the reference angle and the signs of the coordinates in different quadrants.

10:01
πŸ“‰ Applying Unit Circle Knowledge to Find Trigonometric Values

The final paragraph provides a practical application of the unit circle by guiding the viewer to find the values of sine and cosine for various angles expressed in radians, specifically pi/6, 5pi/6, 7pi/6, and 11pi/6, which correspond to 30, 150, 210, and 330 degrees respectively. It explains the signs of the sine and cosine values based on the quadrant in which each angle lies and provides the actual values for these trigonometric functions at the specified angles. The paragraph reinforces the idea that knowledge of the unit circle allows for the easy evaluation of trigonometric functions without memorization of each individual angle.

Mindmap
Keywords
πŸ’‘Unit Circle
A unit circle is a circle with a radius of one. It is a fundamental concept in trigonometry, used to define the trigonometric functions for all angles. In the video, the unit circle serves as the basis for explaining sine and cosine values at various angles, such as 45 degrees and 60 degrees, by identifying the coordinates of points on the circle.
πŸ’‘Sine
Sine is a trigonometric function that relates the ratio of the length of the side opposite an angle to the length of the hypotenuse in a right-angled triangle. In the context of the unit circle, sine corresponds to the y-coordinate of a point on the circle, which represents the output of the sine function for a given angle. For example, the sine of 45 degrees is the y-coordinate of the point associated with a 45-degree angle on the unit circle, which is \(\sqrt{2}/2\).
πŸ’‘Cosine
Cosine is another trigonometric function that relates to the ratio of the length of the adjacent side to the hypotenuse in a right-angled triangle. On the unit circle, cosine is represented by the x-coordinate of a point on the circle. It is used to find the cosine of an angle by identifying the x-coordinate of the corresponding point. For instance, the cosine of 180 degrees is the x-coordinate of the point at 180 degrees on the unit circle, which is -1.
πŸ’‘Reference Angle
A reference angle is the acute angle formed by the terminal side of an angle and the x-axis. It is used to determine the trigonometric values for angles outside the first quadrant by using the symmetry of the unit circle. The video explains that angles like 135 degrees and 225 degrees have a reference angle of 45 degrees, which helps in finding their sine and cosine values.
πŸ’‘Quadrant
A quadrant refers to one of the four equal parts of a plane that is divided by the two axes (x and y). Quadrants are numbered counterclockwise, starting from the upper right as the first quadrant. In the video, the concept of quadrants is used to explain how the signs of sine and cosine change depending on the quadrant in which the angle lies, with sine being positive in the first and second quadrants and cosine being positive in the first and fourth quadrants.
πŸ’‘Radians
Radians are a unit of angular measure where an angle of one radian subtends an arc of the circle's radius. The video script converts degrees to radians to explain trigonometric functions, such as pi over 3 radians, which corresponds to 60 degrees. This conversion is crucial for understanding the relationship between angles and their trigonometric values on the unit circle.
πŸ’‘Hypotenuse
The hypotenuse is the longest side of a right-angled triangle, opposite the right angle. In the context of the unit circle, when a ray is drawn at a 45-degree angle, the hypotenuse of the resulting triangle is equal to the radius of the unit circle, which is one. This is used to explain why the x and y values of the triangle are equal and both are \(\sqrt{2}/2\).
πŸ’‘Symmetry
Symmetry in the unit circle refers to the predictable patterns of sine and cosine values based on the angle's quadrant. The video emphasizes that knowing the values in the first quadrant and the signs of the coordinates on the x and y axes allows one to determine the trigonometric values for all other angles by using symmetry. For example, the sine of 135 degrees is the same as the sine of 45 degrees but with a negative x-coordinate.
πŸ’‘Trigonometric Functions
Trigonometric functions are mathematical functions that relate the angles of a triangle to the lengths of its sides. In the video, sine and cosine are the primary trigonometric functions discussed, which are evaluated using the unit circle. These functions are essential for solving various problems in mathematics, physics, and engineering.
πŸ’‘Coordinate System
A coordinate system is a framework that uses ordered pairs of numbers, called coordinates, to uniquely determine the position of points. In the video, the Cartesian coordinate system is used to describe the points on the unit circle, where the x and y values of these points correspond to the cosine and sine of the angle, respectively.
Highlights

The unit circle is a circle with a radius of one.

At a 45-degree angle, the x and y values of the unit circle are equal, resulting in the point at (√2/2, √2/2).

Sine of an angle is the y value of the corresponding point on the unit circle, and cosine is the x value.

Sine 45 degrees is equal to the y coordinate of the point associated with 45 degrees, which is √2/2.

Common values on the unit circle in quadrant one include 30, 45, and 60 degrees.

At a 30-degree angle, the x value is √3/2 and the y value is 1/2.

At a 60-degree angle, the x value is 1/2 and the y value is √3/2.

Values at 0 and 90 degrees are (1,0) and (0,1) respectively, and at 180 and 270 degrees are (-1,0) and (0,-1).

Sine 60 degrees is √3/2, cosine 180 degrees is -1, and sine 30 degrees is 1/2.

Angles 135, 225, and 315 degrees can be found using the symmetry of the unit circle and the first quadrant values.

Sine 135 degrees is positive √2/2, as it shares the same reference angle as 45 degrees but with a negative x value.

Cosine 225 degrees is negative √2/2, reflecting the negative x value in quadrant two.

Sine 315 degrees is negative √2/2, with a positive x value in quadrant four but a negative y value.

Knowing the first quadrant and the x and y axis values allows you to determine all other angles on the unit circle.

Sine and cosine values can be found for angles in radians, such as pi/3, 2pi/3, 4pi/3, and 5pi/3.

At pi/3 or 60 degrees, the unit circle point is (1/2, √3/2), which helps find values for other related angles.

Sine pi/3 is √3/2, cosine 2pi/3 is -1/2, sine 4pi/3 is -√3/2, and cosine 5pi/3 is 1/2.

Angles pi/6, 5pi/6, 7pi/6, and 11pi/6 correspond to 30, 150, 210, and 330 degrees respectively.

Sine pi/6 or sine 30 is 1/2, cosine 5pi/6 is -√3/2, cosine 7pi/6 is -√3/2, and sine 11pi/6 is -1/2.

Transcripts

Browse More Related Video

How to Remember the Unit Circle (NancyPi)

Reciprocal Identities - Evaluating Secant and Cosecant Functions

30-60-90 Triangles - Special Right Triangle Trigonometry

Trigonometric Functions of Any Angle - Unit Circle, Radians, Degrees, Coterminal & Reference Angles

Finding Exact Values of Trig Functions

How To Evaluate Trigonometric Functions Using Periodic Properties - Trigonometry

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Unit CircleTrigonometrySine FunctionCosine Function45 Degrees60 Degrees30 DegreesReference AnglesQuadrant AnalysisTrig ValuesMath Education