How To Use Reference Angles to Evaluate Trigonometric Functions
TLDRThis educational video script delves into the application of reference angles to determine the values of trigonometric functions. It illustrates the process step by step, starting with finding the sine of 300 degrees using a 30-60-90 triangle and then extending the method to evaluate cosine, tangent, secant, and cosecant at various angles, including negative and pi-based angles. The script emphasizes the importance of understanding special right triangles and the signs of trigonometric functions in different quadrants, providing clear examples to guide learners in solving trigonometric problems.
Takeaways
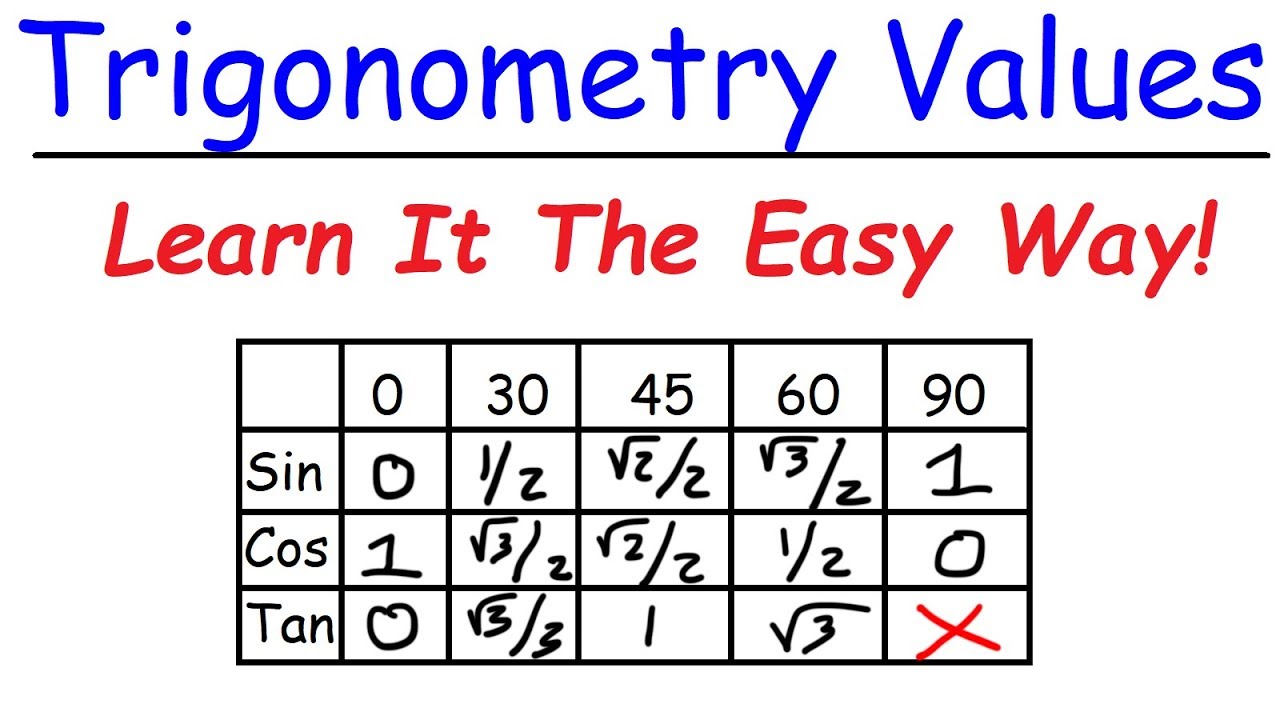
- 📚 The lesson focuses on using reference angles to evaluate trigonometric functions.
- 📐 The sine of 300 degrees is found by converting it to a reference angle of 60 degrees and using a 30-60-90 triangle.
- 📈 The exact value of sine 300 degrees is negative square root of 3 divided by 2, considering the quadrant and the SOHCAHTOA rule.
- 📉 Cosine of 120 degrees is evaluated using the reference angle of 60 degrees and is found to be negative one half.
- 📌 Tangent of seven pi over six is calculated using the reference angle of pi over six and results in square root three divided by three.
- 🔢 The value of sine for negative 135 degrees is determined to be negative square root 2 divided by 2 using a 45-45-90 triangle.
- 📊 To find secant of 330 degrees, cosine of 330 degrees is first calculated, which is positive and results in 2 square root 3 divided by 3 after rationalization.
- 📍 Tangent of 11 pi over four is found to be negative one by considering it as coterminal with three pi over four and using the 45-45-90 triangle.
- 📘 Cosecant of negative four pi over three is calculated by first finding the sine of the coterminal angle, which is two pi over three, resulting in 2 square root 3 divided by 3 after rationalization.
- 📝 The process of evaluating trigonometric functions involves identifying the correct quadrant, reference angle, and using special right triangles to find the values.
Q & A
What is the reference angle for 300 degrees?
-The reference angle for 300 degrees is 60 degrees, which is the difference between 360 degrees and 300 degrees.
How is the sine of 300 degrees calculated using a right triangle?
-The sine of 300 degrees is calculated using a 30-60-90 triangle, with the sine being the opposite side over the hypotenuse, resulting in a negative square root of 3 divided by 2.
In which quadrant is the angle of 120 degrees located?
-The angle of 120 degrees is located in quadrant two.
What is the cosine of 120 degrees in terms of the triangle used?
-The cosine of 120 degrees is negative one half, as it is the adjacent side (which is negative in quadrant two) divided by the hypotenuse.
What is the reference angle for seven pi divided by six radians?
-The reference angle for seven pi divided by six radians is pi over six, which is 30 degrees.
How do you find the tangent of seven pi divided by six radians?
-The tangent of seven pi divided by six radians is found by using the 30-60-90 triangle and calculating the opposite side over the adjacent side, resulting in one over the square root of three, which is then rationalized to square root three divided by three.
What quadrant is negative 135 degrees located in?
-Negative 135 degrees is located in quadrant three.
How is the sine of negative 135 degrees calculated?
-The sine of negative 135 degrees is calculated using a 45-45-90 triangle, with the sine being the opposite side (negative in quadrant three) over the hypotenuse, resulting in negative square root 2 divided by 2 after rationalization.
What is the reference angle for 330 degrees?
-The reference angle for 330 degrees is 30 degrees, found by subtracting 330 from 360.
How do you find the secant of 330 degrees?
-The secant of 330 degrees is found by first determining the cosine of 330 degrees, which is the adjacent side (positive in quadrant four) over the hypotenuse, and then rationalizing it to get 2 square root 3 divided by 3.
What is the relationship between tangent 11 pi divided by four and tangent three pi divided by four?
-Tangent 11 pi divided by four and tangent three pi divided by four are coterminal angles, meaning they have the same terminal side and thus the same tangent value.
How do you determine the cosecant of negative four pi divided by three?
-The cosecant of negative four pi divided by three is found by first determining the sine of the coterminal positive two pi divided by three, which is the opposite side over the hypotenuse, and then taking the reciprocal and rationalizing it to get two square root three over three.
Outlines
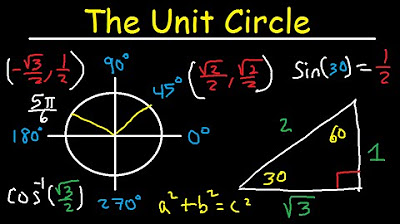
📚 Evaluating Trigonometric Functions Using Reference Angles
This paragraph introduces the concept of using reference angles to evaluate trigonometric functions. It begins by determining the sine of 300 degrees, plotting it in quadrant four, and converting it into a right triangle with a reference angle of 60 degrees. The special 30-60-90 triangle is used to find the sine value, which is the negative square root of 3 divided by 2. The process is then applied to find the cosine of 120 degrees in quadrant two, resulting in a negative value of one half. The tangent of 7π/6 in quadrant three is also calculated, yielding a value of square root of 3 divided by 3. The paragraph concludes with a challenge to find the sine of negative 135 degrees, which is located in quadrant three.
🔍 Advanced Trigonometric Function Evaluations
This section delves into more advanced trigonometric evaluations. It starts with finding the sine of negative 135 degrees, which involves recognizing a 45-45-90 triangle and using it to determine that sine is negative one over the square root of two, rationalized to negative square root of 2 divided by 2. Next, the secant of 330 degrees is calculated by first finding the cosine of 330 degrees in quadrant four, which is positive and results in a value of 2 square root 3 divided by 3 after rationalization. The tangent of 11π/4 is then tackled by recognizing it as coterminal with 3π/4 in quadrant two, leading to a tangent value of negative one. The final example involves finding the cosecant of negative 4π/3, which is coterminal with 2π/3 in quadrant two, and results in a cosecant value of two square root 3 divided by 3 after rationalization.
📐 Understanding Trigonometric Functions with Reference Angles
The final paragraph focuses on reinforcing the understanding of trigonometric functions using reference angles. It revisits the concept of evaluating sine and cosecant with an example of sine for an angle coterminal with 2π/3 in quadrant two. The 30-60-90 triangle is used again to find that sine is the square root of 3 divided by 2. Cosecant, being the reciprocal of sine, is then calculated to be 2 over the square root of 3, which is rationalized to two square root 3 divided by 3. The paragraph emphasizes the positivity of both cosecant and sine in the specified quadrant, highlighting the importance of understanding reference angles and their applications in trigonometry.
Mindmap
Keywords
💡Reference Angles
💡Trigonometric Functions
💡Quadrants
💡Special Right Triangles
💡Sine Function
💡Cosine Function
💡Tangent Function
💡Secant Function
💡Cosecant Function
💡Rationalize
Highlights
Focus on using reference angles to evaluate trigonometric functions.
Exact value of sine of 300 degrees is negative square root of 3 divided by 2.
300 degrees is in quadrant four, close to 270 degrees.
Reference angle for 300 degrees is 60 degrees.
Use of 30-60-90 triangle for trigonometric calculations.
Sine is calculated as opposite over hypotenuse in a right triangle.
Cosine of 120 degrees is negative one half.
120 degrees is located in quadrant two with a reference angle of 60 degrees.
Tangent of seven pi divided by six is square root three divided by three.
Seven pi over six is in quadrant three with a reference angle of 30 degrees.
Tangent is the ratio of opposite side to adjacent side in a right triangle.
Sine of negative 135 degrees is negative square root 2 divided by 2.
Negative 135 degrees is in quadrant three with a reference angle of 45 degrees.
Secant of 330 degrees is 2 square root 3 divided by 3.
330 degrees is in quadrant four with a reference angle of 30 degrees.
Cosine of 330 degrees is positive and calculated as adjacent over hypotenuse.
Tangent of 11 pi divided by four is negative one.
11 pi over four is coterminal with 3 pi over four, located in quadrant two.
Cosecant of negative four pi divided by three is two square root three over three.
Negative four pi over three is coterminal with two pi over three, located in quadrant two.
Cosecant is calculated as the reciprocal of sine.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: