A Simple Trick To Remember Trigonometry Values

The Organic Chemistry Tutor
5 Aug 201811:10
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video offers a simple mnemonic method for remembering trigonometry values using a table format. It covers sine, cosine, and tangent values for key angles: 0, 30, 45, 60, and 90 degrees. The script explains the pattern of these values, introduces the concept of reciprocal trigonometric functions like secant, cosecant, and cotangent, and demonstrates how to use special right triangles (30-60-90 and 45-45-90) along with the 'sohcahtoa' mnemonic to find these values. It also shows how to rationalize fractions involving square roots, providing a comprehensive guide to mastering basic trigonometry.

Takeaways
  • 📊 The video provides a method to remember trigonometry values through a table format.
  • 📈 The sine, cosine, and tangent values for 0, 30, 45, 60, and 90 degrees are explained.
  • 🧩 The sine values increase as the angle increases from 0 to 90 degrees.
  • 🔄 Cosine values are the reverse of sine values, starting at 1 and decreasing to 0.
  • ⏱ Tangent values are calculated as the ratio of sine to cosine for the respective angles.
  • 🚫 Tangent of 90 degrees is undefined because division by zero is not possible.
  • 🔑 The mnemonic 'sohcahtoa' is introduced to help remember the trigonometric ratios.
  • 📐 The 30-60-90 and 45-45-90 right triangles are used to derive trigonometric values.
  • 📝 Rationalization is necessary when dealing with square roots in the denominator.
  • 🔄 Reciprocal trigonometric functions like secant, cosecant, and cotangent are explained.
  • ✅ The video encourages viewers to subscribe and engage with the content for updates.
Q & A

  • What is the purpose of the video?

    -The purpose of the video is to provide a simple way to remember trigonometry values by creating a table and using special reference triangles.

  • What are the angles included in the table created in the video?

    -The angles included in the table are 0 degrees, 30 degrees (pi/6), 45 degrees (pi/4), 60 degrees (pi/3), and 90 degrees (pi/2).

  • What trigonometric functions are covered in the table?

    -The trigonometric functions covered in the table are sine, cosine, and tangent.

  • What is the sine of 0 degrees?

    -The sine of 0 degrees is 0.

  • How is the sine of 30 degrees expressed in the video?

    -The sine of 30 degrees is expressed as one over two or square root one over two.

  • What is the cosine of 90 degrees?

    -The cosine of 90 degrees is 0.

  • How is tangent defined in the video?

    -Tangent is defined as sine divided by cosine in the video.

  • Why is tangent of 90 degrees undefined?

    -Tangent of 90 degrees is undefined because it involves division by zero, as cosine of 90 degrees is 0.

  • What is the special reference triangle used for angles 30, 45, and 60 degrees?

    -The special reference triangle used for angles 30, 45, and 60 degrees is the 30-60-90 triangle and the 45-45-90 triangle.

  • What does SOHCAHTOA stand for in the context of the video?

    -In the video, SOHCAHTOA is a mnemonic used to remember the trigonometric ratios: Sine is Opposite/Hypotenuse, Cosine is Adjacent/Hypotenuse, and Tangent is Opposite/Adjacent.

  • How can you find the secant of 60 degrees using the information from the video?

    -To find the secant of 60 degrees, you take the reciprocal of the cosine of 60 degrees, which is 1 over one half, resulting in a secant of 60 degrees being 2.

  • What is the cotangent of 60 degrees and how do you find it?

    -The cotangent of 60 degrees is the reciprocal of the tangent of 60 degrees. Since tangent of 60 degrees is the square root of 3, the cotangent is 1 divided by the square root of 3, which simplifies to root 3 over 3 after rationalization.

Outlines
00:00
📚 Introduction to Trigonometry Values and Reference Triangles

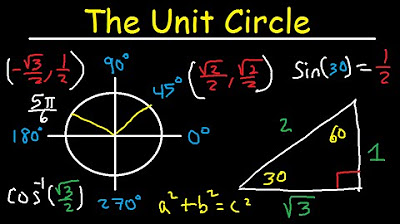
This paragraph introduces a simple method for memorizing trigonometry values by creating a table with sine, cosine, and tangent values for specific angles: 0, 30, 45, 60, and 90 degrees. The values are presented in a pattern that simplifies the sine of 90 degrees to 1, and cosine values are the reverse of sine, moving in the opposite direction. The tangent values are calculated as sine divided by cosine. The paragraph also introduces the concept of using a 30-60-90 triangle and the mnemonic 'sohcahtoa' to evaluate these trigonometric functions, emphasizing the reciprocal relationships between the trigonometric ratios.

05:01
📐 Understanding SOHCAHTOA and Trigonometric Functions

The second paragraph delves deeper into the application of the SOHCAHTOA mnemonic for evaluating trigonometric functions using a 30-60-90 triangle. It explains how to find the sine, cosine, and tangent of 30 and 60 degrees using the opposite, hypotenuse, and adjacent sides of the triangle. The paragraph also demonstrates how to rationalize the tangent of 30 degrees and provides an example of evaluating sine for 60 degrees. Additionally, it introduces the 45-45-90 triangle and shows how to calculate sine, cosine, and tangent of 45 degrees, emphasizing the need to rationalize square roots in fractions.

10:04
🔍 Reciprocal Trigonometric Functions and Rationalizing Techniques

The final paragraph focuses on reciprocal trigonometric functions, such as secant, cosecant, and cotangent, and their evaluation using the values obtained from the reference triangles. It explains that secant is the reciprocal of cosine, and cosecant is the reciprocal of sine, demonstrating the calculation of secant for 60 degrees and cosecant for 60 degrees with rationalization. The paragraph also revisits the concept of cotangent as the reciprocal of tangent and shows how to rationalize the cotangent of 60 degrees. The video concludes with an invitation for viewers to subscribe and engage with the channel for future updates.

Mindmap
Keywords
💡Trigonometry
Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles, particularly right-angled triangles. In the video, trigonometry is the central theme, as the script discusses methods to remember the values of trigonometric functions such as sine, cosine, and tangent for specific angles. The script uses trigonometry to explain how to calculate these values using reference triangles.
💡Sine
Sine is a trigonometric function that relates the ratio of the length of the side opposite an angle to the length of the hypotenuse in a right-angled triangle. In the video, sine values for angles 0, 30, 45, 60, and 90 degrees are discussed, showing how they can be calculated using special right triangles and the mnemonic SOHCAHTOA.
💡Cosine
Cosine is another trigonometric function that represents the ratio of the length of the adjacent side to the hypotenuse in a right-angled triangle. The script explains how cosine values are the reverse of sine values for the angles mentioned, and how they can be derived using the reference triangles and the mnemonic SOHCAHTOA.
💡Tangent
Tangent is a trigonometric function defined as the ratio of the sine of an angle to the cosine of the same angle. The script demonstrates how to calculate tangent values for specific angles by dividing the sine value by the cosine value, and it also shows the reciprocal relationship with the cotangent function.
💡Angle
An angle is a measure of rotation and is a fundamental concept in trigonometry. The script discusses specific angles in degrees (0, 30, 45, 60, and 90 degrees) and how they relate to the values of trigonometric functions within the context of right-angled triangles.
💡Right Triangle
A right triangle is a triangle that has one angle that is exactly 90 degrees. The video script uses two types of right triangles, the 30-60-90 and the 45-45-90 triangles, to demonstrate how to calculate trigonometric function values for specific angles.
💡SOHCAHTOA
SOHCAHTOA is a mnemonic used to remember the trigonometric ratios for sine, cosine, and tangent in relation to the sides of a right triangle. The script explains how each letter of the mnemonic corresponds to a part of the triangle (Sine = Opposite/Hypotenuse, Cosine = Adjacent/Hypotenuse, Tangent = Opposite/Adjacent) and uses it to calculate trigonometric values.
💡Rationalize
Rationalizing a denominator is a mathematical process used to eliminate square roots from the denominator of a fraction. In the script, rationalization is used when calculating trigonometric values to simplify expressions and make them easier to understand and work with.
💡Undefined
In mathematics, a function is said to be undefined when it does not have a value for a given input. In the context of the video, the tangent of 90 degrees is undefined because it involves division by zero, which is not allowed in mathematics.
💡Reciprocal Function
A reciprocal function is a mathematical function that is the multiplicative inverse of another function. The script introduces secant (the reciprocal of cosine), cosecant (the reciprocal of sine), and cotangent (the reciprocal of tangent), showing how they are derived from their respective trigonometric functions.
Highlights

Introduction of a simple method to remember trigonometry values using a table.

Explanation of sine values for 0, 30, 45, 60, and 90 degrees.

Cosine values are the reverse of sine values for the given angles.

Tangent is defined as sine divided by cosine, with examples for each angle.

Tangent of 90 degrees is undefined due to division by zero.

Introduction of the special reference triangle for 30, 45, and 60 degrees.

Explanation of the 30-60-90 triangle and its side lengths.

Use of SOHCAHTOA mnemonic for evaluating trigonometric functions.

Calculation of sine, cosine, and tangent for a 30-degree angle using the 30-60-90 triangle.

Demonstration of evaluating sine of 60 degrees using the reference triangle.

Introduction of the 45-45-90 triangle and its side lengths.

Calculation of sine, cosine, and tangent for a 45-degree angle using the 45-45-90 triangle.

Rationalization of trigonometric ratios involving square roots.

Evaluation of secant of 60 degrees as the reciprocal of cosine 60.

Explanation of cosecant as the reciprocal of sine and its calculation for 60 degrees.

Calculation of cotangent of 60 degrees as the reciprocal of tangent 60.

Encouragement to subscribe to the channel and engage with the content.

Transcripts

Browse More Related Video

How To Find The Exact Values of Trig Functions

Unit Circle Trigonometry - Sin Cos Tan - Radians & Degrees

30-60-90 Triangles - Special Right Triangle Trigonometry

Trigonometry

09 - Unit Circle - Definition & Meaning - Sin(x), Cos(x), Tan(x), - Sine, Cosine & Tangent

Trigonometry Basics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Trigonometry ValuesMnemonicsReference TrianglesEducational ContentMathematicsSine Cosine TangentSOHCAHTOA30-60-90 Triangle45-45-90 TriangleTrigonometry Tutorial