30-60-90 Triangles - Special Right Triangle Trigonometry

The Organic Chemistry Tutor
13 Oct 201703:18
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the properties of a 30-60-90 triangle, a special right triangle with sides in the ratio 1:√3:2. It explains how to calculate trigonometric functions for angles 30 and 60 degrees using this triangle. For a 30-degree angle, sine is 1/2, cosine is √3/2, and tangent is √3/3, while for a 60-degree angle, sine is √3/2, and cosine is 1/2. The script also covers the reciprocal trigonometric functions like cosecant, secant, cotangent, and their respective values for these angles. The goal is to help viewers understand and evaluate common angles without memorizing the entire unit circle, using the 30-60-90 triangle as a reference.

Takeaways
  • 📐 The 30-60-90 triangle is a special right triangle where the sides are in the ratio 1:√3:2.
  • 📏 For a 30-60-90 triangle, the side opposite the 30-degree angle is 1, the side opposite the 60-degree angle is √3, and the hypotenuse is 2.
  • 🧭 Sine of 30 degrees (sin 30) is calculated as the opposite side over the hypotenuse, which is 1/2.
  • 🔄 Cosecant of 30 degrees (csc 30) is the reciprocal of sin 30, resulting in 2.
  • 📐 Cosine of 30 degrees (cos 30) is the adjacent side over the hypotenuse, which simplifies to √3/2.
  • 🔢 Secant of 30 degrees (sec 30) is the reciprocal of cos 30, and after rationalizing, it becomes 2√3/3.
  • 📉 Tangent of 30 degrees (tan 30) is the opposite side over the adjacent side, which rationalizes to √3/3.
  • 🔄 Cotangent of 30 degrees (cot 30) is the reciprocal of tan 30, and it simplifies to √3.
  • 📏 For a 60-degree angle in a 30-60-90 triangle, the opposite side is √3 and the hypotenuse is 2.
  • 📐 Cosine of 60 degrees (cos 60) is the adjacent side over the hypotenuse, which simplifies to 1/2.
  • 📉 Tangent of 60 degrees (tan 60) is the opposite side over the adjacent side, which is √3.
  • 🔄 Cotangent of 60 degrees (cot 60) is the adjacent side over the opposite side, which simplifies to √3/3.
Q & A

  • What is the definition of a 30-60-90 triangle?

    -A 30-60-90 triangle is a special right triangle where the angles are 30 degrees, 60 degrees, and 90 degrees. The sides are in the ratio of 1 : sqrt(3) : 2, with the shortest side being opposite the 30-degree angle, the longest side (hypotenuse) being twice the shortest side, and the side opposite the 60-degree angle being sqrt(3) times the shortest side.

  • What is the length of the side opposite the 30-degree angle in a 30-60-90 triangle?

    -In a 30-60-90 triangle, the side opposite the 30-degree angle is the shortest side and has a length of 1 unit.

  • How long is the hypotenuse of a 30-60-90 triangle?

    -The hypotenuse of a 30-60-90 triangle is twice the length of the shortest side, which means it is 2 units long.

  • What is the sine of a 30-degree angle in a 30-60-90 triangle?

    -The sine of a 30-degree angle is the ratio of the length of the side opposite the angle to the length of the hypotenuse. In a 30-60-90 triangle, sine 30 is 1/2.

  • What is the value of the cosecant of a 30-degree angle?

    -The cosecant is the reciprocal of the sine function. Since sine 30 is 1/2, the cosecant of 30 degrees is 2.

  • How do you calculate the cosine of a 30-degree angle in a 30-60-90 triangle?

    -The cosine of a 30-degree angle is the ratio of the length of the adjacent side to the length of the hypotenuse. In a 30-60-90 triangle, cosine 30 is sqrt(3)/2.

  • What is the secant of a 30-degree angle and how do you rationalize it?

    -The secant of a 30-degree angle is the reciprocal of the cosine, which is 2/sqrt(3). To rationalize it, multiply the numerator and denominator by sqrt(3), resulting in 2sqrt(3)/3.

  • What is the tangent of a 30-degree angle and how is it rationalized?

    -The tangent of a 30-degree angle is the ratio of the opposite side to the adjacent side, which is 1/sqrt(3). When rationalized, it becomes sqrt(3)/3.

  • What is the cotangent of a 30-degree angle?

    -The cotangent is the reciprocal of the tangent function. For a 30-degree angle, cotangent 30 is sqrt(3).

  • How do you find the sine of a 60-degree angle in a 30-60-90 triangle?

    -The sine of a 60-degree angle is the ratio of the length of the side opposite the angle to the length of the hypotenuse. In a 30-60-90 triangle, sine 60 is sqrt(3)/2.

  • What is the value of the cosine of a 60-degree angle in a 30-60-90 triangle?

    -The cosine of a 60-degree angle is the ratio of the length of the adjacent side to the length of the hypotenuse. In a 30-60-90 triangle, cosine 60 is 1/2.

  • How do you calculate the secant of a 60-degree angle?

    -The secant of a 60-degree angle is the reciprocal of the cosine of 60 degrees. Since cosine 60 is 1/2, the secant of 60 degrees is 2.

  • What is the tangent of a 60-degree angle?

    -The tangent of a 60-degree angle is the ratio of the opposite side to the adjacent side, which in a 30-60-90 triangle is sqrt(3).

  • What is the cotangent of a 60-degree angle?

    -The cotangent of a 60-degree angle is the reciprocal of the tangent of 60 degrees, which is 1/sqrt(3) or sqrt(3)/3 when rationalized.

  • How can you use special right triangles to evaluate common angles without memorizing the unit circle?

    -By understanding the properties of special right triangles like the 30-60-90 triangle, you can directly calculate trigonometric ratios for angles of 30, 45, and 60 degrees without needing to memorize the unit circle. This method provides a geometric approach to finding sine, cosine, tangent, and their reciprocals for these specific angles.

Outlines
00:00
📐 Understanding the 30-60-90 Triangle

This paragraph introduces the 30-60-90 triangle, a special right triangle where the sides are in the ratio of 1:√3:2. The speaker explains how to calculate the sine, cosine, tangent, and their reciprocals for angles 30° and 60°. For a 30° angle, sine is 1/2, cosine is √3/2, and tangent is √3/3. For a 60° angle, sine is √3/2, and cosine is 1/2. The reciprocal functions are also calculated, with cosecant of 30° being 2 and of 60° being 2√3/3, secant of 30° being 2√3/3, and of 60° being 2, and cotangent of 60° being √3/3. The paragraph emphasizes the importance of these values for evaluating common angles without memorizing the entire unit circle.

Mindmap
Keywords
💡30-60-90 Triangle
A 30-60-90 triangle is a special right triangle where the angles are 30 degrees, 60 degrees, and 90 degrees. The sides are in the ratio of 1:√3:2, with the shortest side opposite the 30-degree angle being 1 unit, the side opposite the 60-degree angle being √3 units, and the hypotenuse being 2 units. In the video, this triangle is used to derive the values of trigonometric functions for 30 and 60-degree angles, which are essential for understanding the unit circle and evaluating trigonometric functions at common angles.
💡Trigonometric Functions
Trigonometric functions are mathematical functions that relate the angles of a triangle to the lengths of its sides. In the video, sine, cosine, tangent, cosecant, secant, and cotangent are discussed in the context of a 30-60-90 triangle. These functions are fundamental in trigonometry and are used to evaluate angles, particularly in the unit circle and right triangles.
💡Hypotenuse
The hypotenuse is the longest side of a right triangle, which is opposite the right angle. In the context of the 30-60-90 triangle, the hypotenuse is 2 units long. It is used as the reference for calculating the values of trigonometric functions, such as sine and cosine, which are ratios involving the hypotenuse.
💡Sine
Sine is a trigonometric function that represents the ratio of the length of the side opposite an angle to the length of the hypotenuse in a right triangle. In the video, sine of 30 degrees is calculated as 1/2, and sine of 60 degrees is calculated as √3/2, using the properties of the 30-60-90 triangle.
💡Cosecant
Cosecant is the reciprocal of the sine function. It is used to find the angle when the length of the opposite side and the hypotenuse are known. In the script, cosecant of 30 degrees is given as 2, and cosecant of 60 degrees is derived as 2√3/3.
💡Cosine
Cosine is a trigonometric function that represents the ratio of the length of the adjacent side to the hypotenuse in a right triangle. Cosine of 30 degrees is √3/2, and cosine of 60 degrees is 1/2, as demonstrated in the video using the 30-60-90 triangle.
💡Secant
Secant is the reciprocal of the cosine function. It is used to find the angle when the length of the adjacent side and the hypotenuse are known. In the video, secant of 30 degrees is calculated as 2√3/3, and secant of 60 degrees is 2.
💡Tangent
Tangent is a trigonometric function that represents the ratio of the length of the side opposite an angle to the length of the adjacent side in a right triangle. It is also the reciprocal of cotangent. In the video, tangent of 30 degrees is calculated as √3/3, and tangent of 60 degrees is √3.
💡Cotangent
Cotangent is the reciprocal of the tangent function. It is used to find the angle when the lengths of the opposite and adjacent sides are known. In the script, cotangent of 30 degrees is √3, and cotangent of 60 degrees is √3/3.
💡Rationalizing
Rationalizing is the process of eliminating square roots from a fraction by multiplying the numerator and denominator by a form of the conjugate or by another term that will result in a rational number. In the video, rationalizing is used to simplify expressions such as secant of 30 degrees, which is initially 2/√3 and then rationalized to 2√3/3.
💡Unit Circle
The unit circle is a circle with a radius of 1, centered at the origin of a coordinate system. It is used in trigonometry to define trigonometric functions for all angles, not just those in right triangles. In the video, the 30-60-90 triangle is used as a tool to evaluate trigonometric functions at 30 and 60 degrees, which can be applied to the unit circle.
Highlights

Introduction of the 30-60-90 special right triangle with side ratios.

Explanation of the side lengths: 30° opposite is 1, 60° opposite is √3, and the hypotenuse is 2.

Calculation of sine 30° as the ratio of the opposite side to the hypotenuse, resulting in 1/2.

Finding the cosecant of 30° as the reciprocal of sine 30°, which is 2.

Cosine of 30° is the ratio of the adjacent side to the hypotenuse, calculated as √3/2.

Secant of 30° is the reciprocal of cosine 30°, rationalized to 2√3/3.

Tangent of 30° is the ratio of the opposite side to the adjacent side, rationalized to √3/3.

Cotangent of 30° is the reciprocal of tangent 30°, which simplifies to √3.

Starting the evaluation for angles associated with the 60° triangle.

Sine 60° is calculated as the opposite side (√3) over the hypotenuse (2), resulting in √3/2.

Cosecant of 60° is the reciprocal of sine 60°, which is 2√3/3.

Cosine of 60° is the adjacent side (1) over the hypotenuse (2), simplifying to 1/2.

Secant of 60° is the reciprocal of cosine 60°, which is 2.

Tangent of 60° is the opposite side over the adjacent side, simplifying to √3.

Cotangent of 60° is the adjacent side over the opposite side, rationalized to √3/3.

Emphasis on the ability to evaluate common angles like 30, 45, and 60 using special right triangles without memorizing the unit circle.

Transcripts

Browse More Related Video

How To Evaluate Trigonometric Functions Using Periodic Properties - Trigonometry

How To Use Reference Angles to Evaluate Trigonometric Functions

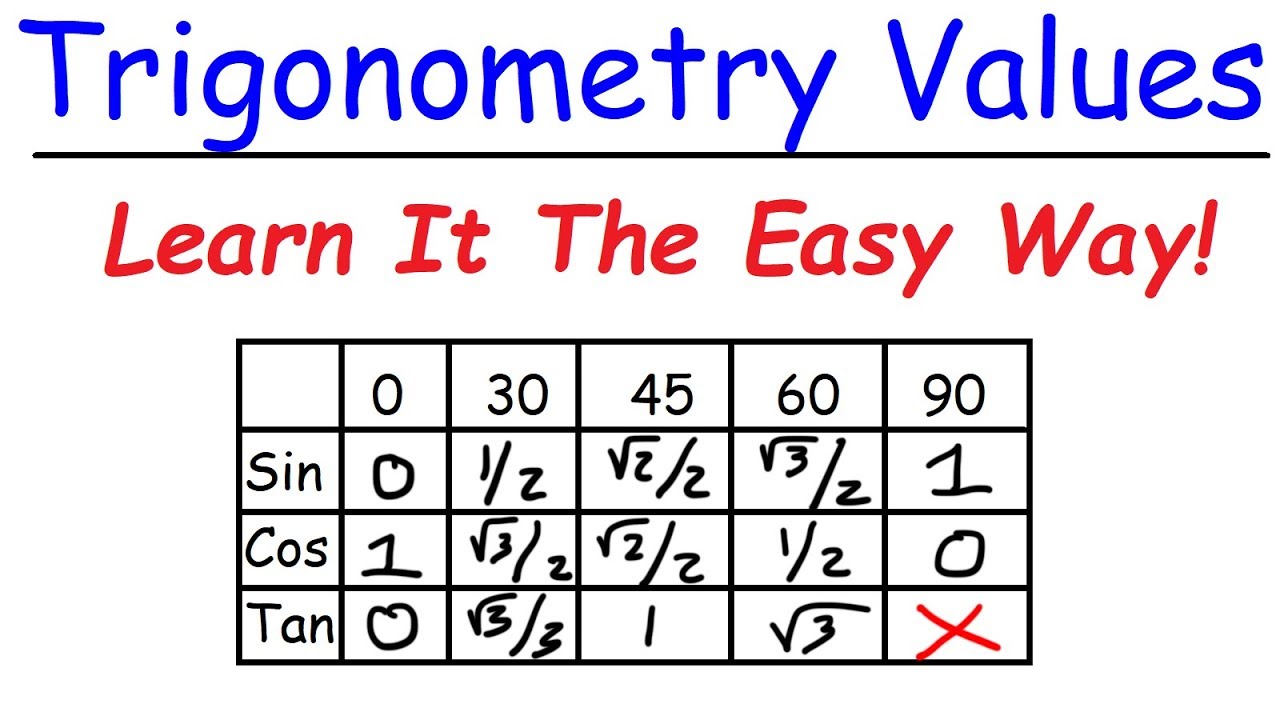
A Simple Trick To Remember Trigonometry Values

Trigonometry - How To Solve Right Triangles

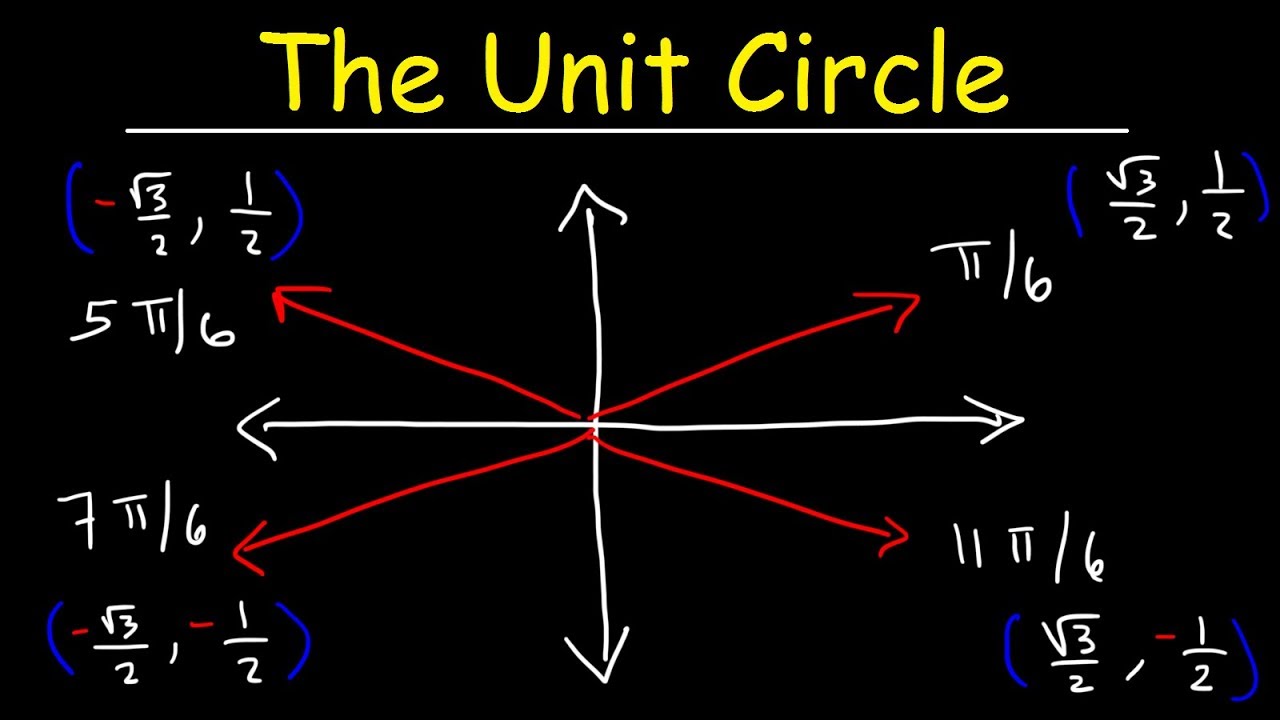
The Unit Circle, Basic Introduction, Trigonometry

Trigonometric Functions: Sine, Cosine, Tangent, Cosecant, Secant, and Cotangent

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Trigonometry30-60-90 TriangleSineCosineTangentCosecantSecantCotangentTrigonometric RatiosMath EducationGeometry