09 - Unit Circle - Definition & Meaning - Sin(x), Cos(x), Tan(x), - Sine, Cosine & Tangent

Math and Science

21 Jul 202052:41

EducationalLearning

32 Likes 10 Comments

TLDRThis lesson delves into the table of trigonometric values for acute angles around the unit circle, emphasizing the importance of understanding sine, cosine, tangent, and their reciprocal functions. The instructor guides students through the process of filling out a table of trig values up to 90 degrees, highlighting the significance of special angles like 30, 45, and 60 degrees. The lesson aims to demystify the unit circle and its applications in trigonometry, using visual aids and the Pythagorean theorem to reinforce the concepts and make the unit circle a familiar and useful tool.

Takeaways

📚 The lesson focuses on understanding the table of trigonometric values for acute angles around the unit circle, emphasizing the importance of familiarity with the unit circle for trigonometry.
🔍 The unit circle is defined as a circle with a radius of one unit, and it is fundamental in understanding trigonometric functions such as sine, cosine, tangent, etc.
📈 The lesson introduces the concept of trigonometric function values at specific angles (30, 45, 60, and 90 degrees) and their relationships on the unit circle.
🌐 The unit circle can be visualized with degree markings and radian markings, but the focus is on degrees for simplicity, especially for acute angles.
🔺 The sine of an angle represents the y-axis projection of a point on the unit circle, while the cosine represents the x-axis projection.
📊 The values of sine and cosine for 30 degrees are 1/2 and √3/2 respectively, and for 45 degrees, both are √2/2.
🔄 The tangent of an angle is calculated as the ratio of sine to cosine, and other trigonometric functions like cotangent, secant, and cosecant can be derived from sine and cosine.
🚫 The lesson discourages rote memorization of the entire table of trigonometric values, instead promoting understanding and the ability to calculate values based on the unit circle.
🔍 The computer demo illustrates the geometric interpretation of sine and cosine values by showing the projections on the x and y axes for different angles on the unit circle.
📈 The lesson emphasizes the symmetry and relationships between angles and their trigonometric values, such as how sine and cosine values are flipped for 30 and 60 degrees.
🔄 The Pythagorean theorem is used to validate the relationships between sine and cosine values, ensuring they satisfy the conditions of a unit circle with a radius of one.

Q & A

What is the primary focus of this lesson?
-The primary focus of this lesson is understanding the table of trigonometric values for acute angles around the unit circle.
Why is the unit circle considered important in trigonometry?
-The unit circle is important in trigonometry because it serves as a fundamental tool for visualizing and calculating sine, cosine, and other trigonometric functions for various angles.
What are the special angles mentioned in the lesson that are critical to understand?
-The special angles mentioned in the lesson are 30 degrees, 45 degrees, 60 degrees, and 90 degrees.
How is the sine of an angle related to the unit circle?
-The sine of an angle is related to the unit circle as it represents the y-coordinate of the point where the angle's terminal side intersects the unit circle.
What is the significance of the Pythagorean theorem in relation to the unit circle?
-The Pythagorean theorem is significant in relation to the unit circle because it ensures that the sine and cosine values, which represent the lengths of the sides of a right triangle, sum up to the hypotenuse (radius) of the unit circle, which is always 1.
What is the tangent of an angle and how is it calculated?
-The tangent of an angle is a trigonometric function that represents the ratio of the sine to the cosine of that angle. It is calculated by dividing the sine value by the cosine value for a given angle.
What are the values of sine and cosine for a 30-degree angle?
-For a 30-degree angle, the sine value is 1/2 and the cosine value is √3/2.
What are the values of sine and cosine for a 45-degree angle?
-For a 45-degree angle, both the sine and cosine values are √2/2.
What are the values of sine and cosine for a 60-degree angle?
-For a 60-degree angle, the sine value is √3/2 and the cosine value is 1/2.
How do the values of sine and cosine change as you move from one quadrant to another in the unit circle?
-As you move from one quadrant to another in the unit circle, the sine and cosine values can change their signs. For example, in the second quadrant, the cosine is negative and the sine is positive; in the third quadrant, both sine and cosine are negative; and in the fourth quadrant, the cosine is positive and the sine is negative.
Why is it beneficial to understand the unit circle and trigonometric functions beyond just memorizing values?
-Understanding the unit circle and trigonometric functions beyond memorization allows for a deeper comprehension of the relationships between angles and their corresponding values, enabling more intuitive problem-solving and a better grasp of trigonometric concepts.

Outlines

00:00

📚 Introduction to Trig Values for Acute Angles

The lesson begins with an introduction to the table of trigonometric values for acute angles around the unit circle. The instructor emphasizes the importance of understanding the unit circle and its role in trigonometry. The plan is to become comfortable with the unit circle and to fill out a comprehensive table of trig values for angles up to 90 degrees, focusing on the sine, cosine, tangent, cotangent, secant, and cosecant of these angles. The instructor aims to demystify the unit circle, which may initially seem complex, and turn it into a useful tool for understanding trigonometry.

05:01

📈 Understanding the Unit Circle and Trig Functions

This paragraph delves into the concept of the unit circle and how it relates to trigonometric functions. The instructor explains how the sine and cosine values are derived from the projections of a point on the unit circle onto the x and y axes, respectively. A computer demo is used to visually demonstrate these concepts, showing how the sine and cosine values change as the angle (θ) increases from 0 to 90 degrees. The paragraph also introduces the idea that the tangent function can be calculated as the ratio of sine to cosine, providing a deeper understanding of the relationship between these fundamental trigonometric functions.

10:03

🔢 Special Angles and Their Trig Values

The instructor focuses on the special angles of 30, 45, and 60 degrees, explaining the trigonometric values for these angles. The sine and cosine values for 30 degrees are given as 1/2 and √3/2, respectively, while for 45 degrees, both are √2/2. The explanation includes a detailed discussion on how these values can be derived from the unit circle and the significance of these special angles in understanding the larger unit circle. The paragraph also touches on the concept of tangent, cotangent, secant, and cosecant for these angles, emphasizing the importance of memorizing these key values for further trigonometric calculations.

15:04

🌀 Filling Out the Trig Table and Memorization Techniques

The lesson continues with the process of filling out the trigonometric table for angles up to 90 degrees. The instructor provides a step-by-step guide on how to calculate the tangent, cotangent, secant, and cosecant values based on the sine and cosine values already discussed. The paragraph emphasizes the importance of understanding the derivation of these values rather than simply memorizing them. The instructor also shares techniques for remembering the special values, such as associating them with the projections on the unit circle and using the Pythagorean theorem to verify the relationships between the values.

20:04

🎯 Mastering Trig Functions and Unit Circle

In the final paragraph, the instructor wraps up the lesson by reiterating the importance of understanding the unit circle and the trigonometric functions associated with it. The focus is on mastering the core concepts and angles, which will enable the learner to tackle more complex trigonometric problems. The instructor encourages the viewer to watch the lesson multiple times to internalize the concepts and to approach the unit circle not as a daunting task but as a fundamental tool for understanding trigonometry. The lesson ends with a preview of future lessons that will cover the unit circle in its entirety, including angles beyond 90 degrees.

Mindmap

Keywords

💡Trigonometry

Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles. It is fundamental to the study of waves, vibrations, and many other physical phenomena. In the video, the讲师 emphasizes the importance of understanding trigonometry, particularly the unit circle and trigonometric functions like sine, cosine, and tangent, which are central to the lesson's theme.

💡Unit Circle

The unit circle is a circle with a radius of 1 unit, centered at the origin of a coordinate plane. It is a fundamental tool in trigonometry for defining the trigonometric functions of an acute angle. In the video, the讲师 explains the unit circle's significance and how it is used to derive trigonometric values, particularly for angles up to 90 degrees.

💡Sine

The sine of an angle in a right triangle is the ratio of the length of the side opposite the angle to the length of the hypotenuse. It is one of the primary functions in trigonometry and is used to describe the y-coordinate of a point on the unit circle. The讲师 emphasizes the importance of memorizing the sine values for special angles like 30, 45, and 60 degrees.

💡Cosine

The cosine of an angle in a right triangle is the ratio of the length of the adjacent side to the length of the hypotenuse. It is another fundamental function in trigonometry, corresponding to the x-coordinate on the unit circle. The讲师 discusses the cosine values for specific angles and their relationship with the unit circle.

💡Tangent

The tangent of an angle is the ratio of the sine to the cosine of that angle. It represents the steepness of the angle and is often used in trigonometric functions to determine the slope of a line. In the video, the讲师 describes how to calculate the tangent using the sine and cosine values.

💡Trig Values

Trig values refer to the values of trigonometric functions, such as sine, cosine, and tangent, for specific angles. These values are crucial for solving problems in trigonometry and understanding the relationships between angles and sides in right triangles. The video focuses on filling out a table of trig values for acute angles around the unit circle.

💡Acute Angles

Acute angles are angles that are less than 90 degrees. In the context of the unit circle, acute angles are used to define points on the circle and their corresponding trigonometric values. The video specifically focuses on acute angles and their trigonometric values.

💡Pythagorean Theorem

The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This theorem is fundamental in trigonometry and is used to relate the sides of a right triangle, which in turn helps in determining trig values.

💡Projection

In the context of the unit circle, projection refers to the length of the segment from the origin to the point on the circle where an angle from the x-axis intersects the circle. The讲师 uses the concept of projection to explain how sine and cosine values are derived from the unit circle, with sine corresponding to the y-axis projection and cosine to the x-axis projection.

💡Trigonometric Functions

Trigonometric functions are mathematical functions that model periodic phenomena, such as the motion of objects in waves or the cycles of tides. The讲师 discusses several of these functions, including sine, cosine, and tangent, and their values for acute angles around the unit circle.

Highlights

The lesson focuses on the table of trigonometric values for acute angles around the unit circle, emphasizing the importance of understanding the unit circle in trigonometry.

The unit circle is a fundamental concept in trigonometry, with a radius of one unit, and it helps to visualize and calculate sine, cosine, and other trigonometric functions.

The lesson aims to demystify the unit circle and make students comfortable with using it as a tool, rather than being intimidated by its complexity.

The table of trig values will be filled out with angles up to 90 degrees, focusing on acute angles, with future lessons covering the full 360 degrees.

The sine, cosine, tangent, cotangent, secant, and cosecant values will be calculated for critical angles such as 30, 45, and 60 degrees.

The lesson includes a computer demo to visually illustrate the concepts of sine and cosine as projections on the x and y axes, respectively.

The tangent function can be calculated as the sine divided by the cosine, which is a key relationship used throughout the lesson.

The sine of 30 degrees is a special value, equal to one-half, while the cosine of 30 degrees is the square root of three divided by two.

At 45 degrees, the sine and cosine values are equal, both being the square root of two divided by two, due to the angle bisecting the right triangle.

For a 60-degree angle, the cosine is one-half, and the sine is the square root of three divided by two, with their values being flipped compared to the 30-degree angle.

The sine of 90 degrees is one, as the projection on the y-axis is the full length of the hypotenuse, while the cosine is zero, with no projection on the x-axis.

The lesson emphasizes the importance of understanding the core fundamental angles and their trigonometric values, rather than memorizing the entire table.

The unit circle's values can be used to find the coordinates of points on its circumference, with the cosine corresponding to the x-coordinate and the sine to the y-coordinate.

The lesson concludes with a reminder that the values for the unit circle are derived from the Pythagorean theorem, explaining the special numbers for 30 and 60-degree angles.

The instructor advises watching the lesson multiple times to fully internalize the concepts and their applications in trigonometry and pre-calculus.

Transcripts

Browse More Related Video

The Unit Circle, Basic Introduction, Trigonometry

Trigonometric Functions of Any Angle - Unit Circle, Radians, Degrees, Coterminal & Reference Angles

Unit Circle Trigonometry - Sin Cos Tan - Radians & Degrees

Trigonometry: Unit Circle

30-60-90 Triangles - Special Right Triangle Trigonometry

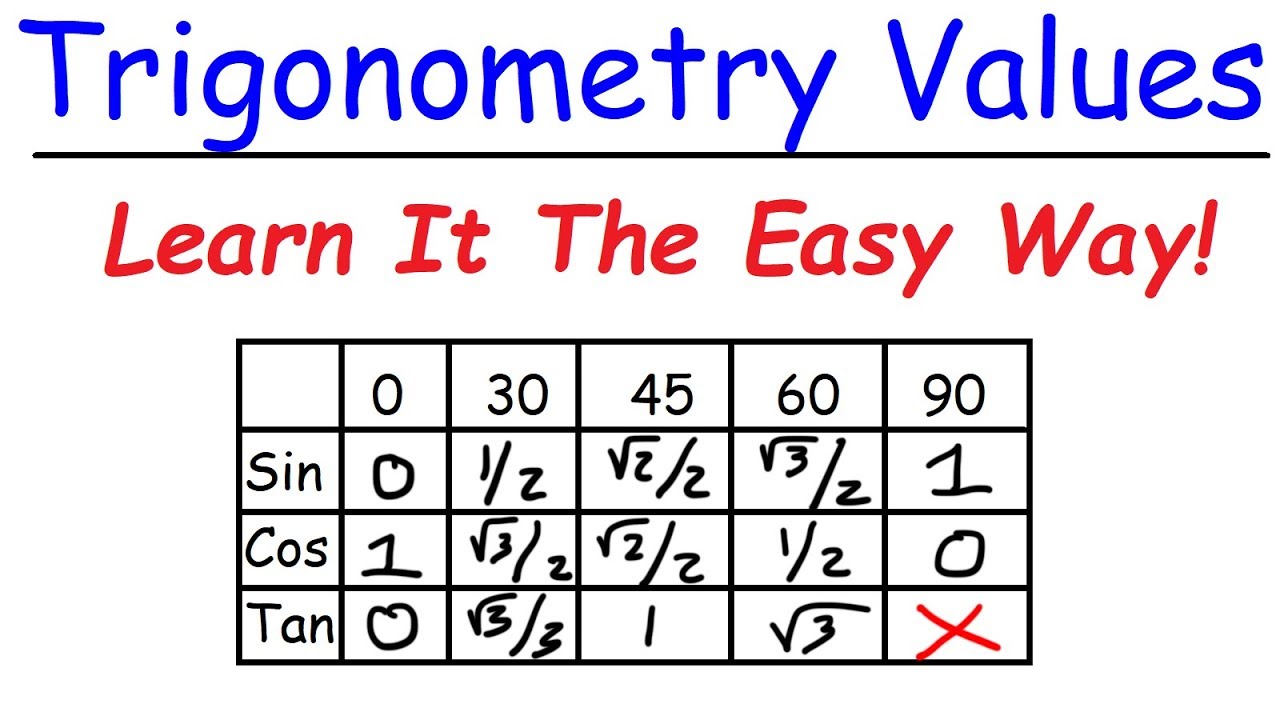
A Simple Trick To Remember Trigonometry Values

Related Tags

Trigonometry Unit Circle Acute Angles Sine Cosine Tangent Trig Values Math Education Pythagorean Theorem Trig Identities Trig Table