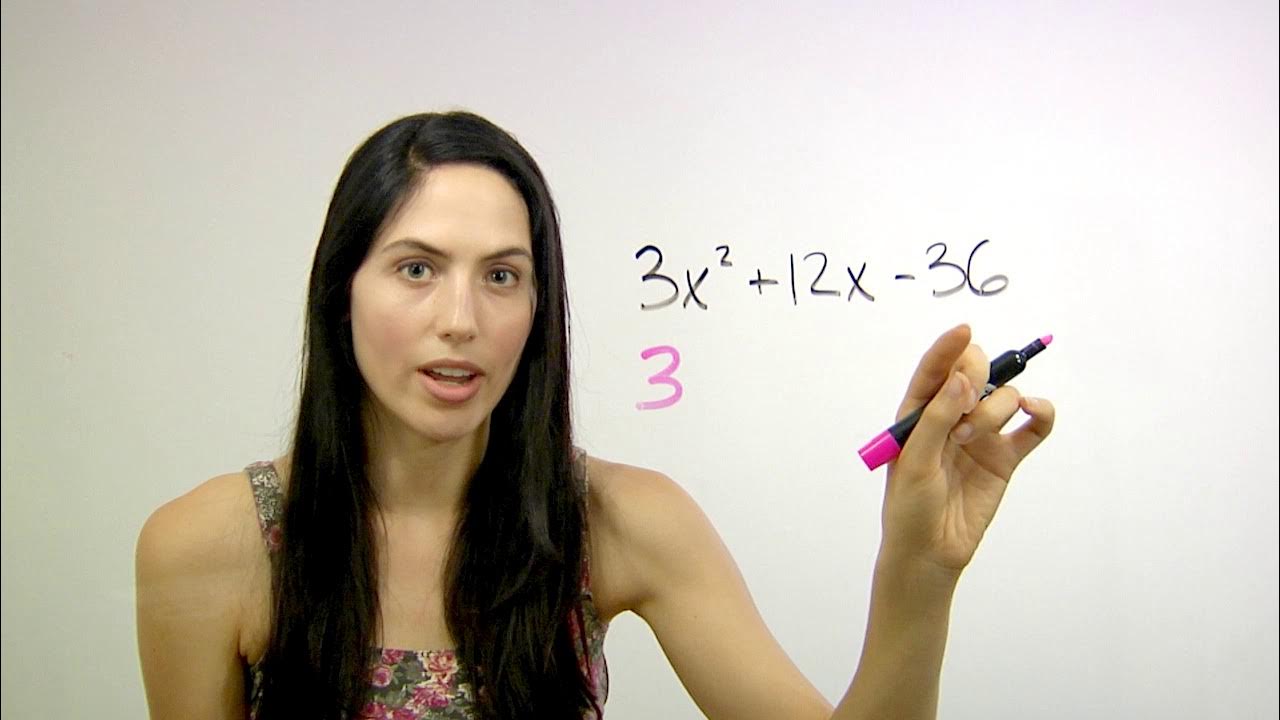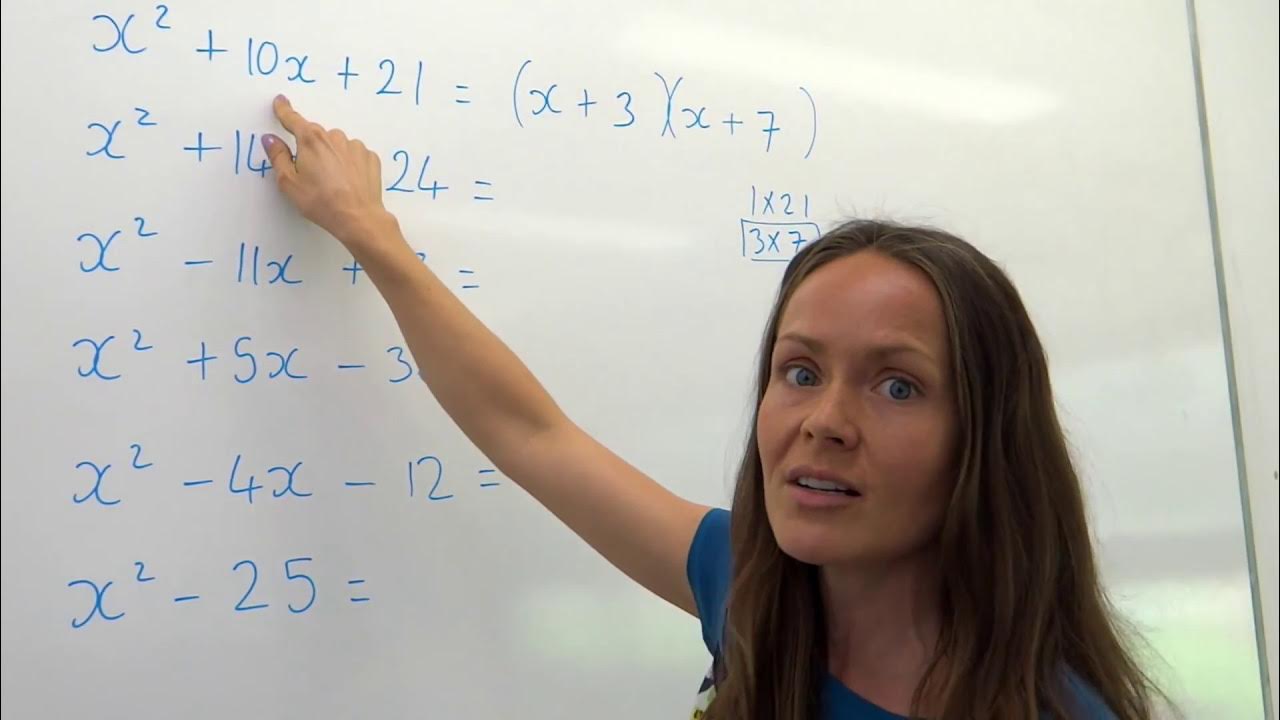Solving Quadratics by Factoring
TLDRThis video teaches techniques for factoring polynomials to solve quadratic equations. It starts by reviewing FOIL method for multiplying binomials, then explains reverse process of factoring trinomials into binomials whose factors multiply to the constant term and add to the linear term. Several examples show how to find correct binomial factors, set them equal to zero, and solve for roots. The technique works for many but not all polynomials. Comprehension questions at the end reinforce key concepts like checking answers, applicability of method, and extending concepts to more complex problems.
Takeaways
- 😀 We can factor polynomials using the reverse FOIL method. Break down the trinomial into binomial factors that multiply to the constant and add to the coefficient of the linear term.
- 😊 To factor a polynomial like x^2 + bx + c, find two numbers that multiply to c and add to b. Put those numbers in the binomial factors.
- 🧐 When factoring polynomials with a negative constant, consider negative and positive factor pairs.
- 🤓 Factoring polynomials allows us to find roots by setting each factor equal to zero.
- 🤔 Be systematic when trying different factor pairs for the constant term until you find the pair that works.
- 😳 Factor binomials starting with x must keep the coefficients straight - don't mix up which term gets multiplied.
- 😉 Always check factored polynomials by multiplying out the binomials using FOIL.
- 😎 Factoring reveals the zeros of a polynomial equation by creating linear factors.
- 🤩 Quadratic equations can be solved by factoring and finding values that make each factor zero.
- 🥳 Factoring polynomials is a useful algebra technique with many applications like solving equations.
Q & A
What is the goal when solving a polynomial equation like AX^2 + BX + C = 0?
-The goal is to find values for X that make the equation true, or in other words, values to plug in for X that make the polynomial expression equal to zero.
How does factoring a polynomial help with solving polynomial equations?
-Factoring allows you to break the polynomial down into binomial factors. If you set the factored polynomial equal to zero, you just need to find values of X that make either binomial factor equal to zero, which will make the whole thing zero.
What does it mean when a term in a polynomial has no coefficient, like the X term?
-When there is no numerical coefficient in front of a term, that means the coefficient is 1 by default. So a term with just X means there is a coefficient of 1 that is not written.
What does FOIL stand for and what does it allow you to do?
-FOIL stands for 'First, Outer, Inner, Last.' It is a process to multiply two binomials together to get a polynomial. FOILing binomials gives you a polynomial expression.
When factoring a polynomial like x^2 + Bx + C, what do you need to find?
-You need to find two numbers, M and N, that can go in the binomial factors, where M and N multiply to give C and add to give B. This allows you to work backwards from the polynomial to extract the original binomials.
Why does order matter when placing factors in binomials during factoring?
-Order matters because one binomial gets multiplied by a coefficient while the other does not. So the factors have to be placed correctly to give the right term when multiplying out the binomials.
What do you do when there is a negative constant term while factoring?
-When there is a negative constant term, you have to consider negative factors in your pairs that multiply to give that term. A product of two negatives is a positive, so negatives are possible.
How do you check an answer after factoring a polynomial?
-After factoring, you can multiply out the binomial factors using FOIL to make sure it gives you the original polynomial expression. You can also plug the solutions back into the original equation to verify the solutions work.
Why does factoring work to solve some polynomials but not others?
-Factoring works whenever you can break a polynomial down into linear binomial factors. But some polynomials have no linear factors, like polynomials with higher order terms. Those cannot be factored into binomials.
What are the key steps to factor a simple polynomial?
-The key steps are: 1) List pairs of factors for the constant term, 2) Find the pair that adds/subtracts to match the x term coefficient, 3) Place the factors correctly into binomials, 4) Check by multiplying binomials back out.
Outlines
🤓 Introduction to Factoring Polynomials
This paragraph introduces factoring polynomials using the reverse FOIL method. It explains that factoring a polynomial allows you to express it as the product of two binomials. This can then be used to find solutions when the polynomial is set equal to zero.
😎 Step-by-Step Examples of Factoring Polynomials
This paragraph provides three step-by-step examples of factoring polynomials using the reverse FOIL method. It shows how to factor trinomials in the form Ax^2 + Bx + C by determining pairs of factors that multiply to C and add to B. Adding or subtracting the factors gives the middle term when FOILed.
Mindmap
Keywords
💡polynomial
💡factor
💡FOIL
💡solve
💡term
💡coefficient
💡trinomial
💡binomial
💡standard form
💡solution
Highlights
The study found a significant increase in life satisfaction for participants after the mindfulness training program.
MRI scans showed changes in brain structure and activity in regions related to awareness, attention and emotion regulation after 8 weeks of mindfulness practice.
Participants practicing mindfulness meditation for 30-40 minutes per day reported lower levels of anxiety, depression and stress.
Mindfulness meditation increased activity in the left prefrontal cortex, a region involved in positive emotions and optimism.
The research provides evidence that mindfulness can lead to cognitive and emotional benefits, and also facilitates structural brain changes.
Mindfulness was shown to reduce mind-wandering and improve working memory and ability to focus attention.
Study found mindfulness training helped obese women lose weight by reducing impulsive eating and binge eating behaviors.
Mindfulness interventions in schools improved academic performance, social skills, classroom behavior and ability to focus among students.
Employees who went through mindfulness training reported lower stress, higher job satisfaction and improved relationships with co-workers.
Mindfulness practice led to decreased aggression, criminal recidivism and substance abuse among prisoner populations.
Mindfulness was an effective intervention for reducing anxiety, depression and pain among patients with chronic health conditions.
Mindfulness meditation reduced loneliness and social isolation among older adults by increasing feelings of social connectedness.
Study found just 10 minutes per day of mindfulness practice produced benefits including reduced stress and improved memory.
Researchers concluded mindfulness-based interventions show promise for treating a variety of psychological and physical health issues.
More high-quality, large-scale randomized controlled trials are needed to further demonstrate the effects of mindfulness training.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: