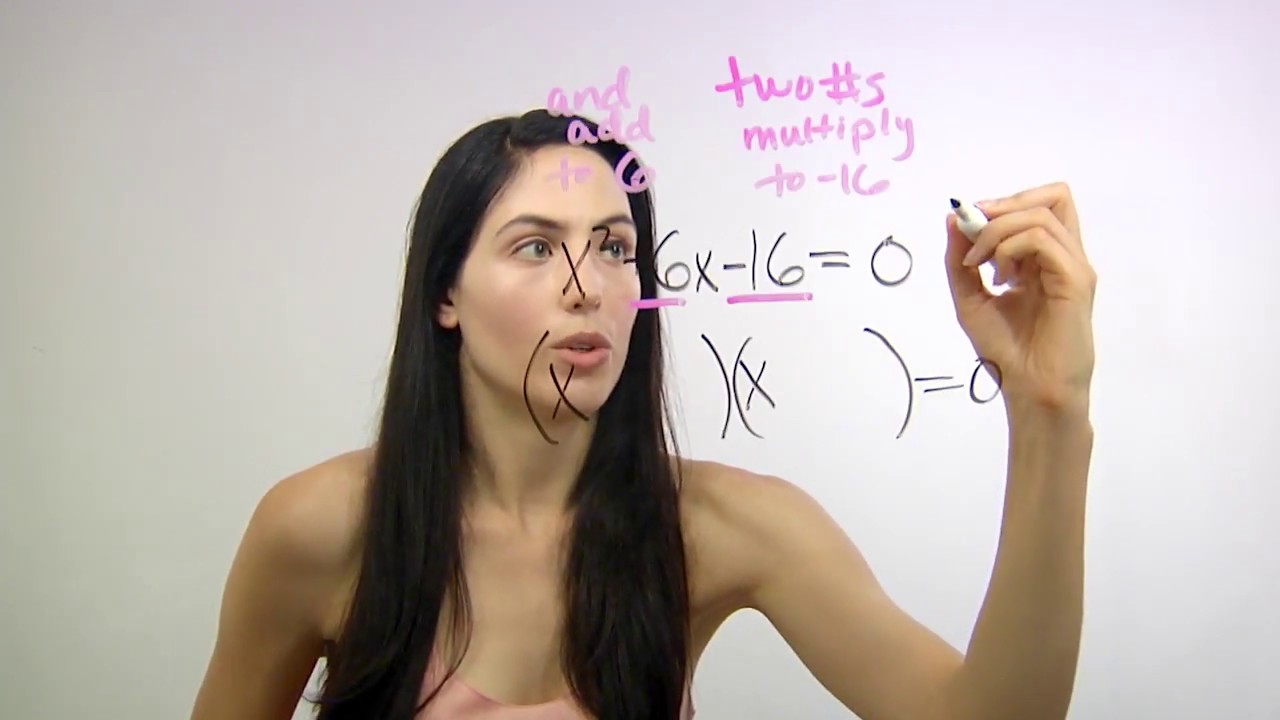Factoring Quadratics... How? (NancyPi)
TLDRIn this educational video, Nancy teaches viewers a methodical approach to factoring quadratic expressions, eliminating the guesswork often associated with the process. She begins with a simple example, showing how to find two numbers that multiply to the constant term and add to the linear coefficient. Nancy then introduces 'The Magic X' technique for more complex cases, demonstrating how to systematically break down and factor expressions, even when they don't start with a squared term. She emphasizes the importance of checking work by multiplying the factors back to the original expression, ensuring accuracy. The video aims to make factoring accessible and enjoyable for all.
Takeaways
- 📚 The video is a tutorial on factoring quadratic expressions, aiming to simplify the process for viewers.
- 🔍 Nancy introduces a methodical approach to factoring that eliminates the need for trial and error.
- 📐 The first step in factoring a quadratic is to find two numbers that multiply to the constant term and add up to the coefficient of the linear term.
- ✅ An example quadratic, \( X^2 + 4X - 12 \), is given to demonstrate the factoring process.
- 🧐 The pairs of numbers that multiply to -12 and add to 4 are listed and evaluated to find the correct pair for factoring.
- 📝 The quadratic is then rewritten as \( (X - 2)(X + 6) \) after identifying the correct pair of numbers.
- 🔄 The process of 'foil and check' is suggested to verify the factoring by multiplying the factors back to the original quadratic.
- 🔑 The 'Magic X' trick is introduced for more complex quadratics that do not start with \( X^2 \), such as \( 3X^2 + 4X - 12 \).
- 🎯 The 'Magic X' involves creating an X structure and finding two numbers that multiply to the product of the first and last terms and add to the middle term.
- 📉 The leading coefficient is used to divide the numbers found in the 'Magic X' method to simplify the factoring process.
- ✍️ The final step is to write the factored form using the simplified numbers, resulting in the correct factorization of the quadratic expression.
Q & A
What is the main topic of Nancy's video?
-The main topic of Nancy's video is teaching how to factor any quadratic expression.
Why might factoring be considered a nightmare for some people?
-Factoring might be considered a nightmare for some people because they feel like they're just doing trial and error without any direction.
What is the first step Nancy suggests to factor a simple quadratic expression?
-The first step Nancy suggests is to find two numbers that multiply to the last number of the quadratic (-12 in the example) and add up to the second number (positive 4).
How does Nancy suggest to find the pairs of numbers that multiply to a specific number?
-Nancy suggests listing all the pairs of numbers that multiply to the specific number in a column and then checking which of these pairs add up to the required number.
What is the 'Magic X' trick mentioned in the video?
-The 'Magic X' trick is a method for factoring tougher quadratic expressions, where you draw an 'X' and use it to find two numbers that multiply to a certain product and add to a certain sum.
How can you check if your factoring is correct?
-You can check if your factoring is correct by multiplying the factors out (using the FOIL method) and verifying that it matches the original quadratic expression.
What should you do if a quadratic expression has a term like 3X squared at the beginning?
-First, check if an overall number can be factored out from the beginning, which simplifies the expression to a standard form that can be factored using the same method as before.
What is the top number of the 'Magic X' used for in the factoring process?
-The top number of the 'Magic X' is the product of the first coefficient and the last constant, which helps in finding the two numbers needed for the factoring process.
How do you use the numbers found in the 'Magic X' method to write the final factorization?
-You divide the numbers found by the leading coefficient and use these fractions to write the final factorization, with the bottom number giving the coefficient of X and the top number giving the constant.
What is the purpose of the 'Magic X' method in factoring quadratic expressions?
-The purpose of the 'Magic X' method is to provide a sure-fire way to factor any quadratic expression, especially when the expression does not start with X squared or has a different leading coefficient.
Outlines
📚 Introduction to Factoring Quadratic Expressions
Nancy introduces the video by explaining that she will teach viewers how to factor any quadratic expression without guesswork. She offers a methodical approach to find two numbers that multiply to the constant term and add up to the linear coefficient. She begins with a simple example, X squared plus 4X minus 12, and guides through the process of identifying the correct pair of numbers that satisfy both conditions. Nancy then demonstrates how to rewrite the quadratic expression as a product of binomials using the identified numbers and suggests verifying the factoring by expanding the binomials.
🔍 Factoring Quadratics with Non-Standard Leading Terms
The second paragraph addresses how to factor quadratics that do not start with X squared, such as 3X squared. Nancy suggests checking for an overall number that can be factored out from all terms, simplifying the expression to a standard form that can be factored using the previously discussed method. She then introduces the 'magic X' trick for more complex cases, illustrating the process with an example where the quadratic starts with 3X squared. The trick involves creating an 'X' structure and finding two numbers that multiply to the product of the leading coefficient and the constant term, and add up to the middle term. These numbers are then divided by the leading coefficient to find the final factors, which are used to rewrite the quadratic expression in factored form. Nancy concludes by emphasizing the importance of checking the factored form against the original expression.
Mindmap
Keywords
💡Factoring
💡Quadratic Expression
💡Magic X
💡Coefficients
💡Product
💡Sum
💡Trial and Error
💡Foiling
💡Constant
💡Binomials
Highlights
Introduction to a method for factoring any quadratic expression without guessing.
Demonstration of factoring a simple quadratic expression: X squared plus 4X - 12.
Explanation of finding two numbers that multiply to the last number and add to the second number in the quadratic.
Listing all pairs of numbers that multiply to -12 and checking which add up to 4.
Identification of the correct pair (-2 and 6) for factoring the given quadratic.
Rewriting the quadratic expression as two sets of parentheses using the identified numbers.
Simplification of the factored expression to X - 2 times X + 6.
Method to check factoring by multiplying out the expression.
Handling quadratics that don't start with X squared by factoring out the common term.
Application of the method to a quadratic with a leading coefficient other than 1.
Introduction of the 'magic X' trick for tougher factoring problems.
Step-by-step guide on using the 'magic X' method for a quadratic starting with 3X squared.
Finding two numbers that multiply to -24 and add to 10 for the 'magic X' method.
Division of the found numbers by the leading coefficient to simplify the factoring.
Writing the final factorization using the simplified fractions.
Verification of the factored expression by multiplying out the terms.
Encouragement to enjoy factoring and a call to action for liking the video.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: