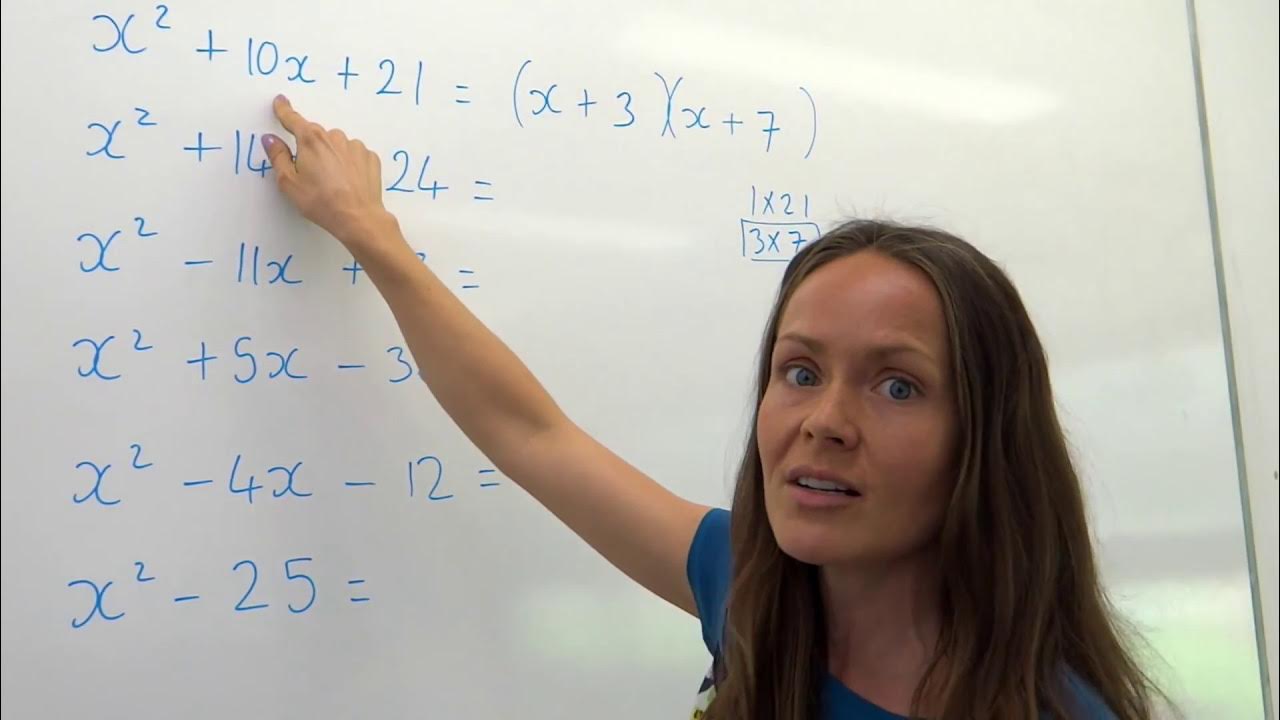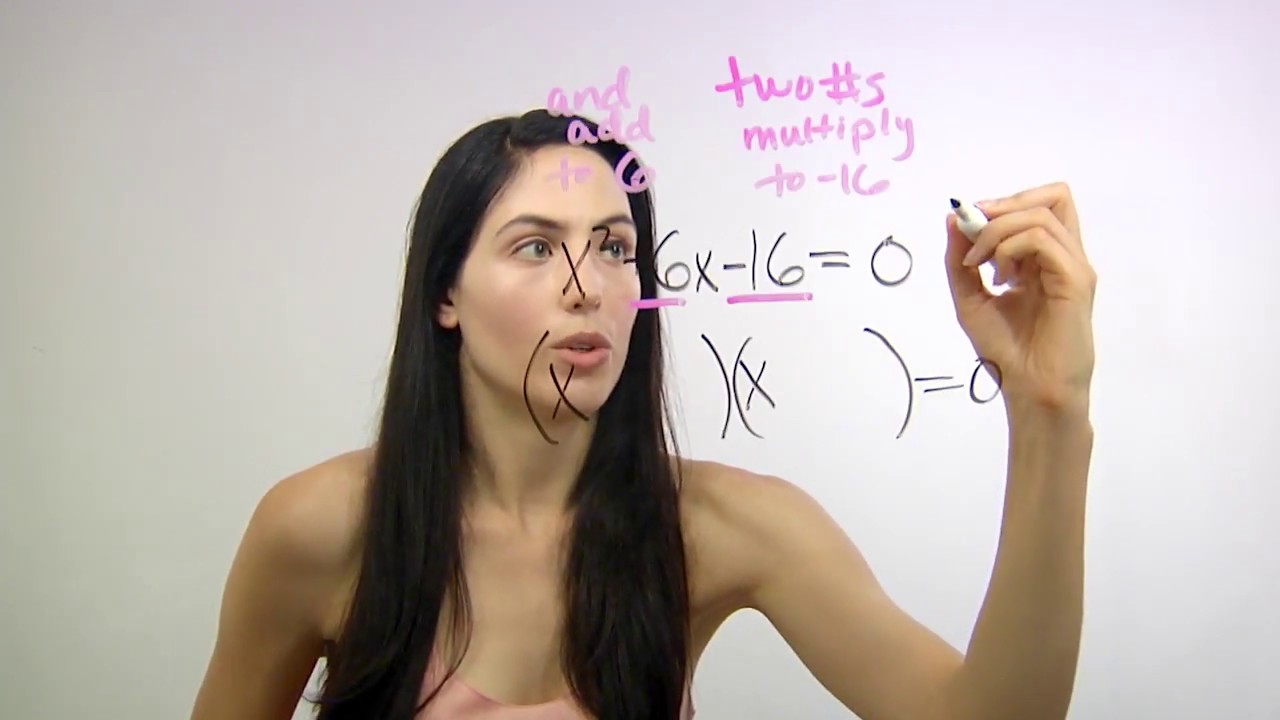Factoring Trinomials - Quick & Simple

The Organic Chemistry Tutor
1 Jul 202019:32
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script offers a comprehensive guide on factoring trinomials, with a focus on finding two numbers that multiply to the constant term and add up to the middle coefficient. It walks through multiple examples, including trinomials with a leading coefficient of one and those that require a different approach due to varying leading coefficients. The script also demonstrates solving quadratic equations using factoring and the zero product property, as well as an advanced technique of reverse factoring using the quadratic formula for more complex cases. The step-by-step explanations aim to make the process clear and accessible for learners.

Takeaways
  • 📘 To factor trinomials with a leading coefficient of 1, find two numbers that multiply to the constant term and add to the middle coefficient.
  • 🔢 Example: For x^2 + 7x + 12, the numbers 3 and 4 multiply to 12 and add to 7, so it factors to (x + 3)(x + 4).
  • 🧮 For trinomials like x^2 + 11x + 30, find pairs of factors of 30 that add to 11, which are 5 and 6, so it factors to (x + 5)(x + 6).
  • 💡 When solving quadratic equations like x^2 - 5x + 6 = 0, factor the trinomial, then use the zero-product property to find the solutions.
  • 📝 For x^2 - 5x + 6 = 0, it factors to (x - 2)(x - 3), giving solutions x = 2 and x = 3.
  • 🔍 For more complex trinomials like x^2 + 3x - 28 = 0, identify pairs that multiply to -28 and add to 3, which are 7 and -4, leading to factors (x + 7)(x - 4).
  • 🔗 To factor trinomials with a leading coefficient other than 1, multiply the leading coefficient by the constant term, then factor normally.
  • 🚀 Example: For 2x^2 - 7x + 6 = 0, factor to (x - 3)(2x - 3) after identifying -3 and -4 as the numbers.
  • 🧠 Using the quadratic formula can help factor more challenging trinomials by finding the roots and reversing the process.
  • ✅ Verification of factoring can be done by multiplying the factors to check if they yield the original trinomial expression.
Q & A

  • What is the primary focus of the video?

    -The video focuses on teaching viewers how to factor trinomials, particularly when the leading coefficient is 1, and also covers solving quadratic equations.

  • What is a trinomial and what is its significance in the video?

    -A trinomial is a polynomial expression with three terms. The video demonstrates methods to factor trinomials, which is crucial for solving quadratic equations.

  • How does the video approach factoring trinomials with a leading coefficient of 1?

    -The video instructs viewers to find two numbers that multiply to the constant term and add up to the middle coefficient, then use these numbers to express the trinomial as a product of two binomials.

  • What is the zero product property mentioned in the video?

    -The zero product property states that if the product of two factors is zero, then at least one of the factors must be zero. This property is used to solve the quadratic equations after factoring the trinomials.

  • Can the method demonstrated in the video be used for all trinomials?

    -The method shown is primarily for trinomials where the leading coefficient is 1. For trinomials with different leading coefficients, additional steps such as factoring by grouping or using the quadratic formula may be necessary.

  • How does the video handle the example of x^2 + 11x + 30?

    -The video factors x^2 + 11x + 30 by finding the numbers 5 and 6, which multiply to 30 and add up to 11, resulting in the factored form (x + 5)(x + 6).

  • What is the purpose of reversing the signs when factoring trinomials with a negative constant term?

    -Reversing the signs helps to find two numbers that multiply to the constant term (positive in this case) and add up to the middle coefficient, which is negative, allowing for the correct factorization.

  • How does the video solve the quadratic equation x^2 - 5x + 6 = 0?

    -The video factors the trinomial to (x - 2)(x - 3) and then uses the zero product property to find the solutions x = 2 and x = 3.

  • What is the quadratic formula, and how is it used in the video?

    -The quadratic formula is used to find the roots of a quadratic equation when factoring is not straightforward. It is given by (-b ± √(b^2 - 4ac)) / (2a). In the video, it is used to solve and factor the trinomial 72x^2 + 17x - 70.

  • Can the quadratic formula be used to factor any trinomial?

    -The quadratic formula can be used to find the roots of any quadratic equation, but it may not always be the most efficient method for factoring trinomials. It is particularly useful when the trinomial does not factor easily with integer coefficients.

  • How does the video demonstrate the process of reverse factoring using the quadratic formula?

    -The video shows how to use the solutions from the quadratic formula to write the original trinomial as a product of binomials, effectively reverse factoring the expression.

Outlines
00:00
🔍 Factoring Trinomials with Leading Coefficient of 1

This paragraph explains how to factor trinomials where the leading coefficient is 1. It details the process of finding two numbers that multiply to the constant term and add to the middle coefficient. Using examples such as x^2 + 7x + 12 and x^2 + 11x + 30, it demonstrates the steps to factor these trinomials into products of binomials.

05:01
🧩 Solving Quadratic Equations by Factoring

This section discusses solving quadratic equations by factoring trinomials. It uses the equation x^2 - 5x + 6 = 0 as an example, showing how to factor the trinomial and then solve for x using the zero product property. The paragraph also covers another example, x^2 + 3x - 28 = 0, illustrating the factoring process and verification of solutions by plugging them back into the original equation.

10:02
🔢 Factoring Trinomials with Leading Coefficient Greater than 1

This paragraph addresses factoring trinomials where the leading coefficient is not 1, using the example 2x^2 - 7x + 6 = 0. It explains the steps of multiplying the leading coefficient by the constant term, finding suitable factors, and using grouping to factor the trinomial. The process is demonstrated in detail, including how to verify the factored form by multiplying the binomials.

15:05
🧮 Using the Quadratic Formula for Complex Trinomials

The final section explores factoring more challenging trinomials, such as 72x^2 + 17x - 70, using the quadratic formula. It explains the step-by-step process of applying the quadratic formula, simplifying the results, and reverse factoring to find the binomial factors. The paragraph concludes by verifying the factorization through multiplication and ensuring the result matches the original trinomial.

Mindmap
Keywords
💡Factoring Trinomials
Factoring trinomials refers to the mathematical process of breaking down a trinomial, which is a polynomial with three terms, into a product of binomials. This concept is central to the video's theme as it demonstrates various methods to factor trinomials with leading coefficients equal to and not equal to one. For instance, the script shows how to factor a trinomial where the leading coefficient is 1 by finding two numbers that multiply to the constant term and add up to the middle coefficient.
💡Leading Coefficient
The leading coefficient is the numerical factor that stands before the variable raised to its highest power in a polynomial. In the context of the video, the leading coefficient plays a crucial role in determining the method used for factoring trinomials. The script discusses scenarios where the leading coefficient is 1, as well as cases where it is not 1, each requiring a different approach to factorization.
💡Constant Term
The constant term is the term in a polynomial that does not contain any variables. It is a key element in the factoring process, as the script explains the need to find two numbers that multiply to the constant term when factoring trinomials. For example, when factoring a trinomial with a constant term of 12, the script shows how to find numbers that multiply to 12 and add to the middle coefficient.
💡Middle Coefficient
The middle coefficient is the numerical factor associated with the second-highest power of the variable in a trinomial. The video script emphasizes the importance of this term in the factoring process, as it must add with another number (which multiplies to the constant term) to equal the middle coefficient of the original trinomial. This is exemplified when the script solves for trinomials and finds pairs of numbers that add up to the middle coefficient.
💡Zero Product Property
The zero product property states that if the product of two factors is zero, then at least one of the factors must be zero. In the video, this property is used to solve quadratic equations after factoring the trinomials. For example, once a trinomial is factored into binomials set equal to zero, the property allows solving for the variable by setting each binomial equal to zero and solving for x.
💡Quadratic Equation
A quadratic equation is a polynomial equation of degree two with one variable. The video script discusses how to solve these equations by factoring the quadratic expressions into binomials and then applying the zero product property. The script provides examples of quadratic equations and demonstrates the step-by-step process of factoring and solving for the variable x.
💡Greatest Common Factor (GCF)
The greatest common factor, or GCF, is the largest number that divides two or more numbers without leaving a remainder. In the context of the video, the GCF is used in the process of factoring by grouping, where the GCF is factored out from each group of terms in a trinomial with a leading coefficient not equal to one. The script illustrates this by showing how to factor a trinomial by taking out the GCF from terms and then factoring further.
💡Factor by Grouping
Factor by grouping is a technique used to factor polynomials, especially when the leading coefficient is not one. The video script explains this method by showing how to rearrange and group terms in a trinomial so that a common factor can be factored out from each group. This approach simplifies the expression into a product of binomials, as demonstrated with examples in the script.
💡Quadratic Formula
The quadratic formula is a method used to solve quadratic equations when factoring is not straightforward. It is given by the formula: x = (-b ± √(b² - 4ac)) / (2a), where a, b, and c are coefficients from the quadratic equation ax² + bx + c = 0. The video script introduces the quadratic formula as an alternative method to find the factors of a trinomial when direct factoring is complex or inefficient.
💡Reverse Factoring
Reverse factoring, as discussed in the video, involves using the solutions obtained from the quadratic formula to express the original trinomial as a product of binomials. This technique is particularly useful for trinomials that are difficult to factor directly. The script demonstrates how to use the solutions from the quadratic formula to rewrite the trinomial in factored form, thereby simplifying the expression.
Highlights

Introduction to factoring trinomials with a leading coefficient of 1.

Explanation of finding two numbers that multiply to the constant term and add to the middle coefficient.

Example: Factoring x^2 + 7x + 12 by identifying the factors of 12.

Detailing the process of factoring x^2 + 7x + 12 into (x + 3)(x + 4).

Example: Factoring x^2 + 11x + 30 by identifying the factors of 30.

Detailing the process of factoring x^2 + 11x + 30 into (x + 5)(x + 6).

Example: Solving the quadratic equation x^2 - 5x + 6 = 0 by factoring.

Explanation of the zero product property to find solutions x = 2 and x = 3.

Example: Factoring and solving x^2 + 3x - 28 = 0 by identifying factors of -28.

Detailing the process of factoring x^2 + 3x - 28 into (x + 7)(x - 4) and finding solutions x = -7 and x = 4.

Introduction to factoring trinomials with a leading coefficient not equal to 1.

Example: Factoring 2x^2 - 7x + 6 by multiplying the leading coefficient by the constant term.

Explanation of replacing the middle term and factoring by grouping for 2x^2 - 7x + 6.

Example: Factoring and solving 72x^2 + 17x - 70 using the quadratic formula.

Explanation of using the quadratic formula to find the solutions and reverse factoring the trinomial.

Transcripts

Browse More Related Video

Box Method of Factoring Trinomials (10 Examples)

The Maths Prof: Factorising Quadratics (putting into double brackets)

Factoring Trinomials

Factoring Quadratic Expressions Pt. 1

Using Factoring to Solve Quadratics (Precalculus - College Algebra 18)

How to Solve Quadratic Equations by Factoring (NancyPi)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
FactoringTrinomialsQuadraticEquationsMathematicsEducationalTutorialSolvingAlgebraFormulas