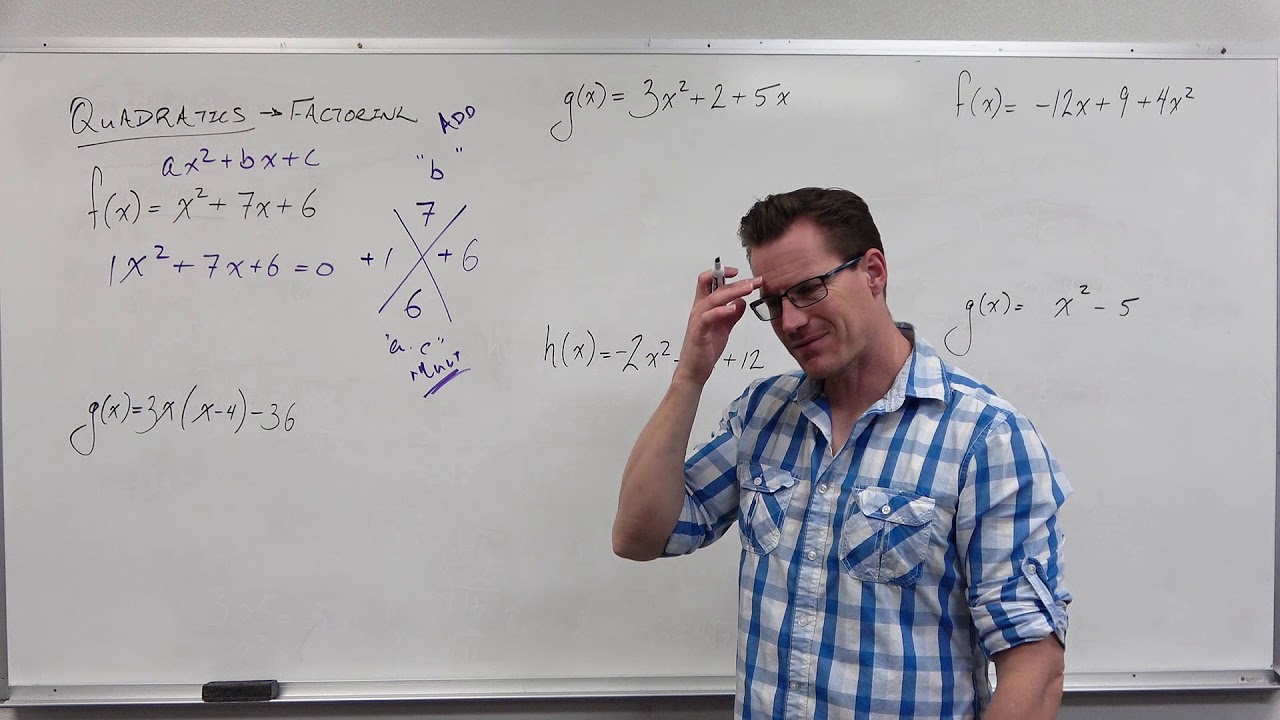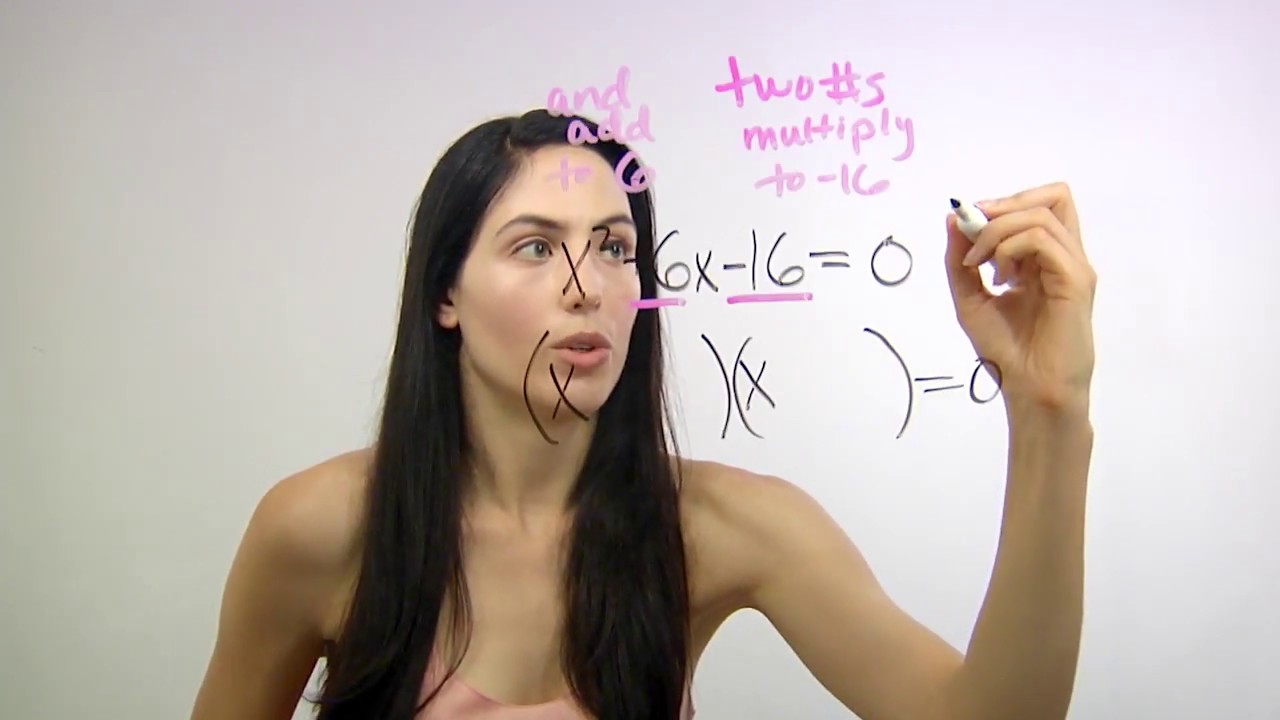The Maths Prof: Factorising Quadratics (putting into double brackets)
TLDRThis educational video script offers a step-by-step guide on factoring quadratics using double brackets. It emphasizes the importance of knowing multiplication tables for efficiency and demonstrates how to find pairs of factors that multiply to the constant term and add up to the coefficient of the linear term. The script covers various examples, including those with negative factors and no linear term, providing a clear method for correctly setting up and solving quadratic equations.
Takeaways
- 📚 The video is a tutorial on factoring quadratics, focusing on the use of double brackets to simplify expressions.
- 🔍 The first step in factoring is to identify the correct pair of numbers that multiply to the constant term and add up to the coefficient of the linear term.
- 🧩 The importance of knowing times tables is emphasized for quick and efficient problem-solving.
- 🔢 The script demonstrates how to find factors of numbers like 21, 24, 18, and 36, and how to use them in the context of quadratic expressions.
- ➕ The process involves choosing pairs of factors that not only multiply to the constant term but also add to the coefficient of the middle term.
- ⚠️ The order of the numbers inside the brackets does not affect the outcome, but the signs do, especially in expressions with a minus sign.
- 🔄 The script uses the method of checking by multiplying out the factors to ensure the original expression is correctly represented.
- 📉 In cases with a negative constant term, both factors must be negative to result in a positive product, and they must add to a negative sum.
- 📈 The tutorial also covers scenarios where there is no x term, indicating the need for careful selection of factors that multiply to a negative constant and add to zero.
- 📝 The video concludes with a teaser for the next topic, which is the difference of two squares, another factorization technique.
- 🎓 The overall message is that practice and understanding of the underlying principles are key to mastering the factorization of quadratics.
Q & A
What is the main topic of the video?
-The main topic of the video is teaching viewers how to factor quadratic expressions.
What is a double bracket in the context of the video?
-In the context of the video, a double bracket refers to a pair of parentheses used in algebraic expressions, specifically when factoring quadratics.
Why is it important to know multiplication tables when factoring quadratics?
-Knowing multiplication tables is important for quickly identifying factors that multiply to give the constant term in a quadratic expression.
What is the first step in factoring a quadratic expression according to the video?
-The first step is to identify the coefficient of the squared term and write it as a product with the variable, which gives the squared term.
Why are the factors in the double brackets both plus in the first example?
-The factors are both plus because the middle term of the quadratic expression is positive, indicating that the factors must multiply to give a positive constant term and add up to the coefficient of the linear term.
What is the process for finding the correct pair of factors in the double brackets?
-The process involves identifying all possible pairs of factors for the constant term, and then selecting the pair that also adds up to the coefficient of the linear term.
What is the significance of the order of factors in the double brackets?
-The order of factors in the double brackets does not matter as long as the correct factors are chosen to satisfy both the multiplication and addition conditions.
How does the presence of a negative sign affect the factoring process in the third example?
-In the third example, the presence of a negative sign means that both factors must be negative to result in a positive product, and they must add up to a negative sum to match the linear term coefficient.
What is the strategy for dealing with a negative constant term in the fourth example?
-For a negative constant term, the strategy involves finding pairs of negative factors that multiply to give the negative constant and add up to the negative sum of the linear term coefficient.
What is the purpose of checking the factored expression by multiplying it out?
-Checking the factored expression by multiplying it out serves as a verification step to ensure that the factoring process has been done correctly and that it reverts back to the original quadratic expression.
What is the next topic the video hints at covering after the current one on factoring quadratics?
-The next topic hinted at is the difference of two squares, which is another factoring technique.
Outlines
📚 Factoring Quadratics with Double Brackets
The first paragraph introduces the concept of factoring quadratics using double brackets. The mascot demonstrates how to factor the first quadratic expression, x^2 + 10x + 21, by identifying the correct pair of factors for 21 that add up to 10. The process involves multiplying x by x to get x^2, then finding the factors (3 and 7), and placing them in the brackets to form the correct factorization. The mascot emphasizes the importance of checking the factorization by multiplying it out to ensure it matches the original expression. This method is applied to a second example, x^2 + 14x + 24, where the factors of 24 that add up to 14 are identified as 2 and 12.
🔍 Factoring Quadratics with Negative Coefficients
The second paragraph continues the theme of factoring quadratics but introduces negative coefficients. The mascot explains how to factor expressions with negative constants by using negative factors that multiply to the constant and add up to the coefficient of the x term. For example, the expression x^2 - 11x + 18 is factored by finding the negative factors of 18 that add up to -11, which are -2 and -9. The mascot also discusses the importance of knowing times tables for quick factor identification and emphasizes the need to check the factorization by multiplying it out. The process is further illustrated with additional examples, including one where there is no x term, indicating a difference of squares factorization.
Mindmap
Keywords
💡Factoring
💡Quadratics
💡Double Brackets
💡Factors
💡Multiplying Out
💡Coefficients
💡Positive and Negative
💡Times Tables
💡Difference of Two Squares
💡Checking
Highlights
Introduction to factoring quadratics using double brackets method.
Explanation of how to obtain x squared by multiplying x by x.
Importance of choosing factors that both multiply to give the constant term and add up to the coefficient of the linear term.
Example of finding factors of 21 that add up to 10 for the quadratic equation x^2 + 10x + 21.
Demonstration of checking the factorization by multiplying out the brackets.
Moving on to the second example with a different set of numbers to factorize.
Emphasis on knowing times tables for efficiency in factorization.
Process of finding factors of 24 that add up to 14 for the quadratic equation x^2 + 14x + 24.
Introduction of a negative constant term and its impact on the selection of factors.
Example of factoring a quadratic with a negative constant term, focusing on negative factors that add up to a negative number.
Highlighting the importance of order and sign when placing factors in the brackets.
Approach to factoring when there is no x term, indicating a plus zero in the quadratic equation.
Explanation of how to handle negative factors for the quadratic equation x^2 - 11x + 18.
Teaching the method of writing down all possible factors to easily spot the correct pair.
Transition to the next video topic, the difference of two squares, as another factorization technique.
Conclusion and summary of the key points covered in the video.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: