Video 57 - Embedded Manifolds
TLDRThis video script introduces the concept of extending tensor calculus from Euclidean spaces to non-Euclidean manifolds. It defines embedded manifolds, or sub-manifolds, which are subsets of larger manifolds known as ambient spaces. The script uses the plane and the sphere as examples to illustrate the concept of manifolds and their properties, including co-dimension. It also discusses the need for expanding tensor calculus to handle non-Euclidean spaces, as traditional Euclidean-based analysis is insufficient. The video aims to deepen the understanding of manifolds and their role in advanced mathematical analysis.
Takeaways
- 📚 The script discusses the extension of tensor calculus from Euclidean spaces to non-Euclidean manifolds, emphasizing the importance of this step for a deeper understanding of the subject.
- 🌐 It introduces the concept of an embedded manifold, or sub-manifold, as an m-dimensional manifold that is a subset of a larger, in-dimensional manifold known as the ambient space.
- 🔢 The co-dimension is defined as the difference in dimensionality between the manifold and the sub-manifold, with the simplest example being a plane, which is a 2D sub-manifold in a 3D space.
- 📏 The script explains the process of setting up a coordinate system on a plane, using u and v as coordinates to locate points, which is a review of concepts from an earlier video.
- 📈 The video uses the example of a sphere to illustrate a non-Euclidean sub-manifold, where points are identified by theta and phi values, and the surface is embedded in a 3D Euclidean space.
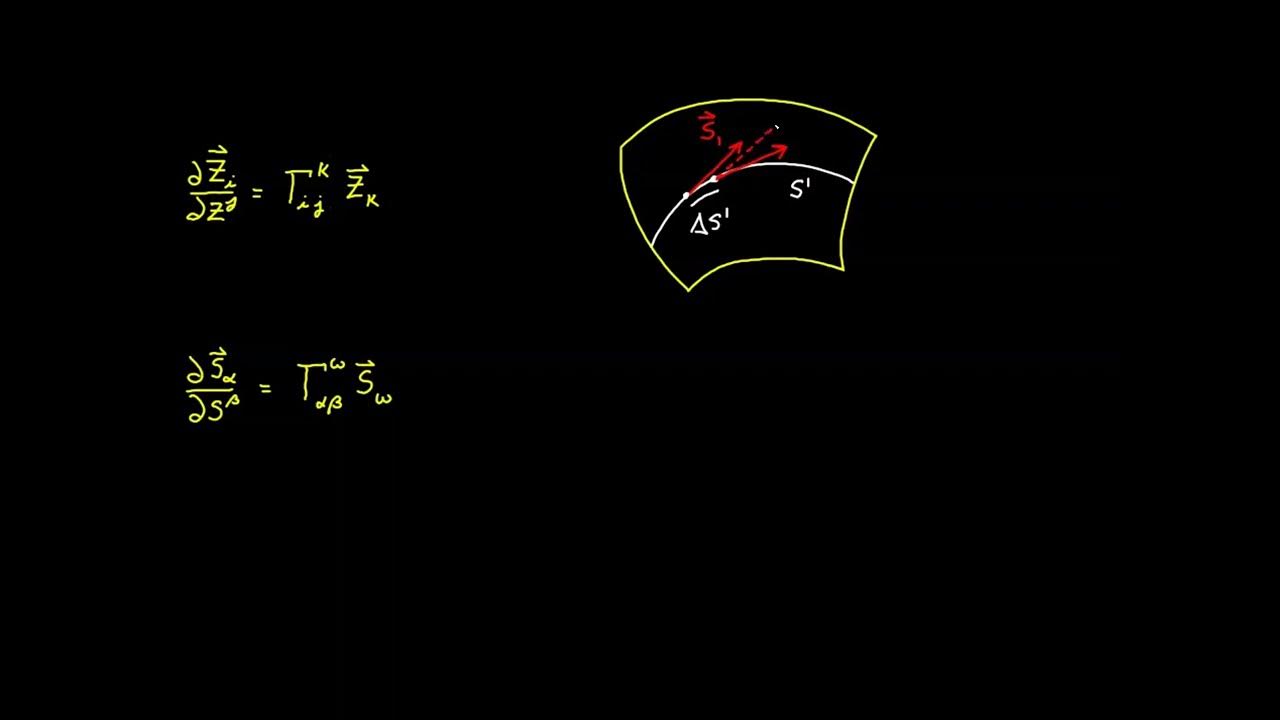
- 📊 The concept of a manifold is further explored with the example of a spiral, which is a 1D sub-manifold in a 3D space, demonstrating how the degrees of freedom can be reduced from three to one.
- 🌀 The script differentiates between a manifold and a space, stating that a manifold is a space that locally resembles Euclidean space and is characterized by being smooth, continuous, and differentiable.
- 📉 The importance of the tangent plane is highlighted, showing how it can be used to create a local Euclidean coordinate system near any point on the manifold.
- 🌍 The Earth is used as an example to explain how large-scale spaces can appear flat at a local level due to their immense size compared to human-scale neighborhoods.
- 📐 The script provides a mathematical approach to quantify the deviation of a curved surface from a straight line, using the Pythagorean theorem and an infinite series approximation for small values.
- 🏙️ Real-world examples, such as the Lake Pontchartrain Bridge and the Brooklyn Bridge, are used to demonstrate the practical application of the mathematical concepts discussed in the script.
Q & A
What is the significance of mastering tensor calculus for Euclidean spaces?
-Mastering tensor calculus for Euclidean spaces provides a foundational understanding of how tensor operations work in flat, geometric spaces, which is a crucial milestone before extending the analysis to more complex, non-Euclidean manifolds.
What are non-Euclidean manifolds in the context of tensor calculus?
-Non-Euclidean manifolds are spaces that do not adhere to the properties of Euclidean geometry, such as the surface of a sphere, where straight lines cannot be drawn, and the space is curved or has a different metric structure.
What is an embedded manifold or sub-manifold?
-An embedded manifold, or sub-manifold, is an m-dimensional manifold that is a subset of a larger, more inclusive n-dimensional manifold, known as the ambient space. The difference in dimensionality between the two is called the co-dimension.
How is a plane an example of an embedded manifold?
-A plane is an example of an embedded manifold because it is a two-dimensional surface that lies within a three-dimensional space (the ambient space). It has a co-dimension of one, as it is a subset of the larger space with reduced degrees of freedom.
What is the difference between a Euclidean space and a non-Euclidean space?
-A Euclidean space is a space that follows the principles of Euclidean geometry, where straight lines can be drawn and the Pythagorean theorem applies. A non-Euclidean space, on the other hand, has a different geometric structure where these principles do not hold, such as on the surface of a sphere.
Why is the surface of a sphere considered a non-Euclidean sub-manifold?
-The surface of a sphere is considered a non-Euclidean sub-manifold because it cannot have straight lines (geodesics are great circles instead), and thus it does not allow for an affine coordinate system like a Euclidean space does.
What is the concept of a manifold in mathematics?
-A manifold in mathematics is a topological space that locally resembles Euclidean space near each point. It is a space that is smooth, continuous, and differentiable, allowing for the application of calculus and other mathematical tools.
What does it mean for a space to be 'locally flat'?
-A space is considered 'locally flat' if, when examining a sufficiently small neighborhood around any point, the space appears to be indistinguishable from a flat, Euclidean space. This property is fundamental to the definition of a manifold.
How can the concept of a manifold be applied to the Earth's surface?
-The Earth's surface can be considered a manifold because, despite being round, it appears flat on a small scale due to its large size. This allows for the application of Euclidean geometry in everyday life, such as in mapping and navigation.
What is the significance of the tangent plane in the context of manifolds?
-The tangent plane at a point on a manifold provides a local linear approximation of the manifold's surface. It is used to define a local coordinate system where the manifold appears flat, facilitating the application of calculus and other mathematical techniques.
How does the script illustrate the concept of 'local flatness' with an elliptic paraboloid?
-The script uses an elliptic paraboloid to demonstrate that as one zooms in on a point, the surface appears to flatten out, making the difference between the surface and a tangent plane indistinguishable. This illustrates the local flatness property of manifolds.
What is the practical application of understanding the deviation from a straight line on a curved surface like a bridge?
-Understanding the deviation from a straight line on a curved surface is important in engineering and construction, where precision in design is necessary to account for the curvature of the Earth or other factors, ensuring structural integrity and accuracy.
Outlines
📚 Introduction to Non-Euclidean Manifolds
This paragraph introduces the concept of extending tensor calculus to non-Euclidean manifolds, following the mastery of Euclidean spaces. The author emphasizes the brilliance of tensor calculus in this context and begins with embedded manifolds, specifically sub-manifolds, which are subsets of a higher-dimensional 'ambient space'. The co-dimension is the difference in dimensionality between the two. The simplest example given is a plane, which is a 2D manifold in a 3D space, with coordinates u and v for the plane and x, y, z for the ambient space. The paragraph explains the arbitrary nature of choosing an origin and axis orientation and how a plane is a subset of a 3D space, illustrating the concept of a sub-manifold.
🌐 Exploring Embedded Manifolds: Planes and Spheres
The second paragraph delves deeper into embedded manifolds, contrasting the Cartesian coordinate systems applicable to both the ambient space and the sub-manifold, which are Euclidean spaces. It uses the example of a plane and then moves on to a sphere, highlighting the difference between them. While both are 2D manifolds in a 3D space, the sphere's surface is a non-Euclidean sub-manifold because it cannot have straight lines or Cartesian coordinates due to its curvature. The paragraph explains how the restriction of points to the sphere's surface reduces the degrees of freedom from three to two, making the co-dimension one. The need for extending tensor calculus to non-Euclidean spaces is also discussed.
🌀 The Concept of Manifolds and Their Properties
This paragraph broadens the discussion to include more abstract manifolds, such as a four-dimensional Euclidean space containing a three-dimensional non-Euclidean sub-manifold, or the space-time of general relativity. It clarifies the distinction between a manifold and space, explaining that a manifold is a topological space that locally resembles Euclidean space and is characterized by its differentiability. The concept of homeomorphism is introduced to describe the local similarity between manifolds and Euclidean spaces. The paragraph uses the analogy of mapping the Earth's surface to a flat map to illustrate the idea of deformation required for such a transformation, emphasizing that a manifold is locally flat.
📉 Demonstrating Local Flatness of Manifolds
The fourth paragraph uses a graphical example of an elliptic paraboloid to demonstrate the local flatness of manifolds. It describes the process of zooming in on a point on the surface, showing how the surface appears to flatten out as the neighborhood becomes smaller. The tangent plane and geodesic paths are introduced, and the importance of the surface being smooth, continuous, and differentiable for it to qualify as a manifold is highlighted. The summary concludes with the idea that for a space to be considered a manifold, it must be possible to find a neighborhood small enough that the surface is effectively indistinguishable from a flat plane.
🌉 Real-World Examples of Manifold Deviation
The final paragraph applies the concept of manifolds to real-world examples, starting with a quantitative analysis of the deviation from a straight line for an arc of a given radius with a chord of a certain length. It simplifies the formula for cases where the chord is much smaller than the radius, providing an approximation that is practical for small values. The paragraph then gives examples of the Lake Pontchartrain Bridge, the Brooklyn Bridge, and a pool table, illustrating how the curvature of the Earth affects their construction or levelness. It concludes by emphasizing the necessity of a space being smooth, continuous, and differentiable to be considered a manifold and hints at the upcoming in-depth analysis of smooth surfaces in the next video.
Mindmap
Keywords
💡Tensor Calculus
💡Non-Euclidean Manifolds
💡Embedded Manifold
💡Co-dimension
💡Spherical Polar Coordinates
💡Euclidean Spaces
💡Affine Coordinate System
💡Manifold
💡Homeomorphic
💡Geodesic
💡Tangent Plane
Highlights
Mastering the first 56 videos provides confidence in understanding tensor calculus for Euclidean spaces.
The upcoming analysis will extend to non-Euclidean manifolds, where tensor calculus is particularly effective.
An embedded manifold, or sub-manifold, is defined as an m-dimensional manifold within a larger in-dimensional manifold called the ambient space.
The difference in dimensionality between the manifold and sub-manifold is termed the co-dimension.
A plane serves as a simple example of an embedded manifold, illustrating the concept with a coordinate system.
A plane is a two-dimensional manifold with coordinates u and v, but also a subset of a three-dimensional space with xyz coordinates.
A plane is considered a two-dimensional sub-manifold embedded in a three-dimensional manifold, with a co-dimension of one.
Both the ambient space and the sub-manifold can be Euclidean spaces where tensor calculus applies.
The surface of a sphere is a two-dimensional non-Euclidean sub-manifold embedded in a three-dimensional Euclidean space.
Spherical coordinates theta and phi uniquely identify points on the surface of a sphere.
The coordinate lines on the surface of a sphere are circles, indicating a non-Euclidean nature.
A spiral curve is a one-dimensional sub-manifold with arc length s as its coordinate.
A manifold is a topological space that locally resembles Euclidean space, being homeomorphic to it.
A manifold is locally flat, and this property is essential for the application of tensor calculus.
The video demonstrates the concept of a manifold using an elliptic paraboloid and its tangent plane.
Manifolds must be smooth, continuous, and differentiable to qualify for tensor calculus analysis.
The video concludes with real-world examples quantifying the deviation from flatness due to Earth's curvature.
The Brooklyn Bridge and a pool table serve as examples to illustrate the practical implications of manifold theory.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: