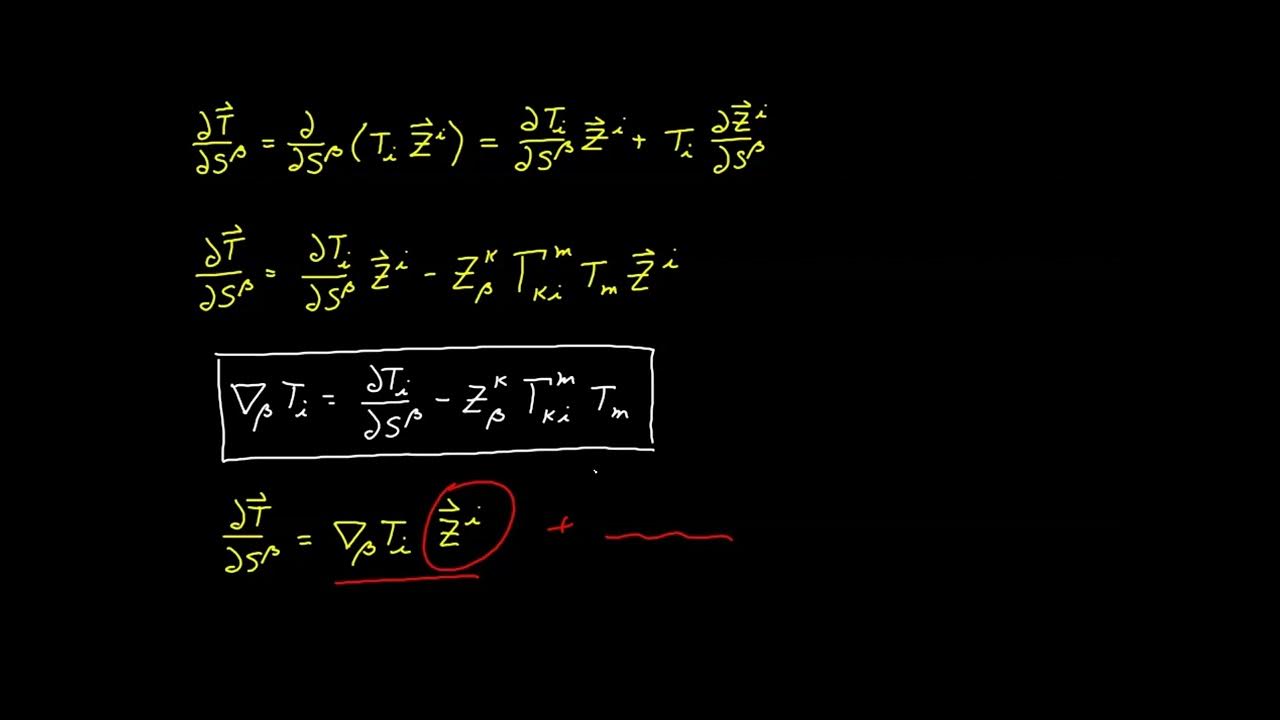Video 88 - Embedded Curves - Part 1

Tensor Calculus

5 Jun 202224:15

EducationalLearning

32 Likes 10 Comments

TLDRThis script from a tensor calculus video series shifts focus from surfaces to curves, explaining how one-dimensional sub-manifolds relate to their ambient space. It reviews surface analysis, introduces curve analysis using a single coordinate value, and parallels the concepts between the two. The video covers parametric equations, covariant and contravariant basis vectors, metric tensors, and other tensor calculus tools, emphasizing their direct application to curves. It also touches on higher dimensions and the implications for tensor analysis in various manifolds.

Takeaways

🔄 Almost everything learned from surface analysis applies to curves with minor adjustments.
📏 A curve is a one-dimensional sub-manifold within an ambient space, requiring only a single coordinate value.
🔢 In tensor calculus, curves use a generalized coordinate value 'u1,' which may include a variable scaling factor.
↔️ Covariant basis vectors for curves are always tangent to the curve and may vary in length.
🔄 Jacobian and its inverse in curve analysis resolve to ordinary derivatives due to the one-dimensional nature.
🔗 Covariant and contravariant metric tensors for curves consist of only one component, which are reciprocals of each other.
📏 The arc length (s) serves as a direct measure of the Euclidean distance along the curve.
🔄 For curves, permutation symbols always equal 1, simplifying many tensor operations.
📐 The metric equation for curves provides a direct relationship between the line element and the coordinate system.
🔁 Surface-related tensor relationships, such as the shift tensor, directly translate to curves with minimal adjustments.

Q & A

What is the primary focus shift introduced in video 88 of the series?
-The focus shifts from the analysis of surfaces (two-dimensional sub-manifolds) to the analysis of curves (one-dimensional sub-manifolds).
How is a curve defined in the context of tensor calculus?
-A curve is defined as a smooth line drawn in space that qualifies as a one-dimensional sub-manifold, requiring only a single coordinate value to describe it.
What is the advantage of using a generalized coordinate value 'u1' instead of the arc length 's' for curves?
-Using 'u1' as a generalized coordinate allows flexibility in scaling and avoids limiting the analysis to a specific coordinate system, making it easier to apply tensor calculus consistently.
Why is it beneficial to retain the free index notation in the analysis of curves?
-Retaining the free index notation helps maintain consistency with tensor calculus syntax, reminding us which objects are covariant or contravariant and aiding in understanding full contractions and invariants.
How does the covariant basis vector behave in the context of curves?
-The covariant basis vector is always tangent to the curve, though it may not be a unit vector, reflecting the curve's direction at each point.
What simplifications occur when analyzing curves using the concepts of Jacobian and its inverse?
-For curves, the Jacobian and its inverse simplify to ordinary derivatives, and any summation involving a dummy index resolves to a single term since the index must equal one.
What happens to the permutation symbol when applied to curves?
-For curves, the permutation symbol always equals one because there's only one index, which prevents duplicates or odd permutations.
How is the volume element concept adapted for curves?
-For curves, the volume element is referred to as a line element and is calculated as the square root of the determinant of the covariant metric tensor, which corresponds to the magnitude of the covariant basis vector.
What is the significance of the shift tensor in the analysis of curves?
-The shift tensor for curves allows transformation between curve components and ambient space components, similar to its role in surface analysis, but with simplified indices due to the one-dimensional nature of curves.
What is the relationship between arc length and the metric equation for curves?
-The arc length is directly related to the metric equation, with the line element acting as a scaling factor between the differential arc length 'ds' and the coordinate differential 'du1'.

Outlines

00:00

📚 Introduction to Curve Analysis in Tensor Calculus

This paragraph introduces a shift in focus from studying surfaces to analyzing curves within the context of tensor calculus. It explains that curves, as one-dimensional sub-manifolds, are analogous to surfaces in many ways. The concept of using arc length 's' as a coordinate for curves is introduced, and the idea of a generalized coordinate 'u1' is presented to maintain consistency with tensor calculus syntax. The paragraph also emphasizes that the principles discussed for surfaces will carry over to curves, with the analysis facilitated by the use of free indices for 'u'.

05:00

🔍 Curve Analysis and Higher Dimensions

The second paragraph delves into the applicability of surface analysis principles to curves, even in higher-dimensional ambient spaces. It clarifies the definition of a hypersurface and how curves, as one-dimensional sub-manifolds, differ in dimensionality and co-dimension. The paragraph further explains how the analysis of curves will be consistent with tensor calculus, with a focus on the simplification that occurs due to the single coordinate nature of curves, leading to single-term expressions for covariant and contravariant transformations, Jacobian matrices, and metric tensors.

10:02

📐 Tangent Vectors and Basis for Curves

This paragraph discusses the properties of tangent vectors and basis for curves. It describes how the covariant basis vector is always tangent to the curve, and how the contravariant basis vector, while having the same direction, can vary in magnitude. The paragraph also covers the properties of these basis vectors, the formation of linear combinations of tangent vectors, and the implications for raising and lowering indices in the context of curves. The importance of retaining index structure for understanding covariant and contravariant components is highlighted.

15:05

🌐 Permutation Symbols and Dot Products in Curve Analysis

The fourth paragraph explores permutation symbols and their relevance to curve analysis, noting that for curves, the permutation symbol is always equal to one due to the single index involved. It then transitions into discussing dot products of vectors tangent to the curve, emphasizing the importance of understanding whether the components are covariant or contravariant. The paragraph also touches on the simplification of expressions for raising and lowering indices and the determinant of a single-entry matrix in the context of curves.

20:07

📈 Volume Elements, Metric Equations, and Curve Analysis

The final paragraph of the script discusses the concept of volume elements, specifically in relation to curves, and how they relate to the magnitude of the covariant basis vector. It introduces the line element and its significance in connecting coordinate values to Euclidean distances along the curve. The paragraph also covers the metric equation for curves, the shift tensor, and how these tools can be used to convert between ambient and curve components of vectors and tensors. The summary concludes with the relationship between the line element and arc length, providing a method for calculating arc length along a curve.

Mindmap

Keywords

💡Embedded Sub-manifolds

Embedded sub-manifolds are subsets of a larger space that are themselves manifolds. In the context of the video, surfaces are two-dimensional sub-manifolds within a three-dimensional space, while curves are one-dimensional sub-manifolds. The script discusses the shift in focus from surfaces to curves, emphasizing that the analysis of curves is analogous to that of surfaces, but with one less dimension.

💡Arc Length

Arc length is the measure of the distance between two points on a curve, and it is used as a single coordinate value for curves in the script. It is a way to assign numerical values to points along a curve, directly related to the Euclidean distance from the origin. The script mentions that arc length provides a convenient way to uniquely identify locations along a curve.

💡Parametric Equations

Parametric equations are used to describe the relationship between the ambient space and the embedded sub-manifolds. For surfaces, there are three functions of two variables (s1 and s2), while for curves, there are three functions of a single variable (u1). The script uses parametric equations to illustrate the transition from surface analysis to curve analysis.

💡Covariant Basis Vector

A covariant basis vector is defined as the derivative of the position vector with respect to the coordinate value. For curves, it is always tangent to the curve, as the coordinate line is the curve itself. The script explains that the covariant basis vector is essential for understanding the tangential properties of curves.

💡Jacobian

The Jacobian matrix is the matrix of all first-order partial derivatives of a vector-valued function. In the context of curves, it becomes the ordinary derivative since there is only one coordinate. The script discusses the Jacobian and its inverse, which are crucial for transformations between coordinate systems.

💡Covariance and Contravariance

Covariance and contravariance are properties of tensors that determine how they transform under changes of coordinates. The script explains that for curves, the covariant and contravariant components are related through the metric tensor, which is a single component due to the one-dimensional nature of curves.

💡Metric Tensor

The metric tensor is a measure of the distance between points in a space and is used to define the geometry of the space. For curves, it is a single component tensor that represents the dot product of the covariant basis vector with itself. The script uses the metric tensor to derive the line element and to discuss the geometry of curves.

💡Permutation Symbols

Permutation symbols are used in tensor calculus to represent the sign of an even or odd permutation of indices. For curves, the script notes that the permutation symbol is always equal to one because there is only one index, which can only be permuted in an even way.

💡Line Element

The line element is the differential arc length along a curve, represented as ds. The script explains that the line element is related to the metric tensor and the covariant basis vector, allowing for the calculation of arc length and the unit tangent vector.

💡Shift Tensor

The shift tensor is used to transform between the components of a vector in the tangent space of a manifold and the components in the ambient space. In the script, it is shown that for curves, the shift tensor has only three elements, allowing for the transformation between the curve's tangent vector components and the ambient space.

💡Levi-Civita Symbol

The Levi-Civita symbol is a tensor used in the study of manifolds that is related to the orientation of the space. For curves, as explained in the script, the Levi-Civita symbol simplifies to either +1 or -1, depending on the orientation, because there is only one dimension to consider.

Highlights

Shift in focus from studying surfaces to analyzing curves as one-dimensional sub-manifolds.

Curves are lines within the ambient space, analogous to surfaces but with a single coordinate value.

Arc length 's' is used as a convenient coordinate for curves, directly related to Euclidean distance from the origin.

Generalized coordinate 'u1' introduced for curves, maintaining tensor calculus syntax and co- and contravariance relationships.

Parametric equations for curves have the same form as for surfaces but with a single argument.

Covariant basis vector for curves is always tangent to the curve, simplifying the analysis.

Jacobian and its inverse for curves result in ordinary derivatives, streamlining calculations.

Dummy index for curves always has the value of one, reducing summations to single terms.

Covariant and contravariant metric tensors for curves are simplified to single components due to one-dimensional nature.

Permutation symbols for curves are always equal to one, impacting determinant and tensor relationships.

Dot product of vectors tangent to the curve is simplified by the one-dimensional nature of curves.

Raising and lowering indices for curves results in single-term expressions, simplifying tensor operations.

Relative tensors and their invariant scalar values are determined by the position of indices in tensor expressions.

Volume element for curves, or line element, is derived from the square root of the covariant metric tensor's determinant.

Unit tangent vector along the curve is obtained by normalizing the covariant basis vector.

Shift tensor for curves has three elements, allowing for conversions between curve and ambient space components.

Metric equation for curves provides a direct relationship between the line element and the coordinate differential.

Arc length along the curve can be calculated using the derived metric equation.

Transcripts

Browse More Related Video

Tensor Calculus Lecture 14c: Non-hypersurfaces - Relationship Among The Shift Tensors

Video 70 - Surface Christoffel Examples

Video 72 - Surface Covariant Derivative for Non Tangent Vectors

Video 59 - Common Baseline

Video 58 - Tangent Space

Video 92 - Curves Embedded in Surfaces

Related Tags

Tensor Calculus Curve Analysis Sub-Manifolds Embedded Manifolds Arc Length Parametric Equations Covariant Basis Metric Tensor Euclidean Distance Manifold Theory Mathematics Education