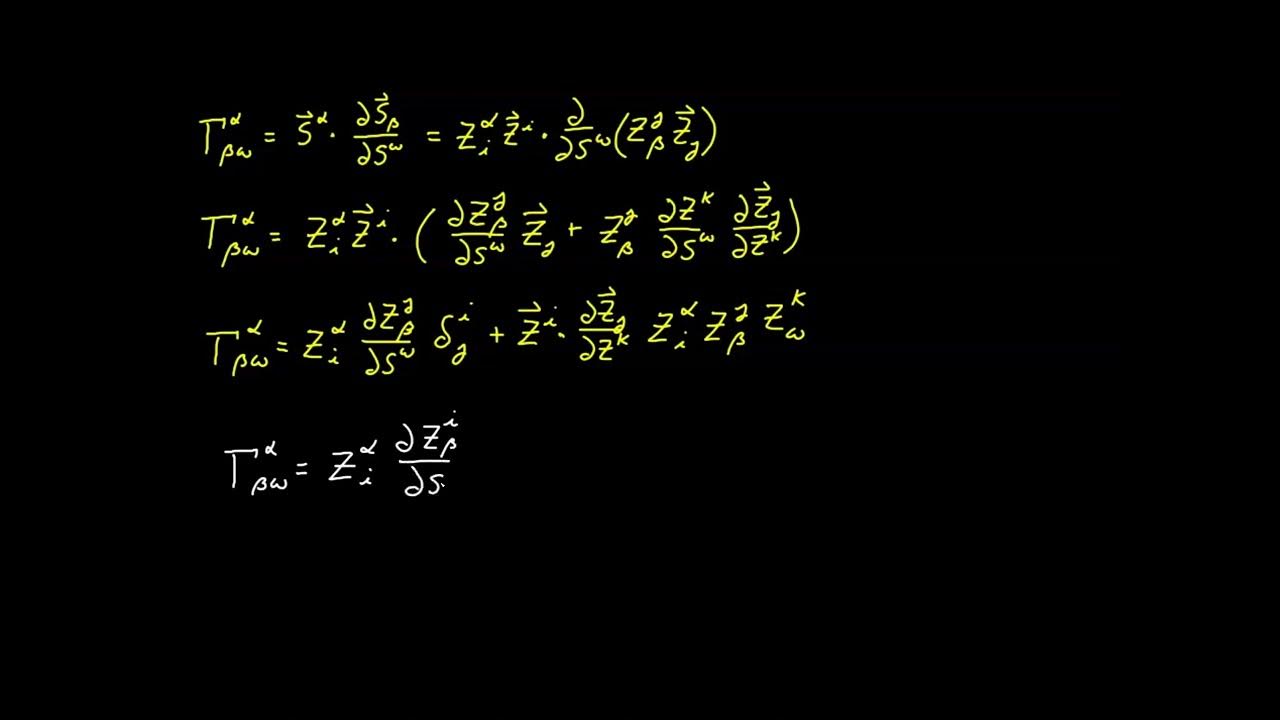Video 68 - Christoffel Symbol for Surfaces - Part 1

Tensor Calculus

5 Jun 202220:43

EducationalLearning

32 Likes 10 Comments

TLDRThis video delves into the intricacies of the Christoffel symbol in tensor calculus, particularly its application to curved surfaces and manifolds. It explains the necessity of modifying the symbol's definition to accommodate non-Euclidean spaces, introducing the curvature tensor—a second-rank, symmetric tensor that plays a crucial role in analyzing curved surfaces. The video also demonstrates how the properties of the Christoffel symbol, derived in previous episodes, remain valid due to the dot product with a contravariant basis vector, which simplifies the expression and reaffirms its utility across various manifolds.

Takeaways

📚 The Christoffel symbol, introduced in video 28, is used to form linear combinations with covariant basis vectors, representing the partial derivative of a covariant basis vector with respect to a coordinate value.
🛠️ The Christoffel symbol works in Euclidean spaces and for flat planes, but modifications are needed for curved surfaces and manifolds.
🌀 To understand the necessary changes for curved surfaces, consider the derivative of a covariant basis vector along a coordinate line, which introduces a normal component not present in Euclidean spaces.
🔄 On curved surfaces, the partial derivative of a basis vector may produce a vector that doesn't lie in the tangent plane, necessitating an extra term for the normal component in its representation.
📐 This additional term, which includes a scalar value for the normal direction change, is essential for accurately representing vectors on curved surfaces.
🌟 The new factor, known as the curvature tensor, is a second-rank covariant tensor that is symmetric in its indices.
🔍 The curvature tensor plays a pivotal role in analyzing curved surfaces, appearing in future analyses.
🔑 The Christoffel symbol remains valid for all manifolds when defined using the derived relationship, but its application differs between Euclidean and surface projections.
📝 For a plane, the curvature tensor equals zero, while the general expression for a surface manifold includes it.
🔗 The properties of the Christoffel symbol derived in earlier videos (transformation rules, first and second kinds, and metric tensor relationships) remain applicable to curved surfaces due to the consistent form of the symbol.

Q & A

What is the main focus of this video in the series on tensor calculus?
-The main focus of this video is to examine the Christoffel symbol and to understand how its definition needs to be modified for it to be applicable to surfaces and curved manifolds.
What is the Christoffel symbol used for in tensor calculus?
-The Christoffel symbol is used in conjunction with covariant basis vectors to form linear combinations that represent the partial derivative of a covariant basis vector with respect to a coordinate value.
Why is the simple form of the Christoffel symbol not sufficient for all surfaces?
-The simple form of the Christoffel symbol is not sufficient for all surfaces because it does not account for the normal component that arises when dealing with curved surfaces, which may result in a vector that is not in the tangent plane.
What is the significance of the curvature tensor in the context of this video?
-The curvature tensor plays a pivotal role in the analysis of curved surfaces, as it represents the magnitude of the change of the vector in the normal direction and is introduced to ensure the Christoffel symbol is applicable to curved surfaces.
How does the curvature tensor relate to the symmetry of the Christoffel symbol?
-The curvature tensor is a second-rank covariant tensor with symmetric indexes, meaning that it maintains the symmetry of the Christoffel symbol when the indexes are switched.
What is the special case for the curvature tensor when dealing with a plane?
-For a plane, the curvature tensor is zero, which means that the additional term introduced for curved surfaces is not needed, and the simple form of the Christoffel symbol is sufficient.
How does the dot product of the modified Christoffel symbol equation with a contravariant basis vector simplify?
-The dot product simplifies by canceling out the normal component, as the basis vectors are orthogonal to the normal, and results in an expression that is identical to the one derived for the Christoffel symbol in the context of a plane.
Why is the result of the dot product significant for the properties of the Christoffel symbol?
-The result of the dot product is significant because it shows that the properties derived for the Christoffel symbol in previous videos remain valid for curved surfaces, as the form is the same as the one used in the analysis for a plane.
What does the video suggest for the definition of the Christoffel symbol moving forward?
-The video suggests that the definition of the Christoffel symbol should be thought of in terms of the relationship derived from the dot product, which is the same for all manifolds, but with an understanding that its application differs between Euclidean space and curved surfaces.
What will be the focus of the next video in the series?
-The next video will continue the analysis of the Christoffel symbol, specifically in relation to its application to surfaces and curved manifolds, building on the insights gained from the current video.

Outlines

00:00

📚 Introduction to the Christoffel Symbol and its Modification for Curved Manifolds

This paragraph introduces the Christoffel symbol, a set of scalar functions used in tensor calculus, specifically for surfaces and curved manifolds. It explains that while the symbol was initially defined for Euclidean spaces and works for flat planes, it must be modified for general curved surfaces. The modification involves adding a term to account for vectors that may not lie in the tangent plane. The paragraph also discusses the graphical interpretation of taking the partial derivative of a covariant basis vector with respect to a coordinate value, highlighting the need for the Christoffel symbol to be redefined to accommodate the normal component introduced by the curvature.

05:00

🔍 The Curvature Tensor: Extending the Christoffel Symbol for Curved Surfaces

The second paragraph delves into the necessity of extending the Christoffel symbol for curved surfaces by introducing the curvature tensor, denoted as b_alpha_beta. It explains that the curvature tensor is a second-rank covariant tensor that plays a crucial role in the analysis of curved surfaces. The paragraph discusses the properties of the curvature tensor, including its symmetry and the fact that it is zero for a flat plane, indicating that the tensor is essential for representing the normal component of the vector change in the tangent space.

10:01

📐 Deriving the Curvature Tensor and its Properties

This paragraph focuses on deriving the basic properties of the curvature tensor. It uses the quotient theorem to establish that the tensor is indeed a tensor due to its ability to transform a known vector into another vector. The paragraph also discusses the symmetry of the tensor's indices, which is a result of the symmetry in the partial derivatives of the covariant basis vectors. The conclusion is that the curvature tensor is a second-rank covariant tensor with symmetric indices, and its value is zero for a plane, making it a special case of the general expression for a surface manifold.

15:01

🔄 The Dot Product and the Explicit Form of the Christoffel Symbol

The fourth paragraph describes the process of taking the dot product of both sides of the modified Christoffel symbol equation with a contravariant basis vector. This operation simplifies the equation by eliminating the normal component due to the orthogonality of the basis vectors and the normal. The result is an explicit form of the Christoffel symbol for the surface, which is identical to the form derived in previous videos for Euclidean spaces. This consistency allows for the properties and derivations from previous analysis to be applied to the surface case without modification.

20:02

🔗 Continuity of the Christoffel Symbol Analysis and Future Directions

The final paragraph summarizes the key takeaways from the video, emphasizing that the analysis of the Christoffel symbol from previous videos remains valid despite the need to modify its definition for curved manifolds. It highlights the continuity of the symbol's properties and the importance of understanding its different applications in Euclidean space versus on a surface. The paragraph concludes by setting the stage for further exploration of the Christoffel symbol in relation to surfaces and curved manifolds in upcoming videos.

Mindmap

Keywords

💡Christophel Symbol

The Christophel symbol is a set of scalar functions used in differential geometry to describe how basis vectors change as one moves through a curved space. In the video, it is discussed that the definition of the Christophel symbol needs to be modified for its applicability to curved manifolds, not just Euclidean spaces. The script mentions that the Christophel symbol plays a crucial role in forming linear combinations with covariant basis vectors, and its modification is necessary to account for vectors that may not lie in the tangent plane of a curved surface.

💡Covariant Basis Vectors

Covariant basis vectors are tangent vectors to a manifold that form a basis for the tangent space at each point. The video script explains that these vectors are used in conjunction with the Christophel symbol to represent changes in direction along coordinate lines on a curved surface. An example from the script is the graphical illustration of how a covariant basis vector must remain tangent to a curving coordinate line, necessitating a change in direction.

💡Partial Derivative

A partial derivative is a derivative of a function of multiple variables with respect to one of those variables, while the others are held constant. In the context of the video, the partial derivative of a covariant basis vector with respect to a coordinate value is discussed, which is essential for understanding how the basis vector changes direction as it moves along a coordinate line on a curved surface.

💡Euclidean Space

Euclidean space is a mathematical setting in which the geometry is defined by the distance formula and the angle between vectors. The script mentions that the original form of the expression for the Christophel symbol is valid for Euclidean spaces, which includes simple planes, but modifications are required for it to be applicable to more general curved surfaces.

💡Curvature Tensor

The curvature tensor is introduced in the script as a new term necessary for the modified definition of the Christophel symbol to work on curved surfaces. It is a second-rank covariant tensor that accounts for the change in direction of a vector that is not confined to the tangent plane of the surface. The script explains that the curvature tensor is pivotal in the analysis of curved surfaces and has symmetric properties.

💡Tangent Plane

The tangent plane is a concept in differential geometry where, at each point on a surface, there exists a flat plane that best approximates the surface at that point. The video script discusses how the basis vectors must lie in the tangent plane and how the introduction of the curvature tensor helps represent vectors that may not lie entirely in this plane.

💡Surface Projection

Surface projection refers to the component of a vector that lies in the tangent plane of a surface. In the video, it is mentioned that when the surface is curved, the change in direction of a basis vector may introduce a component that is not in the tangent plane. The concept is used to explain the need for modification in the expression for the Christophel symbol to include both surface and normal projections.

💡Normal Component

The normal component of a vector is the part of it that is perpendicular to the tangent plane of a surface. The script explains that when dealing with curved surfaces, the change in a basis vector's direction can introduce a normal component, which must be accounted for in the modified definition of the Christophel symbol.

💡Quotient Theorem

The quotient theorem is a mathematical principle used to determine whether a quotient of tensors is also a tensor. In the script, the quotient theorem is applied to demonstrate that the curvature tensor is indeed a tensor, by showing that the quotient of a vector by a non-zero vector results in another tensor.

💡Symmetric Tensor

A symmetric tensor is one where the order of its indices does not affect its value. The script discusses the symmetry of the curvature tensor, indicating that interchanging the indices alpha and beta does not change the tensor's value, which is an important property for its application in the analysis of curved surfaces.

💡Manifold

A manifold is a topological space that locally resembles Euclidean space near each point. The video script uses the term to describe both flat (plane) and curved surfaces, emphasizing that the definition and application of the Christophel symbol must be adjusted depending on whether the manifold is flat or curved.

Highlights

Introduction of the need to modify the definition of the Christoffel symbol for general applicability to surfaces and curved manifolds.

Explanation of the Christoffel symbol as a set of scalar functions used with covariant basis vectors to form linear combinations.

Clarification that the simple form of the Christoffel symbol is valid for Euclidean spaces and flat planes but not for all curved surfaces.

Graphical representation of a curved surface to illustrate the concept of taking the partial derivative of a covariant basis vector.

Discussion on the limitations of the Christoffel symbol's simple form when dealing with vectors that may not lie in the tangent plane.

Introduction of the curvature tensor, denoted as b_alpha_beta, as a necessary extension for the Christoffel symbol to work with curved surfaces.

Derivation of the curvature tensor as a second-rank covariant tensor with symmetric indexes.

Identification of the curvature tensor's role in representing the normal component of a vector change on a curved surface.

Demonstration that the curvature tensor equals zero for a plane manifold, making it a special case.

Dot product operation with the contravariant basis vector to derive an explicit relationship for the Christoffel symbol on a surface.

Revelation that the derived form of the Christoffel symbol for a surface is identical to the form derived in previous videos for Euclidean spaces.

Conclusion that previous derivations and properties of the Christoffel symbol apply equally to both Euclidean and curved spaces.

Explanation of the different application of the Christoffel symbol for Euclidean space versus curved surfaces.

Emphasis on the importance of the curvature tensor in the analysis of curved surfaces and its frequent appearance in future discussions.

Review of the video's content, summarizing the modifications made to the Christoffel symbol and the introduction of the curvature tensor.

Preview of continuing the analysis of the Christoffel symbol in relation to surfaces and curved manifolds in the next video.

Transcripts

Browse More Related Video

Video 69 - Christoffel Symbol for Surfaces - Part 2

Video 29 - Christoffel Symbol Transformation

Video 59 - Common Baseline

Tensor Calculus Lecture 8: Embedded Surfaces and the Curvature Tensor

Tensor Calculus 6a: The Christoffel Symbol

Video 70 - Surface Christoffel Examples

Related Tags

Tensor Calculus Christoffel Symbol Curvature Tensor Euclidean Space Covariant Basis Partial Derivative Surface Manifold Geometry Analysis Mathematics Education Advanced Concepts