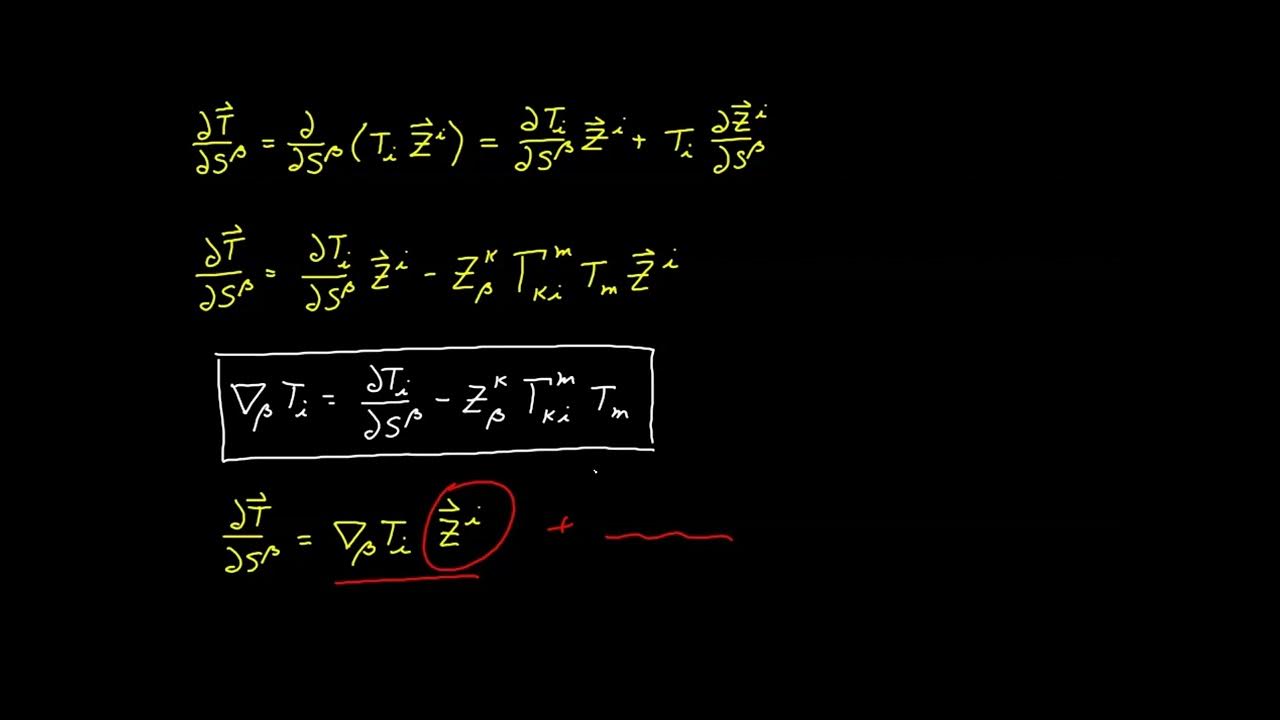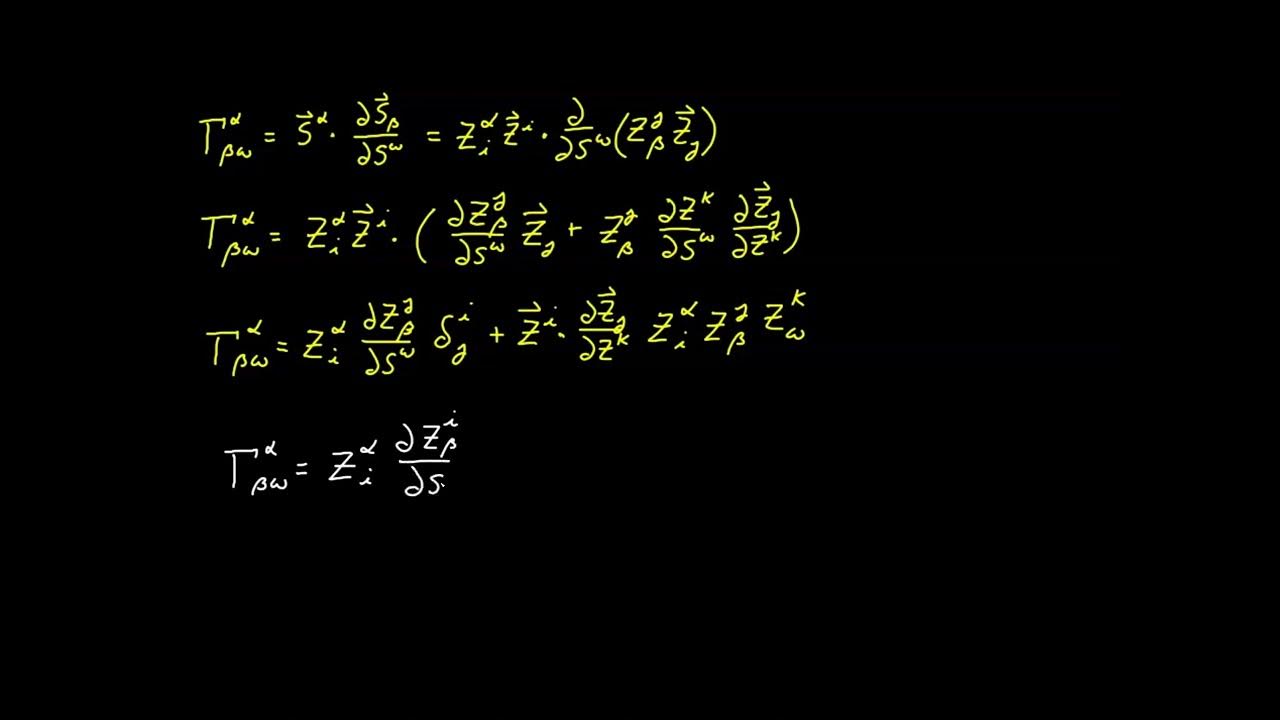Video 62 - Embedded Curve
TLDRThis video introduces the concept of an embedded curve within a surface, deriving expressions for the metric equation and arc length in terms of surface coordinates. It explores the relationship between ambient and surface covariant metric tensors using shift tensors, simplifying calculations in non-Euclidean manifolds. The practical value of using surface coordinates over ambient coordinates for easier computation is highlighted, with examples including cylindrical, spherical, and torus surfaces, emphasizing the universality of these concepts beyond Euclidean spaces.
Takeaways
- 📚 The video introduces the concept of an embedded curve and its relation to tensor calculus, specifically focusing on metric equations and arc length in surface coordinates.
- 🌐 The script discusses curves that are not only through space but also lie on a surface, emphasizing the relationship between one-dimensional and two-dimensional manifolds.
- 🔍 The video revisits the metric equation and arc length expressions derived in a previous video, highlighting their relevance to both Euclidean and non-Euclidean spaces.
- 📈 The script explains how to derive the surface covariant metric tensor using the ambient covariant metric tensor and the shift tensor.
- 📝 The process involves taking the dot product of surface covariant basis vectors and utilizing the shift tensor to express the ambient covariant metric tensor.
- 🧩 The video demonstrates the relationship between the curve parameterized on the surface and the same curve in ambient coordinates, using the shift tensor.
- ✂️ By multiplying through by dt, the script derives the differential form that relates the surface differential to the ambient differential.
- 📐 The script shows how to use the derived expressions to write the metric equation for the surface and calculate the arc length in a simpler form using surface coordinates.
- 📉 The video points out that using surface coordinates generally results in fewer terms and a simpler calculation compared to using ambient coordinates.
- 🌍 Practical examples are given for cylindrical, spherical, and torus surfaces, illustrating how to apply the metric equations and calculate arc lengths.
- 🔚 The video concludes by emphasizing the utility of the shift tensor in relating covariant metric tensors between ambient and surface perspectives and the importance of choosing the correct coordinate system for simplification.
Q & A
What is the main topic of this video in the series on tensor calculus?
-The main topic of this video is the concept of an embedded curve and deriving expressions for the metric equation and arc length in terms of surface coordinates.
What is an embedded curve in the context of this video?
-An embedded curve is a one-dimensional manifold that lies on the surface of a two-dimensional manifold, meaning every point on the curve is also a point on the surface.
Why are the expressions for the metric equation and arc length important in this context?
-The expressions for the metric equation and arc length are important because they allow us to understand how to measure distances and curvature on a surface that is embedded within a higher-dimensional space.
What is the significance of the shift tensor in this video?
-The shift tensor is significant because it is used to relate the basis vectors between the ambient and sub-manifold spaces and to derive the relationship between the covariant metric tensors.
How does the video script connect the concept of an embedded curve to the metric equation?
-The script connects the concept by showing that the surface covariant metric tensor can be derived in terms of the ambient covariant metric tensor using a combination of shift tensor factors.
What is the practical value of using surface coordinates instead of ambient coordinates when calculating arc length?
-Using surface coordinates simplifies the calculation because it reduces the number of terms in the integral, making it easier to evaluate compared to using ambient coordinates.
Why does the script mention that the results derived for Euclidean spaces also apply to non-Euclidean spaces?
-The script mentions this to highlight the general applicability of the concepts and equations developed throughout the series, emphasizing that they are not limited to Euclidean spaces.
What is the difference between the arc length of a curve and the surface coordinates mentioned in the script?
-The arc length of a curve is the measure of distance along the curve, while the surface coordinates are the parameters that map out the surface on which the curve is embedded.
How does the script demonstrate the relationship between the ambient and surface differentials?
-The script demonstrates this by showing that the differential of the curve's coordinates in ambient space can be related to the differential in surface space through the use of the shift tensor.
What are some examples of surfaces for which the metric equations are derived in the script?
-The script derives metric equations for cylindrical, spherical, and torus surfaces, showing how the process is straightforward once the non-zero elements of the covariant metric tensor are identified.
Outlines
📚 Introduction to Embedded Curves and Metric Equations
This paragraph introduces the concept of an embedded curve within the context of tensor calculus. It explains how a curve can be embedded on a surface, creating a one-dimensional manifold within a two-dimensional manifold, both of which are non-Euclidean. The paragraph also revisits the metric equation and arc length expressions derived in a previous video, and sets the stage for deriving these expressions in terms of surface coordinates. The importance of the shift tensor in relating the basis vectors of the ambient and sub-manifold is highlighted.
🔍 Deriving Surface Covariant Metric Tensor and Arc Length
The second paragraph delves into the derivation of the surface covariant metric tensor using the shift tensor and the ambient covariant metric tensor. It explains the process of finding the dot product of the surface covariant basis vectors and how this leads to the metric tensor expression. The paragraph also discusses the differential form of the curve's position vector in terms of the surface coordinates and the shift tensor, ultimately leading to a new expression for the arc length that can be calculated using either ambient or surface values.
📉 Simplification of Calculations Using Surface Coordinates
This paragraph emphasizes the practical value of using surface coordinates over ambient coordinates when calculating arc lengths. It illustrates that the surface coordinate approach simplifies the expression due to the reduced number of terms, as the curve is constrained to the surface, thus reducing the degrees of freedom from three to two. The paragraph also provides a comparative analysis of the complexity of the expressions in both ambient and surface perspectives, advocating for the use of surface coordinates for simpler calculations.
🌐 Applying Metric Equations to Sample Surfaces
The final paragraph demonstrates the application of the derived metric equations to specific sample surfaces, such as the cylindrical, spherical, and taurus surfaces. It shows the straightforward process of calculating the metric equations and arc lengths for these surfaces by using their respective covariant metric tensors. The paragraph concludes by reiterating that the results obtained are consistent with those from previous videos, highlighting the universality of the derived formulas across different manifolds, and not just limited to Euclidean spaces.
Mindmap
Keywords
💡Embedded Curve
💡Metric Equation
💡Arc Length
💡Surface Coordinates
💡Covariate Basis Vectors
💡Shift Tensor
💡Ambient Space
💡Submanifold
💡Differential Form
💡Euclidean Spaces
Highlights
Introduction of the concept of an embedded curve in tensor calculus.
Derivation of expressions for the metric equation and arc length in terms of surface coordinates.
Explanation of the curve as a one-dimensional manifold embedded in a two-dimensional manifold.
Discussion of the non-Euclidean nature of both the curve and surface manifolds.
Exploration of the dot product of surface covariant basis vectors using the shift tensor.
Derivation of the surface covariant metric tensor in terms of the ambient covariant metric tensor.
Expression of the curve's coordinates as a function of surface coordinates and the parameter t.
Use of the shift tensor to relate the covariant metric tensors between ambient and surface perspectives.
Development of a differential form relating the surface differential to the ambient differential.
Re-expression of the arc length formula using surface coordinates for simplicity.
Comparison of the practical value of using surface coordinates versus ambient coordinates for calculation.
Illustration of the reduction in degrees of freedom when working with embedded curves on surfaces.
Application of the derived formulas to calculate the metric equation and arc length for cylindrical surfaces.
Application of the derived formulas to spherical and toroidal surfaces.
Demonstration of the utility of the shift tensor in various tensor calculus applications.
Reinforcement of the concept that the results derived for Euclidean spaces apply to non-Euclidean spaces as well.
Conclusion emphasizing the practicality of using surface coordinates for simpler calculations in tensor calculus.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: