Tensor Calculus Lecture 8: Embedded Surfaces and the Curvature Tensor
TLDRThis lecture delves into the concept of embedded surfaces and the curvature tensor, essential for understanding the intrinsic properties of curved spaces. Starting with the basics, it introduces covariant and contravariant metric tensors, Christoffel symbols, and covariant derivatives. The focus then shifts to the curvature tensor's emergence due to the surface's inability to decompose vectors in the tangential plane, highlighting its significance in capturing the essence of curvature. The lecture concludes with the definition of mean curvature, a key invariant property, demonstrating the natural progression from Euclidean spaces to more complex manifolds.
Takeaways
- 📚 The lecture introduces the concept of embedded surfaces and the curvature tensor, which are fundamental in understanding the properties of surfaces in a three-dimensional Euclidean space.
- 🔍 The instructor emphasizes the importance of reviewing past lectures on fundamental objects in Euclidean space, Christoffel symbols, and covariant derivatives to better understand the curvature tensor.
- 📐 The concept of a covariant basis is explained, which is derived by differentiating the position vector with respect to surface coordinates, and is essential for defining the tangential plane to the surface.
- 📏 The covariant metric tensor is introduced through the dot product of the covariant basis elements, allowing for the measurement of lengths, areas, and other geometric properties on the surface.
- 📉 The contravariant metric tensor is defined as the inverse of the covariant metric tensor, which is crucial for index raising and lowering in tensor operations.
- 🧭 The unit normal vector to the surface is discussed, which is orthogonal to the covariant basis and is vital for defining the curvature properties of the surface.
- 🔄 The Christoffel symbols are redefined in the context of embedded surfaces, highlighting the intrinsic nature of these symbols and their dependence on the metric tensor and its derivatives.
- 🚫 The script points out the limitations of the Euclidean space approach when dealing with curved surfaces, indicating that the covariant derivative of the covariant basis is not necessarily zero due to curvature.
- 🔑 The curvature tensor is introduced as a result of the non-zero covariant derivative of the covariant basis, which is proportional to the normal vector with coefficients that define the curvature tensor.
- 📊 Mean curvature is defined as the contraction of the curvature tensor, providing a scalar measure of the curvature of the surface that is invariant under coordinate transformations.
- 🎯 The lecture concludes with the promise that understanding of curvature is within reach, emphasizing the natural emergence of the curvature tensor from the properties of embedded surfaces.
Q & A
What is the main topic of the lecture?
-The main topic of the lecture is embedded surfaces and the curvature tensor in the context of differential geometry.
Why is the lecturer eager to discuss the topic of curvature?
-The lecturer is eager to discuss curvature because the students have shown a keen interest in understanding it, and the lecturer believes their understanding of curvature is just ten minutes away.
What prerequisite knowledge is recommended for understanding the lecture?
-It is recommended to review past lectures on fundamental objects in Euclidean space, the electron Christoffel symbols, and the concept of covariant derivatives.
What is an embedded surface?
-An embedded surface is a two-dimensional surface that is embedded within a three-dimensional Euclidean space.
What are the coordinates used to map the embedded surface?
-The two coordinates used to map the embedded surface are denoted as s1 and s2.
What is the significance of the position vector R in the context of the lecture?
-The position vector R is significant as it represents an invariant field in the ambient space, which is restricted to the surface for the purpose of the lecture.
What is the covariant basis and how is it defined?
-The covariant basis is defined by differentiating the position vector with respect to each of the surface coordinates, resulting in tangential vectors to the surface.
Why can't the covariant derivative of the covariant basis be decomposed with respect to the covariant basis itself?
-The covariant derivative of the covariant basis cannot be decomposed with respect to the covariant basis because the derivative lies in the overall ambient space and not just within the tangential plane of the surface.
What is the Christoffel symbol and why is it important?
-The Christoffel symbol is a measure of how the covariant basis changes with respect to the coordinates on the surface. It is important for defining the covariant derivative and capturing the intrinsic nature of the surface's curvature.
What is the curvature tensor and how does it arise?
-The curvature tensor arises when the covariant derivative of the covariant basis is found to be proportional to the normal vector with certain coefficients of proportionality. These coefficients are the components of the curvature tensor, which is a measure of the surface's curvature.
What is mean curvature and how is it defined?
-Mean curvature is a measure of the average curvature of a surface, defined as the trace of the curvature tensor, obtained by contracting the tensor's indices using the metric tensor.
Outlines
📚 Introduction to Embedded Surfaces and Curvature Tensor
The script begins with an introduction to embedded surfaces and the curvature tensor, acknowledging that some topics have been skipped but will be backfilled later. The focus is on the concept of curvature, which is deemed essential and will be covered in several lectures. The speaker promises a brief introduction to the curvature tensor, which is eagerly anticipated by students. The prerequisites for understanding the lecture include a review of fundamental objects in Euclidean space, the Christoffel symbols, and the covariant derivative. The concept of an embedded surface in a three-dimensional Euclidean space is introduced, with the surface requiring two coordinates, s1 and s2, to be mapped.
📐 Position Vector and Covariant Basis on Embedded Surfaces
The script continues with the concept of the position vector, which is an invariant field in the ambient space, and its restriction to the surface. The position vector R is now considered as a function of the surface coordinates s1 and s2. The covariant basis is defined by differentiating the position vector with respect to each variable, resulting in tangent vectors to the surface. The script also introduces the unit normal vector n, which is orthogonal to the covariant basis vectors and has a unit length. The importance of the normal vector in defining the tangential plane to the surface is highlighted.
📏 Covariant Metric Tensor and Contravariant Basis
The third paragraph delves into the formation of the covariant metric tensor through the dot product of the covariant basis elements. The metric tensor's role in measuring lengths, areas, and volumes on the surface is mentioned. The contravariant basis is introduced as the inverse of the covariant metric tensor, and the script provides an example using spherical coordinates to illustrate the covariant metric tensor's form. The importance of the metric tensor in various calculations on the surface is emphasized.
🔍 Christoffel Symbols and the Impact of Curvature
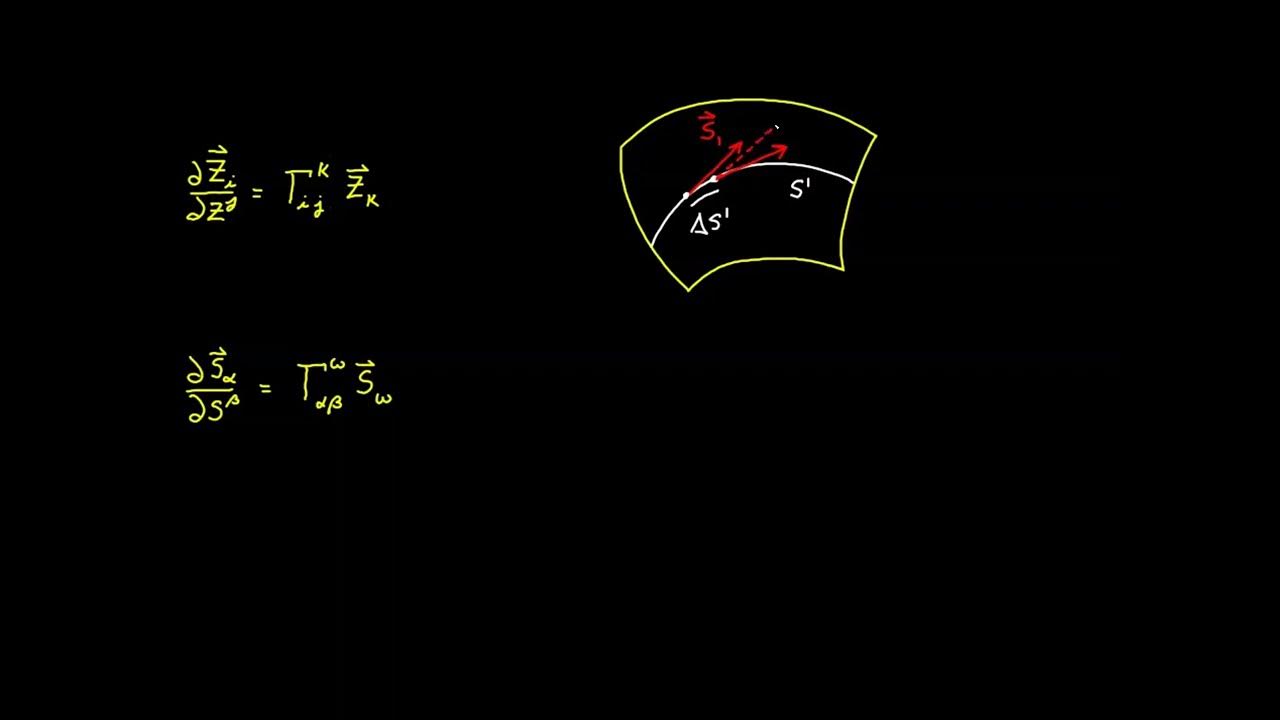
The script discusses the definition of Christoffel symbols, which are crucial for defining the covariant derivative. An attempt is made to define the Christoffel symbols using the covariant basis, but the presence of curvature introduces a problem, as the derivative of the covariant basis does not lie within the tangent plane. The script explains that this issue is a direct result of the surface's curvature and hints at the need for a new concept to address this problem.
🌐 Intrinsic and Extrinsic Approaches to Define Christoffel Symbols
The speaker presents two equivalent methods to define Christoffel symbols on surfaces, one intrinsic to the metric tensor and the other extrinsic, which uses the covariant basis. The intrinsic method relies on the metric tensor's derivatives, while the extrinsic approach maintains geometric intuition by working with the covariant basis. Both methods are shown to be valid for defining the Christoffel symbols and, by extension, the covariant derivative.
📉 Curvature's Role in the Covariant Derivative of the Basis
The script explores the covariant derivative's properties when applied to the covariant basis on a surface. It contrasts this with the Euclidean space, where the covariant derivative of the basis yields zeros. Due to curvature, the covariant derivative of the basis vectors on a surface is not zero and is instead proportional to the normal vector, with coefficients of proportionality denoted by D alpha beta. This observation leads to the introduction of the curvature tensor.
🌟 Mean Curvature and Tensor Framework
The final paragraph introduces the concept of mean curvature as a contraction of the curvature tensor, which has been identified as a natural consequence of the surface's curvature. The script emphasizes the tensor framework's ability to juggle indices and the symmetric properties of the curvature tensor. The mean curvature is presented as an important invariant property of the surface, derived from the curvature tensor.
Mindmap
Keywords
💡Embedded Surfaces
💡Curvature Tensor
💡Covariant Basis
💡Metric Tensor
💡Christoffel Symbols
💡Covariant Derivative
💡Mean Curvature
💡Tangential Plane
💡Normal Vector
💡Tensor Framework
Highlights
Introduction to embedded surfaces and the curvature tensor, a topic eagerly anticipated by students.
Acknowledgment of skipped topics with a promise to backfill them later.
Emphasis on the importance of understanding the concept of curvature in the study of embedded surfaces.
Recommendation to review past lectures on fundamental objects in Euclidean space and Christoffel symbols.
Introduction of the covariant basis and its role in defining the curvature tensor.
Explanation of the position vector R as a function of surface coordinates s1 and s2.
Differentiation of the position vector to define the covariant basis elements.
Discussion on the tangential nature of the covariant basis vectors to the embedded surface.
Introduction of the unit normal vector n and its orthogonality to the covariant basis.
Formation of the covariant metric tensor through the dot product of covariant basis elements.
Definition of the contravariant metric tensor as the inverse of the covariant metric tensor.
Mention of the curvature tensor arising from the failure of the covariant derivative of the covariant basis to be zero.
Intrinsic definition of the Christoffel symbol using the covariant derivatives of the metric tensor.
Extrinsic approach to define the Christoffel symbol using the covariant basis, despite the presence of curvature.
Introduction of the curvature tensor as a result of the covariant derivative of the covariant basis not being zero.
Explanation of the mean curvature as a contraction of the curvature tensor.
Discussion on the metronomic property of the covariant derivative with respect to the metric tensor.
Conclusion summarizing the introduction of curvature concepts and their significance in understanding embedded surfaces.
Transcripts
Browse More Related Video
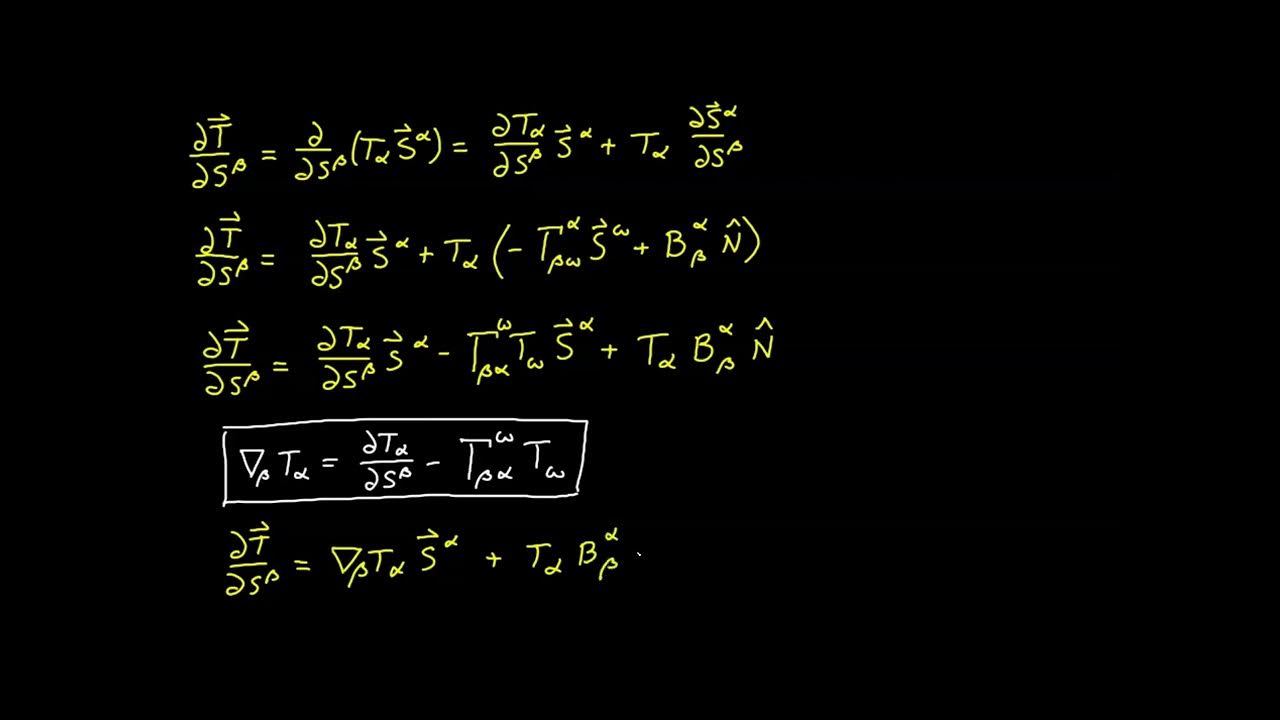
Video 71 - Surface Covariant Derivative for Tangent Vectors
Tensor Calculus Lecture 6c: The Covariant Derivative 2
Video 68 - Christoffel Symbol for Surfaces - Part 1

Tensor Calculus Lecture 8e: The Riemann Christoffel Tensor & Gauss's Remarkable Theorem

Video 89 - Curve Projections

Tensor Calculus Lecture 14c: Non-hypersurfaces - Relationship Among The Shift Tensors
5.0 / 5 (0 votes)
Thanks for rating: