Video 59 - Common Baseline

Tensor Calculus
6 Sept 202313:24
EducationalLearning
32 Likes 10 Comments

TLDRIn this Tensor Calculus video, the instructor revisits foundational concepts, emphasizing their universality across all manifolds, including non-Euclidean ones. The video serves as a baseline for further exploration into unique cases of curved surfaces. It covers covariant and contravariant basis vectors, transformations, metric tensors, and tensor algebra, highlighting their applicability to both Euclidean and non-Euclidean spaces. The instructor also touches on advanced topics like raising and lowering indices, dot products, and determinants, reinforcing the idea that most of the previously discussed concepts remain valid in any manifold.

Takeaways
  • 📚 The video script reviews previous tensor calculus concepts and emphasizes their universal applicability to all manifolds, not just Euclidean spaces.
  • 🌐 It discusses the transition from three-dimensional to two-dimensional surface coordinates, highlighting the relevance to curved surfaces.
  • 🔍 Reference numbers are provided to guide viewers back to the original videos where concepts were first derived, ensuring a deeper understanding of their application to curved manifolds.
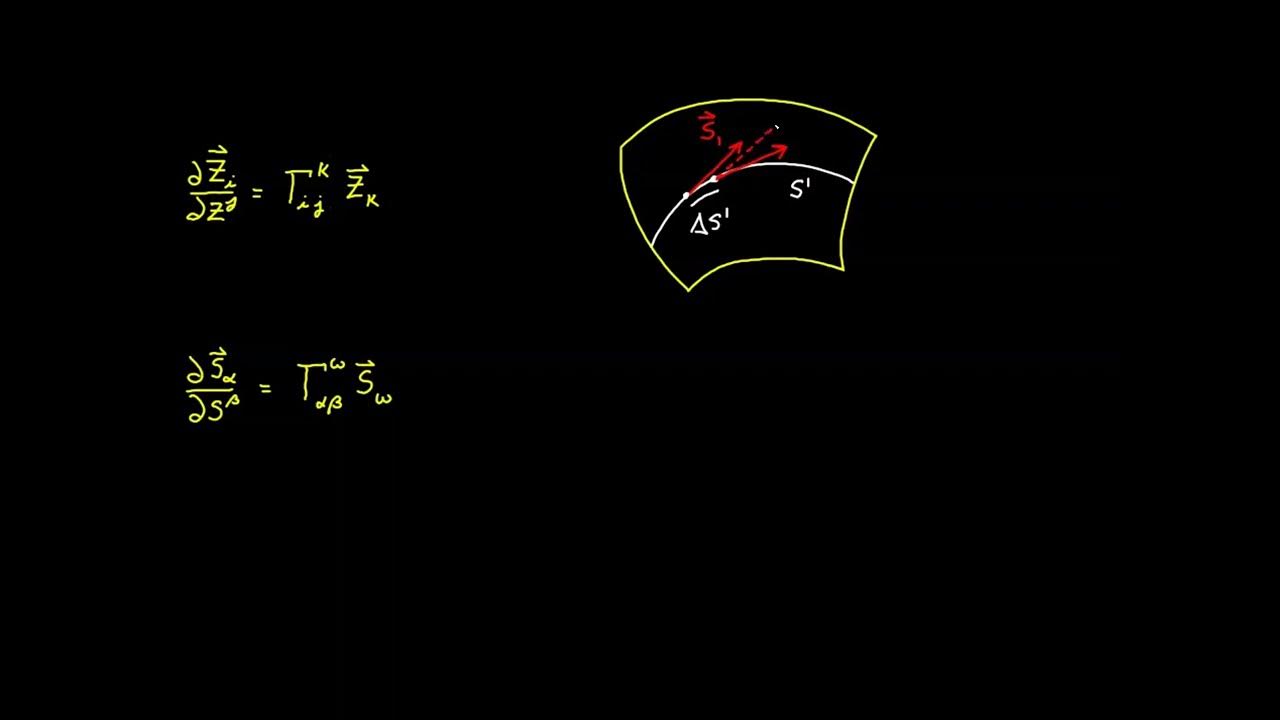
  • 📈 The script explains that covariant basis vectors can be derived using partial derivatives of the position vector, applicable to both Euclidean and non-Euclidean spaces.
  • 🔄 The concept of transformation between coordinate systems is introduced, with the Jacobian matrix playing a crucial role in these transformations.
  • 🔄🔄 The script clarifies the difference between covariant and contravariant transformations, with the free index position determining the type of transformation.
  • 📏 The covariant and contravariant metric tensors are defined, with the contravariant tensor being the inverse of the covariant tensor, a concept valid for curved surfaces.
  • 📐 The script establishes that the contravariant basis vector lies in the tangent plane, ensuring that all linear combinations formed with it also lie within the tangent plane.
  • 🔢 The properties of tensor algebra, such as addition, scalar multiplication, and tensor products, are confirmed to be universally applicable.
  • 📈🔄 The concept of raising and lowering indices using metric tensors is discussed, a technique that remains valid in non-Euclidean manifolds.
  • 📐🔄 The script touches on the dot product of vectors in the tangent plane, which remains a valid operation in curved spaces.
  • 📚🔄 The video concludes by reinforcing that all concepts covered in the first 26 videos of the series are universally applicable, setting a solid foundation for further exploration of non-Euclidean manifolds.
Q & A

  • What is the main focus of video 59 in the tensor calculus series?

    -The main focus of video 59 is to review previous results and establish that they are universally applicable to all manifolds, including both Euclidean and non-Euclidean spaces, as a foundation for exploring manifold-specific topics.

  • Why is it important to understand the covariant basis vectors derived in video 9?

    -Understanding covariant basis vectors is crucial because they form the foundation for establishing linear combinations of vectors in the tangent plane, which is essential for further tensor calculus on curved surfaces.

  • What is the significance of the Jacobian matrix in tensor calculus?

    -The Jacobian matrix is significant as it represents the transformation between different coordinate systems and is used to define covariant and contravariant transformations, which are essential for tensor operations in different coordinate systems.

  • How does the covariant metric tensor relate to the contravariant metric tensor?

    -The contravariant metric tensor is defined as the inverse of the covariant metric tensor. The contraction of these two tensors gives the Kronecker delta, which is used to define the basis vectors in the tangent plane.

  • What is the difference between covariant and contravariant transformations?

    -Covariant transformations have the free index at the bottom, while contravariant transformations have the free index at the top. These transformations are essential for tensor operations in different coordinate systems.

  • Why are the concepts of tensor algebra still valid in non-Euclidean manifolds?

    -The concepts of tensor algebra, such as addition, multiplication by scalars, and tensor products, are based on linear operations that are independent of the space's curvature, making them valid in both Euclidean and non-Euclidean manifolds.

  • How are the permutation symbols related to the concepts of determinants and relative tensors?

    -Permutation symbols are used in the calculation of determinants and are themselves relative tensors with specific weights. They are invariant expressions when the indexes are mixed and have weights of one or negative one depending on the position of the indexes.

  • What is the role of the volume element in tensor calculus?

    -The volume element, which is the absolute value of the Jacobian, is a weighted relationship that connects the volume elements in different coordinate systems, and it is essential for understanding transformations involving volume changes.

  • How are the concepts of raising and lowering indices applied in tensor calculus?

    -Raising and lowering indices involve using the metric tensors to move an index from the upper position to the lower position (raising) or vice versa (lowering). This process is crucial for tensor manipulation and is applicable in both Euclidean and non-Euclidean spaces.

  • What is the significance of the dot product in the context of this video?

    -The dot product is significant as it is used to calculate the scalar product of vectors in the tangent plane. The concept of the dot product is applicable to all manifolds, including those that are curved.

  • What is the purpose of reviewing these concepts in the context of non-Euclidean manifolds?

    -The purpose of reviewing these concepts is to establish a solid baseline and to show that most of the tensor calculus operations developed for Euclidean spaces can be extended to non-Euclidean manifolds without modification.

Outlines
00:00
📚 Universality of Tensor Calculus Concepts

This paragraph reviews previous results in tensor calculus, emphasizing their universal applicability to all manifolds, including both Euclidean and non-Euclidean spaces. The narrator explains that the foundational concepts, such as covariant basis vectors derived from partial derivatives of the position vector, are not limited to Euclidean spaces. The paragraph serves as a baseline for further exploration of manifold-specific topics. Key references to previous videos are provided for deeper understanding, highlighting the consistency of derivations across different types of spaces.

05:01
🔍 Detailed Exploration of Tangent Plane Vectors and Tensors

The second paragraph delves deeper into the specifics of working with vectors in the tangent plane of a manifold. It discusses the covariant and contravariant basis vectors, their properties, and how they relate to each other through the metric tensors. The paragraph also covers tensor algebra, including the operations of addition, multiplication by scalars, and tensor products. The concept of raising and lowering indices using metric tensors is explained, along with the implications for tensor transformations. The summary underscores the applicability of these tensor properties to any manifold, regardless of its curvature.

10:03
📘 Extending Tensor Calculus to Include Determinants and Advanced Concepts

The final paragraph extends the discussion to include determinants, permutation symbols, and advanced tensor concepts such as relative tensors, cofactors, volume elements, and the Levi-Civita symbols. It confirms that most of these topics hold true for curved spaces as well, with adjustments made for the dimensionality of the space. The paragraph concludes by setting the stage for the introduction of new concepts unique to submanifolds, such as the shift tensor, which will be explored in subsequent videos.

Mindmap
Keywords
💡Manifolds
Manifolds are a fundamental concept in the video, referring to a space that is locally similar to Euclidean space but may have a different global structure. The video discusses that most of the results from previous videos are universally applicable to all manifolds, whether they are Euclidean or non-Euclidean. This establishes a baseline for exploring more specific topics related to non-Euclidean manifolds.
💡Covariant Basis Vectors
Covariant basis vectors are derived from the partial derivative of a position vector and are used to establish a local coordinate system on a manifold. In the video, the script mentions using the technique from a previous video to derive these vectors, which are essential for understanding how to work with vectors tangent to the surface of a manifold.
💡Tangent Plane
The tangent plane is a concept that is central to the discussion of vectors on manifolds. It is the plane that touches the manifold at a given point, and all vectors considered in the video are restricted to this plane. The script emphasizes that linear combinations of basis vectors and other vector operations are relative to vectors within the tangent plane.
💡Jacobian
The Jacobian matrix is a key concept in tensor calculus, representing the transformation between different coordinate systems. In the script, the Jacobian is defined as the partial derivative of one set of coordinates with respect to another, which is crucial for understanding covariant and contravariant transformations on manifolds.
💡Covariant and Contravariant Transformations
These transformations relate to how indices are handled when changing coordinate systems. A covariant transformation has the free index at the bottom, while a contravariant transformation has it at the top. The video script explains that these concepts are essential for understanding how tensors transform between different coordinate systems on a manifold.
💡Metric Tensor
The metric tensor is a fundamental object in differential geometry, describing the geometry of a space through the dot product of basis vectors. The script discusses both covariant and contravariant metric tensors, which are used to define distances and angles on the manifold, and are crucial for understanding the intrinsic geometry of curved spaces.
💡Tensor Algebra
Tensor algebra encompasses the rules and operations for manipulating tensors, such as addition, multiplication by scalars, and contraction. The video script notes that all properties of tensor algebra derived in previous videos continue to be valid in the context of manifolds, whether Euclidean or curved.
💡Raising and Lowering Indices
Raising and lowering indices is a process in tensor calculus that involves using metric tensors to change the position of an index from a contravariant to a covariant position (raising) or vice versa (lowering). The script explains that this process is valid for tensors on manifolds and is essential for working with tensor equations.
💡Dot Product
The dot product is a binary operation that measures the extent to which two vectors are in the same direction. In the context of the video, the dot product is discussed in relation to vectors in the tangent plane of a manifold, which is crucial for understanding how to compute scalar quantities from vector fields on the manifold.
💡Permutation Symbols
Permutation symbols, also known as Levi-Civita symbols, are used in various mathematical contexts, including tensor calculus, to represent the sign of a permutation. The video script mentions that permutation symbols are applicable to all manifolds and are used in the calculation of determinants and other related concepts.
💡Determinants
Determinants are a way to find the volume scaling factor of a linear transformation. In the script, determinants are discussed in the context of manifolds, where they are used to understand how volumes change under coordinate transformations, which is important for understanding the overall structure of the manifold.
💡Volume Element
A volume element is a measure of the size of a small region in a manifold. The script explains that the volume element is related to the absolute value of the Jacobian determinant, which is crucial for understanding how to integrate over manifolds and compute volumes in curved spaces.
💡Levi-Civita Symbols
Levi-Civita symbols are a generalization of the permutation symbols and are used in the context of integration over manifolds. The video script discusses how these symbols, combined with the volume element, are used to define integrals over curved spaces, which is essential for understanding advanced concepts in differential geometry.
Highlights

The video revisits prior results in tensor calculus to establish their universal applicability to all manifolds, including non-Euclidean ones.

Syntax has been restructured to reflect surface coordinates in two dimensions, applicable to both Euclidean space and curved surfaces.

Reference numbers are provided for viewers to revisit the derivation of initial concepts for a deeper understanding.

Covariant basis vectors can be derived using partial derivatives of the position vector, a technique applicable to both flat and curved surfaces.

Linear combinations of basis vectors with vector components are possible, all relative to vectors in the tangent plane.

Transformations between coordinate systems are discussed, introducing the concept of covariant and contravariant transformations.

The Jacobian, defined as the partial derivative of one set of coordinates with respect to another, is crucial for understanding transformations.

The inverse of the Jacobian and its contraction with the original to form a Kronecker delta are explained.

Covariant metric tensors are introduced as combinations of dot products between covariant basis vectors, with symmetric indexes.

The contravariant metric tensor is defined as the inverse of the covariant metric tensor, allowing for the definition of contravariant basis vectors.

The properties of contravariant and covariant basis vectors in the tangent plane are discussed, ensuring they lie within the plane.

Tensor algebra properties, including addition, multiplication by scalars, and linear operations, are highlighted as universally applicable.

Tensor products and contractions are shown to be valid operations in both Euclidean and non-Euclidean spaces.

The concept of raising and lowering indices using metric tensors is discussed, with syntax using dots for placeholders.

The dot product of vectors in the tangent plane is shown to be a valid concept, extending to curved surfaces.

The applicability of all concepts from the first 26 videos of the series to all manifolds is emphasized.

Permutation symbols and their properties, including their role as relative tensors, are discussed in the context of determinants.

Cofactors and their relationship to the inverse of the determinant are explained, applicable in two-dimensional and non-Euclidean forms.

The volume element and its relationship to the absolute value of the Jacobian are highlighted, showing its weighted nature.

Levi-Civita symbols are defined using permutation symbols and volume elements, maintaining their validity in all manifolds.

Transcripts

Browse More Related Video

Video 68 - Christoffel Symbol for Surfaces - Part 1

Video 73 - Surface Covariant Derivative Properties

Tensor Calculus 4b: Position Vector, Covariant Basis, Covariant Metric Tensor, Contravariant Basis

Video 57 - Embedded Manifolds

Video 62 - Embedded Curve

Video 22 - Raising & Lowering Indexes

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Tensor CalculusManifoldsCovariantContravariantMetric TensorJacobianTransformationEuclidean SpaceNon-EuclideanMathematicsEducational