Tensor Calculus 26 - Ricci Tensor/Scalar Properties

eigenchris

28 Oct 201928:58

EducationalLearning

32 Likes 10 Comments

TLDRThis video delves into the properties of the Ricci tensor and scalar, integral to understanding Einstein's field equations in general relativity. It covers contractions of the Riemann tensor, the symmetry of the Ricci tensor, the second and contracted Bianchi identities, and introduces the Einstein tensor. The script concludes with a discussion on how these concepts relate to the curvature of space-time and the existence of phenomena like black holes and cosmic expansion.

Takeaways

📚 The video discusses properties of the Ricci tensor and scalar, building on previous videos about the Riemann tensor and its geometric meanings.
🔍 It covers five main properties: contractions of the Riemann tensor leading to the Ricci tensor, symmetry of the Ricci tensor, the second Bianchi identity, the contracted Bianchi identity, and the Einstein tensor.
🔄 The Ricci tensor is derived from the Riemann tensor through specific contractions, with only one meaningful contraction, highlighting its significance in tensor calculus.
🔱 The Ricci tensor is symmetric, meaning R_ab equals R_ba, which is a fundamental property in the study of curvature in space-time.
🌀 The second Bianchi identity is a property of the Riemann tensor that is crucial for deriving properties of the Ricci tensor, involving the covariant derivative.
📉 The contracted Bianchi identity shows that a certain combination of the Ricci tensor, when covariantly differentiated and with matching indices, results in zero.
🌐 The Einstein tensor is introduced as a modified version of the Ricci tensor, which has a zero covariant derivative when the indices match, symbolized by G.
🌌 Einstein's field equations are mentioned, which relate the energy-momentum tensor to the curvature of space-time, represented by the Einstein tensor.
🔗 The video connects the mathematical concepts to physical phenomena like black holes and the expansion of the universe, providing a bridge between theory and observation.
📈 The script emphasizes the importance of understanding tensor calculus for grasping the geometric foundation of general relativity and its predictions.
🚀 The series on tensor calculus concludes with this video, with plans for a follow-up series on general relativity to delve deeper into these concepts.

Q & A

What are the main topics covered in the video?
-The video discusses the properties of the Ricci tensor and Ricci scalar, including contractions of the Riemann tensor, symmetry of the Ricci tensor, the second Bianchi identity, the contracted Bianchi identity, the Einstein tensor, and the Einstein field equations of general relativity.
What is the Ricci tensor and how is it derived from the Riemann tensor?
-The Ricci tensor is a rank-2 symmetric tensor that is derived from the Riemann tensor by performing a contraction over the upper index and the middle lower index of the Riemann tensor components.
What does the symmetry of the Ricci tensor imply?
-The symmetry of the Ricci tensor implies that the tensor is invariant under the exchange of its indices, meaning R_{ij} = R_{ji}. This reflects the fact that the Ricci tensor, when viewed as a matrix, has a lower triangle that is a mirror image of the upper triangle.
Can you explain the second Bianchi identity?
-The second Bianchi identity is a property of the Riemann tensor that states the sum of the Riemann tensor components with the first upper and lower indices being the same and the last three indices cyclically permuted equals zero. It is also expressed as the covariant derivative of the Riemann tensor being zero when the first and second indices are swapped.
What is the contracted Bianchi identity and what does it imply?
-The contracted Bianchi identity is a result derived from the second Bianchi identity, where the covariant derivative of a modified Ricci tensor, which includes the Ricci scalar and the metric tensor, equals zero when the derivative index matches one of the tensor indices. This identity is important for understanding the conservation laws in general relativity.
What is the Einstein tensor and how does it relate to the Ricci tensor?
-The Einstein tensor is a rank-2 tensor that is derived from the Ricci tensor by subtracting half of the metric tensor multiplied by the Ricci scalar. It has the property that its covariant derivative is zero when the indices match, making it a key component in the Einstein field equations.
What are the Einstein field equations and what do they represent?
-The Einstein field equations are the fundamental equations of general relativity that describe the curvature of spacetime due to the presence of mass and energy. They equate the Einstein tensor, which represents spacetime curvature, to the energy-momentum tensor, which represents the distribution and flow of matter and energy.
How many unique equations are there in the Einstein field equations?
-There are ten unique equations in the Einstein field equations due to the symmetry of the Ricci tensor, metric tensor, and energy-momentum tensor, which reduces the 16 potential equations to 10 independent ones.
What is the cosmological constant and its role in the Einstein field equations?
-The cosmological constant, denoted by Lambda (λ), is a term in the Einstein field equations that represents a possible form of dark energy. It accounts for the observed expansion of the universe and is related to the curvature of spacetime on the largest scales.
What is the significance of the Ricci scalar in the context of the Einstein field equations?
-The Ricci scalar is a single number that is derived from the Ricci tensor by contracting its indices. It is a measure of the curvature of spacetime and plays a crucial role in the Einstein field equations, where it contributes to the overall curvature that influences the motion of matter and energy.
How does the video script connect the properties of the Ricci tensor to the broader concepts of general relativity?
-The script connects the properties of the Ricci tensor to general relativity by showing how these properties, such as symmetry and the Bianchi identities, lead to the definition of the Einstein tensor and are ultimately incorporated into the Einstein field equations, which describe the fundamental relationship between matter, energy, and spacetime curvature.

Outlines

00:00

📚 Introduction to Ricci Tensor Properties

The speaker introduces the topic of the Ricci tensor and its properties, setting the stage for a detailed exploration. They recommend watching previous videos for better understanding and outline five key properties to be discussed: contractions of the Riemann tensor leading to the Ricci tensor, the symmetry of the Ricci tensor, the second Bianchi identity, the contracted Bianchi identity, and the Einstein tensor's role in Einstein's field equations. The summary also includes a brief review of the Riemann tensor and its properties, setting a foundation for the upcoming discussion.

05:00

🔍 Symmetry of the Ricci Tensor and Contractions

This paragraph delves into proving the symmetry of the Ricci tensor, which is a crucial property for understanding its behavior as a matrix in space-time geometry. The proof utilizes the first Bianchi identity of the Riemann tensor and demonstrates that the Ricci tensor remains unchanged when its indices are swapped. Additionally, the paragraph explores the different possible contractions of the Riemann tensor, showing that only the Ricci tensor itself is of interest, as other contractions either result in zero or are equivalent to the Ricci tensor with a sign change.

10:02

📘 Second Bianchi Identity and Covariant Derivatives

The speaker explains the second Bianchi identity, a property of the Riemann tensor that is instrumental in deriving further properties of the Ricci tensor. They provide a detailed proof using component notation and introduce the concept of covariant derivatives of the Riemann tensor. The paragraph also discusses the use of normal coordinates to simplify the proof and touches upon the semicolon notation for covariant derivatives, which is essential for understanding the manipulation of tensors in the context of curvature.

15:02

🔧 Contracted Bianchi Identity and Einstein Tensor

This section presents the contracted Bianchi identity, which relates to the covariant derivative of the Ricci tensor. The proof involves a summation with the inverse metric tensor and leverages the second Bianchi identity. The paragraph also introduces the Einstein tensor, a modified version of the Ricci tensor that has a zero covariant derivative when certain indices match. This property is fundamental to the formulation of the Einstein field equations in general relativity.

20:05

🌌 Einstein Field Equations and Space-Time Curvature

The speaker connects the properties of the Ricci tensor to the Einstein field equations of general relativity. They discuss the energy-momentum tensor and its relation to the curvature of space-time, introducing the concept that energy and momentum are equivalent to space-time curvature. The paragraph outlines the Einstein field equations, which include the Einstein tensor, and explains the presence of the cosmological constant, which is associated with the expansion of the universe and the concept of dark energy.

25:07

🔚 Summary of Ricci Tensor Properties and Future Topics

In conclusion, the speaker summarizes the key properties of the Ricci tensor discussed throughout the video, emphasizing its importance in the context of general relativity. They recap the main points: the contractions leading to the Ricci tensor, its symmetry, the second and contracted Bianchi identities, and the Einstein tensor. The speaker also hints at upcoming videos that will explore general relativity in more depth, including the mathematical explanations for phenomena like the bending of light by black holes and the expansion of the universe.

Mindmap

Keywords

💡Ricci Tensor

The Ricci tensor is a key concept in differential geometry and general relativity, representing the amount by which the geometry of a curved spacetime deviates from being flat. In the video, the Ricci tensor is discussed in the context of its properties and its role in the Einstein field equations, which describe the fundamental interaction of gravitation as the curvature of spacetime caused by mass and energy.

💡Ricci Scalar

The Ricci scalar, derived from the Ricci tensor, is a single number that characterizes the curvature of a given spacetime. It is obtained by contracting the Ricci tensor with the metric tensor. The video explains how the Ricci scalar is used in the Einstein field equations, indicating the density of curvature, which is a measure of the overall 'curvature' of spacetime at a point.

💡Riemann Tensor

The Riemann curvature tensor is a central object in the study of curvature in the context of Riemannian and pseudo-Riemannian geometry. It generalizes the concept of Gaussian curvature in two dimensions to higher dimensions. In the script, the Riemann tensor is mentioned as the starting point for deriving the Ricci tensor and scalar, highlighting its importance in understanding the properties of spacetime curvature.

💡Bianchi Identity

The Bianchi identities are fundamental properties of the Riemann tensor that relate to its covariant derivatives. The video discusses the second Bianchi identity, which states that the covariant derivative of the Riemann tensor, when certain indices are cycled, sums to zero. This identity is crucial in proving other properties of the Ricci tensor and is used in the derivation of the Einstein tensor.

💡Einstein Tensor

The Einstein tensor, denoted by G, is a modification of the Ricci tensor that includes a term involving the Ricci scalar and the metric tensor. It is introduced in the video as having a zero covariant derivative when certain indices match, which is a necessary condition for the Einstein field equations. The Einstein tensor embodies the relationship between the curvature of spacetime and the distribution of matter and energy.

💡Einstein Field Equations

The Einstein field equations are the core equations of general relativity, which describe how mass and energy distribution cause spacetime to curve, and how this curvature influences the motion of particles. The video mentions these equations in the context of the Einstein tensor and the relationship between energy-momentum and spacetime curvature, which is central to understanding phenomena like black holes and the expansion of the universe.

💡Covariant Derivative

The covariant derivative is a generalization of the directional derivative to curved spaces, such as those described by general relativity. It is used in the video to discuss the properties of tensors like the Riemann and Ricci tensors, and to derive the Bianchi identities. The covariant derivative is essential for understanding how tensors change from point to point in spacetime.

💡Metric Tensor

The metric tensor is a fundamental concept in differential geometry, defining the notion of distance and angle in a curved space. In the context of the video, the metric tensor is used in the construction of the Ricci scalar and in the definition of the Einstein tensor. It is also central to the concept of metric compatibility, which allows for the manipulation of indices in tensors with covariant derivatives.

💡Symmetric Tensor

A symmetric tensor is one where the components remain unchanged when the indices are swapped. The Ricci tensor is shown to be symmetric in the video, which is an important property because it reduces the number of independent components and simplifies the mathematical formulation of the Einstein field equations.

💡Connection Coefficients

Connection coefficients, also known as Christoffel symbols, are used in the definition of the covariant derivative and the curvature tensors. They encode the 'shape' of the space in which we are taking derivatives. In the video, connection coefficients are mentioned in the context of calculating the Riemann tensor components and are integral to the discussion of the properties of spacetime curvature.

💡General Relativity

General relativity is the theory of gravitation proposed by Albert Einstein, which describes gravity not as a force but as a curvature of spacetime caused by mass and energy. The video concludes with a brief mention of the upcoming series on general relativity, where these concepts, including the Einstein field equations and the properties of the Ricci tensor, will be further explored in the context of explaining phenomena like the bending of light and the expansion of the universe.

Highlights

Introduction to properties of the Ricci tensor and scalar, with prerequisites from previous videos on the Riemann tensor.

Explanation of the different contractions of the Riemann tensor and their relation to the Ricci tensor.

Demonstration of the Ricci tensor's symmetry, a key property in its mathematical formulation.

Proof of the second Bianchi identity using both component form and normal coordinates.

Introduction of the contracted Bianchi identity and its implications for the Ricci tensor.

Definition and role of the Einstein tensor in the context of general relativity.

Discussion on the appearance of the Ricci tensor and scalar in Einstein's field equations.

Review of the Riemann curvature tensor and its properties, setting the stage for further exploration.

Detailed exploration of the contractions of the Riemann tensor, highlighting the uniqueness of the Ricci tensor.

In-depth proof of the Ricci tensor's symmetry using the first Bianchi identity of the Riemann tensor.

Explanation of the covariant derivative and its notation, crucial for understanding tensor operations.

Simplification of the second Bianchi identity proof using Riemann normal coordinates.

Abstract proof of the second Bianchi identity applicable in all coordinate systems.

Derivation of the contracted Bianchi identity from the second Bianchi identity.

Introduction of the Einstein tensor as a modified version of the Ricci tensor with a zero covariant derivative.

Overview of Einstein's field equations and their significance in general relativity.

Summary of the tensor calculus series and预告 of the upcoming general relativity series.

Transcripts

Browse More Related Video

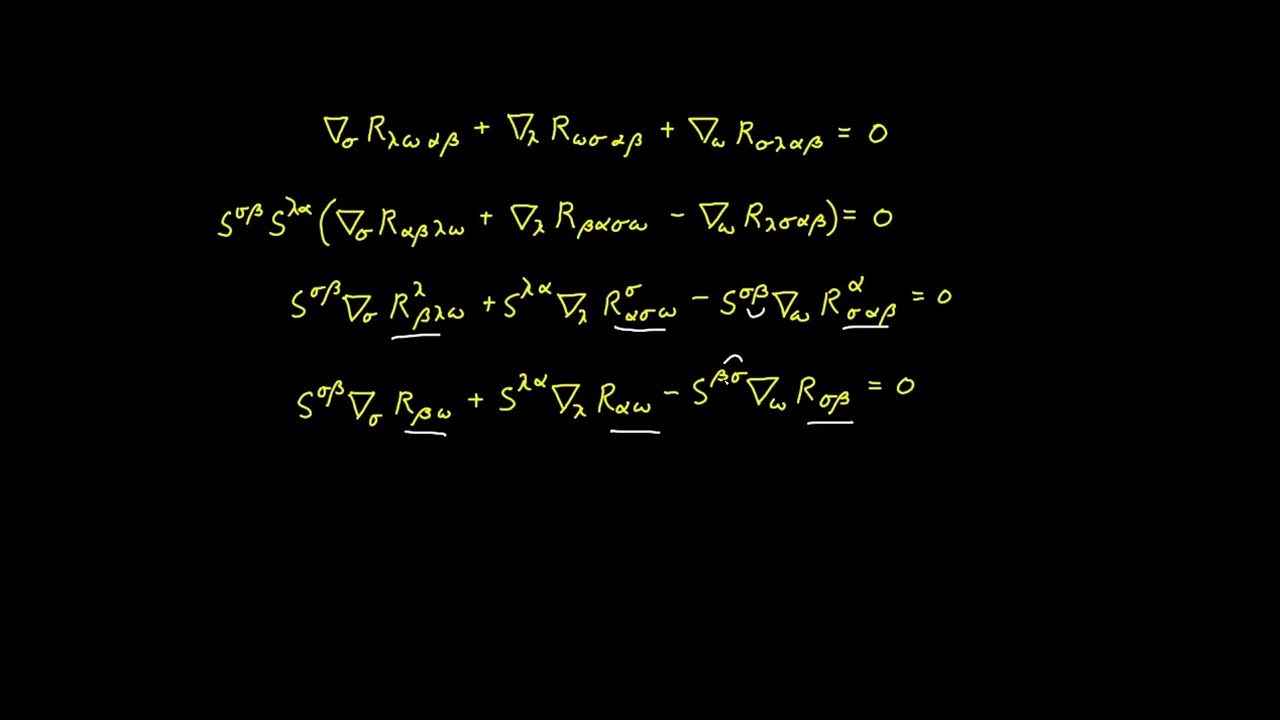
Video 87 - Ricci & Einstein Tensors

Tensor Calculus 24: Ricci Tensor Geometric Meaning (Sectional Curvature)

Einstein Field Equations - for beginners!

Tensor Calculus 23: Riemann Curvature Tensor Components and Symmetries

General Relativity Lecture 9

Einstein's Field Equations of General Relativity Explained

Related Tags

Ricci Tensor Ricci Scalar General Relativity Space-Time Curvature Einstein Tensor Bianchi Identity Tensor Calculus Einstein Equations Cosmological Constant