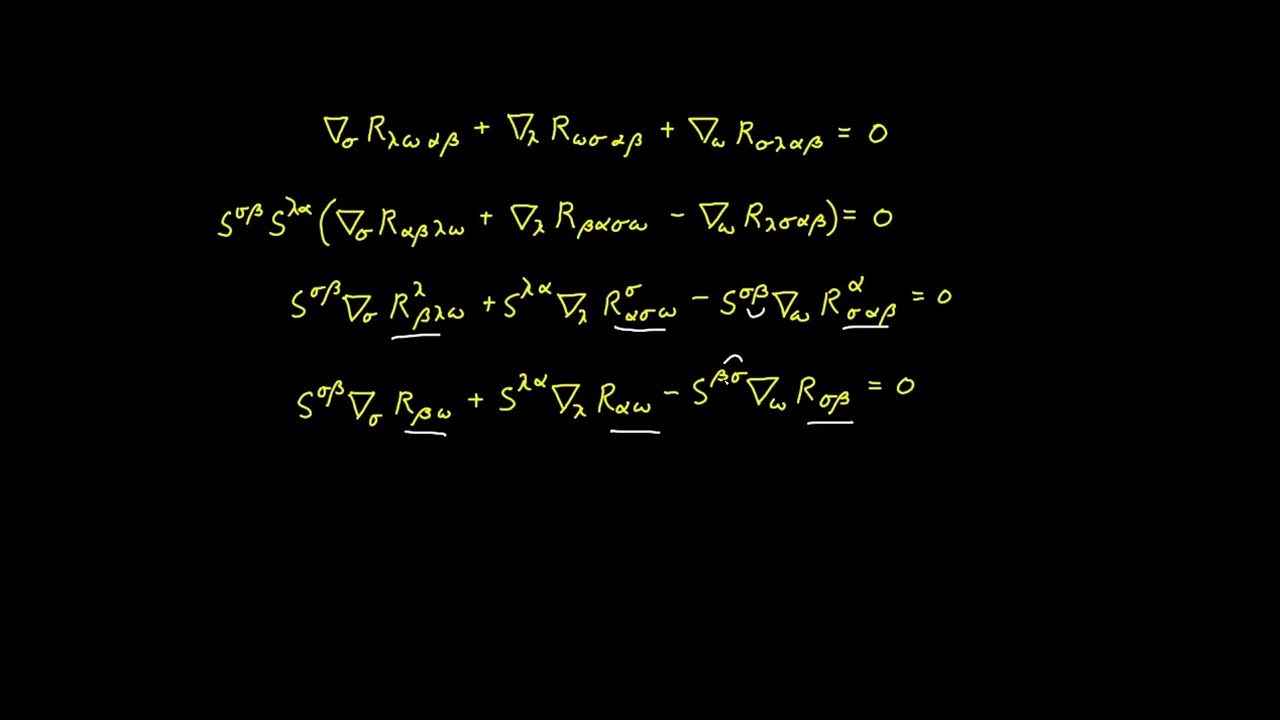Tensor Calculus 24: Ricci Tensor Geometric Meaning (Sectional Curvature)
TLDRThis video script delves into the geometrical significance of the Ricci curvature tensor and scalar, derived from the Riemann curvature tensor. It aims to provide a visual intuition for the Ricci tensor, which measures volume changes along geodesics, and explains how these concepts are central to understanding gravity in the context of general relativity. The script also covers the Ricci scalar's role in comparing volumes in curved versus flat spaces, using the sphere as an example to illustrate positive Ricci curvature. The explanation is enriched with mathematical details and visual examples, promising a deeper understanding of these fundamental concepts in differential geometry.
Takeaways
- 📚 The video discusses the geometrical meaning of the Ricci curvature tensor and the Ricci scalar, both derived from the Riemann curvature tensor.
- 🔍 The Ricci tensor measures how volumes grow or shrink as they move along geodesics, which is visualized through two geometrical approaches: sectional curvature and the volume element derivative.
- 🌐 The Ricci scalar compares the volume of a ball in curved space to that in flat space, indicating deviations from the standard volume.
- 📈 The Ricci tensor represents gravity in general relativity, as it shows how space-time curvature affects the convergence or divergence of geodesics.
- 👥 An example given is two people walking on the moon's surface along geodesics, naturally getting closer due to the moon's curvature, illustrating volume change represented by the Ricci tensor.
- 🧠 The Einstein field equations relate the Ricci tensor to gravitational attraction, where more curvature leads to quicker convergence of bodies.
- 📏 The Ricci scalar quantifies the amount of additional space that can fit inside a circle in curved space compared to flat space, a concept used in science fiction for 'bigger on the inside' scenarios.
- 📉 The video explains the concept of geodesic deviation and its relation to the Riemann tensor, which is crucial for understanding how geodesics move relative to one another in curved spaces.
- 📐 Sectional curvature is defined as a normalized measure of geodesic convergence or divergence within a specific plane, independent of the choice of vectors within that plane.
- 🔢 The Ricci curvature is an average of all possible sectional curvatures containing a given direction vector, indicating overall volume change in that direction.
- 🌍 A specific example of the sphere is used to illustrate positive Ricci curvature, where geodesics always converge, consistent with the intuitive understanding of a spherical surface.
Q & A
What are the main topics discussed in the video script?
-The video script discusses the geometrical meaning of the Ricci curvature tensor, the Ricci scalar, and their derivation from the Riemann curvature tensor. It also explains how these concepts relate to the visualization of space-time curvature and the Einstein field equations in general relativity.
What is the Ricci tensor and how does it relate to volume changes along geodesics?
-The Ricci tensor is a measure of how volumes grow or shrink as they move along geodesics. It tracks volume changes and can be thought of as summarizing the Riemann tensor, providing information about the curvature of space-time and its effect on volumes.
Can you explain the Ricci scalar in the context of the video script?
-The Ricci scalar is a single number that quantifies the amount by which the volume of a ball in curved space deviates from the volume of a ball of the same radius in flat space. It is used to compare volumes and is related to the overall curvature of the space.
What is the significance of geodesic deviation in understanding the Ricci tensor?
-Geodesic deviation is the second derivative of a separation vector between two geodesics. It is significant in understanding the Ricci tensor because it reveals how geodesics move relative to one another, indicating whether they are converging or diverging due to the curvature of space.
How does the video script connect the Ricci tensor to the concept of gravity in general relativity?
-The video script connects the Ricci tensor to gravity by explaining that the Ricci tensor represents how quickly bodies get drawn together in curved space-time. In general relativity, gravitational attraction is the natural result of this curvature, without the need for forces as in Newtonian gravity.
What is the difference between sectional curvature and Ricci curvature as explained in the script?
-Sectional curvature is a measure of how geodesics converge or diverge within a specific plane, while Ricci curvature is an average of all possible sectional curvatures containing a given direction vector. It provides a measure of volume change in that direction.
How does the Ricci tensor act on a vector to give the Ricci curvature?
-The Ricci tensor acts on a vector twice, once for each index, to yield the Ricci curvature. This curvature is obtained by summing over the components of the Ricci tensor with the vector serving as the direction of interest.
What is the geometrical interpretation of positive, negative, and zero Ricci curvature?
-Positive Ricci curvature indicates that geodesics are converging, leading to a decrease in volume. Negative Ricci curvature means geodesics are diverging, causing an increase in volume. Zero Ricci curvature implies that the volume does not change as geodesics move, although the shape may still be altered.
Can you provide an example of how the Ricci curvature is calculated for a sphere, as mentioned in the script?
-For a sphere, the Ricci curvature is positive everywhere. This is because there is only one independent nonzero component of the Riemann tensor, and the metric tensor for the sphere allows for the Ricci tensor components to be determined, resulting in a positive curvature that signifies geodesics will always converge.
What is the significance of the Ricci scalar in the context of science fiction concepts like the TARDIS from Doctor Who?
-The Ricci scalar is used to explain how spaces can be 'bigger on the inside' than their external boundaries suggest, as seen in the TARDIS from Doctor Who. This is a result of the properties of curved space, where more volume can be contained within a given boundary due to the curvature.
Outlines
📚 Introduction to Ricci Tensor and Scalar
This paragraph introduces the video's focus on the geometrical meaning of the Ricci tensor and scalar, derived from the Riemann curvature tensor. The speaker aims to provide a visual intuition for the Ricci tensor, which measures volume changes along geodesics, using the example of a rabbit on a 2D surface of the Moon. The Ricci scalar is explained as a measure comparing volumes in curved versus flat spaces. The Einstein field equations are mentioned to relate the Ricci tensor to gravity in general relativity, suggesting that gravitational attraction is a result of space-time curvature rather than a force. The paragraph sets the stage for a deeper dive into the mathematical properties of the Ricci tensor in a subsequent video.
🔍 Geodesic Deviation and Sectional Curvature
The second paragraph delves into the concept of geodesic deviation, explaining how it is calculated using the Riemann tensor and the implications it has for understanding how geodesics move relative to one another. The discussion covers the sign convention used in the formula and its importance in determining whether geodesics are converging or diverging. The sectional curvature is introduced as a normalized measure that depends on the choice of plane rather than the specific vectors, allowing for a consistent way to assess the behavior of geodesics within that plane.
📐 Mathematical Exploration of Ricci Curvature
This paragraph continues the mathematical exploration by discussing the Ricci curvature, which is derived from the sectional curvatures of all possible planes containing a given direction vector. The Ricci curvature is visualized through various examples, illustrating scenarios where geodesics are either converging, diverging, or remaining constant, each resulting in positive, negative, or zero Ricci curvature, respectively. The paragraph emphasizes that Ricci curvature informs about volume changes rather than shape changes, highlighting its significance in understanding the behavior of volumes in curved spaces.
🌐 Ricci Tensor and Curvature in Different Geodesic Scenarios
The fourth paragraph provides a deeper understanding of the Ricci tensor and curvature through visual examples. It explains how in scenarios with straight geodesics, the Ricci curvature is zero, indicating no volume change. Conversely, when geodesics converge or diverge, the Ricci curvature is positive or negative, respectively, leading to volume shrinkage or expansion. The paragraph also presents a case where geodesics exhibit both convergence and divergence, resulting in a net Ricci curvature of zero and no change in volume, despite changes in shape.
📘 Ricci Tensor Components and Transformation Properties
The fifth paragraph focuses on the components of the Ricci tensor, which are derived from the Riemann tensor through a process of summation and contraction. It explains how the Ricci tensor, when acting on a vector twice, yields the Ricci curvature. The paragraph also discusses the transformation properties of the Ricci curvature under a change of orthonormal basis, demonstrating that the Ricci curvature is invariant under such transformations, thus its value is consistent regardless of the chosen basis.
🌕 Ricci Curvature of a Sphere and Upcoming Volume Element Discussion
In the final paragraph, the speaker provides a specific example of Ricci curvature calculation for a sphere, showing that it results in positive curvature, indicative of converging geodesics. This aligns with the earlier Moon example and reinforces the concept that positive Ricci curvature leads to volume reduction. The paragraph concludes by预告ing a continuation of the discussion on the Ricci tensor and scalar in relation to volume elements in a subsequent video, inviting viewers to stay tuned for further insights.
Mindmap
Keywords
💡Ricci Curvature Tensor
💡Ricci Scalar
💡Riemann Curvature Tensor
💡Geodesic
💡Geodesic Deviation
💡Sectional Curvature
💡Volume Element
💡Einstein Field Equations
💡Orthonormal Basis
💡Differential Geometry
Highlights
The video discusses the geometrical meaning of the Ricci curvature tensor and the Ricci scalar derived from the Riemann curvature tensor.
The Ricci tensor tracks volume changes along geodesics, indicating how volumes grow or shrink as they move along these paths.
Two geometrical approaches to understanding the Ricci tensor are introduced: sectional curvature and the volume element derivative.
The Ricci scalar is used to compare the volume of a ball in curved space to that in flat space, indicating space's deviation from flat geometry.
The Einstein field equations relate the Ricci tensor to gravity in general relativity, where curvature equates to gravitational attraction.
Visualizations of the Ricci tensor on a 2D surface, like the moon, demonstrate how geodesics converge and volumes shrink.
The Ricci scalar quantifies the additional space that can fit inside a circle in curved space compared to flat space.
The concept of geodesic deviation is explored, explaining how geodesics move relative to one another in curved spaces.
Sectional curvature is defined as a measure of how geodesics converge or diverge within a specific plane.
The Ricci curvature is presented as an average of all possible sectional curvatures containing a given vector.
Examples illustrate the visualization of Ricci curvature in different scenarios, such as when geodesics are straight, converging, or diverging.
The video explains the mathematical relationship between the Ricci tensor and the Ricci curvature.
The transformation properties of the Ricci tensor and curvature under a change of basis are discussed.
A specific example of Ricci curvature on a spherical surface is provided, demonstrating positive curvature and converging geodesics.
The video distinguishes between the Ricci tensor's role in volume change and shape change, emphasizing its impact on volume.
The upcoming continuation of the video series is teased, promising further exploration of the Ricci tensor and scalar.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: