Einstein's Field Equations of General Relativity Explained
TLDRThis script delves into Einstein's Field Equations, which illustrate how mass and momentum warp space-time, creating gravity and phenomena like gravitational waves and black holes. It explains the concept of space-time curvature, the use of basis vectors, and parallel transport to understand motion in a curved space-time. The script further explores the mathematical framework, including tensors and the metric tensor, to describe space-time intervals and curvature. It also touches on the cosmological constant related to dark energy and the stress-energy-momentum tensor, which details the energy and momentum distribution in space-time. The video concludes by emphasizing that General Relativity does not necessitate embedding space-time in higher dimensions, highlighting the non-Euclidean nature of our universe.
Takeaways
- 🌌 Einstein's Field Equations are the fundamental equations of general relativity that describe how mass and momentum create a curvature in space-time, leading to the phenomenon of gravity.
- 🌪️ These equations also account for other cosmic phenomena such as gravitational waves, black holes, and the accelerating expansion of the Universe.
- 📐 The concept of space-time involves four dimensions, three spatial and one temporal, and can appear flat when observing a very small section, similar to how the Earth appears flat from a limited perspective.
- 🔍 By approximating regions of space-time as flat and using mathematical axes for spatial dimensions and time, different observers can have different orientations due to Special Relativity.
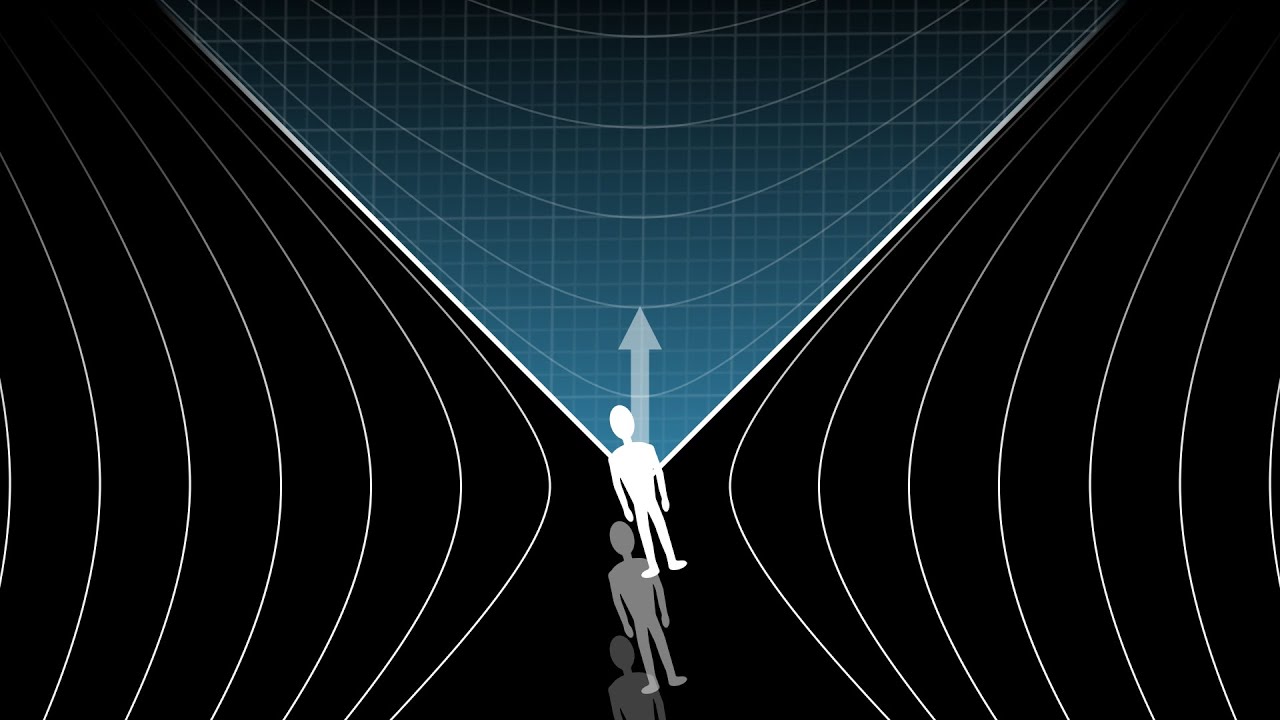
- 🚀 The path of an object through curved space-time can be determined by repeatedly correcting for the curvature and moving in the direction of a 'time arrow', creating the illusion of a gravitational force.
- 📊 To describe four-dimensional space-time, four coordinates (X0, X1, X2, X3) are used, with index values indicating different dimensions and not exponents.
- 🔄 The basis vectors and their rates of change, represented by symbols with three index values, are crucial for understanding how coordinates change in both flat and curved space-time.
- 🔗 Newtonian physics can be a good approximation for situations where Einstein's Field Equations predict small deviations, with gravitational acceleration related to the curvature of space-time.
- 🔄 The process of parallel transport allows a vector to move through space-time while accounting for curvature, which can result in a change in direction upon returning to the starting point.
- 📉 Curvature of space-time can be defined by the change in angle of a vector as it travels around an area and returns to its original position, with positive and negative curvatures indicating different rotational directions.
- 🔢 Einstein's Field Equations involve tensors that represent different numbers at each point in space-time, and these values are dependent on the chosen coordinate system.
- 🌌 The cosmological constant in the equations governs the acceleration of the Universe's expansion, associated with dark energy, and the stress-energy-momentum tensor describes the density of energy and momentum at each point in space-time.
Q & A
What do Einstein's Field Equations describe?
-Einstein's Field Equations describe how mass and momentum create a curvature in space-time, which results in the apparent force of gravity. They also describe phenomena such as gravitational waves, black holes, and the accelerating expansion of the Universe.
Why does space-time appear flat when we zoom in on a small section?
-Space-time appears flat when we zoom in on a small section because, similar to how the Earth appears flat when we look at a tiny portion of it, the curvature of space-time is not noticeable at a small scale.
What is the significance of the red arrow in the script?
-The red arrow represents the direction of movement along the time axis as seen by an observer. It is used to illustrate the process of correcting for the approximation of flat space-time as one moves forward in time.
What are basis vectors and how are they related to space-time?
-Basis vectors are directional arrows that show the change in position when one of the coordinates is incremented at various points in space. They are related to space-time as they help define the rate at which the basis vectors change due to the curvature of space-time or the use of a curved coordinate system in a flat space-time.
How does the concept of parallel transport relate to understanding space-time curvature?
-Parallel transport is the process of moving a vector over long distances in space-time while taking the curvature into account. It helps in understanding space-time curvature by showing how much a vector changes direction when it is moved around a closed path in curved space-time.
What is the role of the cosmological constant in Einstein's Field Equations?
-The cosmological constant in Einstein's Field Equations governs the rate at which the expansion of the Universe is accelerating, which is associated with the phenomenon of dark energy.
How does the stress-energy-momentum tensor contribute to Einstein's Field Equations?
-The stress-energy-momentum tensor describes the density of energy and momentum at each point in space-time, including the contributions from matter and electromagnetic radiation. It is a key component on the right side of Einstein's Field Equations.
What is the difference between the curvature scalar 'R' and the tensor variable with 'R' and two index values?
-The curvature scalar 'R' signifies the curvature at each point in space-time. In contrast, the tensor variable with 'R' and two index values represents sixteen different numbers at each point in space-time, which are also related to curvature but provide more detailed information about the space-time structure.
Why is the space-time interval concept important in General Relativity?
-The space-time interval is important in General Relativity because it calculates the 'space-time interval' inside each infinitesimally small region using the metric tensor, which is crucial for understanding the effects of space-time curvature on measurements of distance and time.
How does the script explain the visualization of curved space-time?
-The script explains the visualization of curved space-time by describing it as a two-dimensional sheet embedded in a three-dimensional space that obeys Euclidean Geometry. However, it also notes that General Relativity does not require space-time to be embedded in a higher-dimensional space for the mathematics to work.
Outlines
🌌 Einstein's Field Equations and Space-Time Curvature
This paragraph introduces Einstein's Field Equations, which are fundamental to understanding the fabric of space-time and gravity. It explains how mass and momentum warp space-time, creating the phenomenon of gravity without the need for a force. The equations also account for gravitational waves, black holes, and the universe's accelerating expansion. The concept of space-time as a four-dimensional construct is discussed, with the first dimension being time and the remaining three being spatial dimensions. The paragraph also touches on the idea that space-time appears flat when observed at a small scale, similar to how the Earth looks flat from a limited vantage point. It delves into the mathematical approximation of flat space-time and how different observers may perceive space-time differently due to their relative motion, as dictated by Special Relativity. The process of navigating through space-time by adjusting for its curvature is also described, illustrating how objects follow curved paths that give the impression of being under the influence of gravity.
📚 Understanding Curvature and Basis Vectors in Space-Time
This paragraph delves deeper into the concept of space-time curvature by examining the behavior of basis vectors, which are fundamental to describing the local structure of space-time. It explains how these vectors can change due to the use of a curved coordinate system or an inherently curved space-time. The paragraph introduces the notion of parallel transport, a method of moving a vector across space-time while accounting for its curvature. It contrasts the behavior of vectors in flat versus curved space-time, highlighting that in the latter, a vector may not point in the same direction upon returning to its starting point after parallel transport. The concept of curvature is further explored by defining it in terms of the angle change of a vector when it completes a loop, with the angle change depending on the size of the enclosed area. The paragraph also introduces the idea of positive and negative curvature, providing the example of a saddle point to illustrate negative curvature.
🔍 Curvature Definition and Einstein's Field Equation Components
This paragraph refines the definition of space-time curvature by considering the limit as the enclosed area approaches zero, leading to a point-wise measure of curvature denoted by the scalar variable 'R'. It differentiates this scalar curvature from the tensor variable with two index values, which represents different numerical values at each point in space-time. The paragraph discusses the role of these tensors in Einstein's Field Equations and how they relate to the geometry of space-time, independent of the chosen coordinate system. It also explores the concept of the space-time interval, which is a measure of distance in space-time that all observers can agree upon, and how this concept is affected by the curvature of space-time. The metric tensor is introduced as a tool for calculating space-time intervals in curved space-time.
🌐 Exploring the Metric Tensor and Space-Time Curvature
The paragraph focuses on the metric tensor and its role in understanding the curvature of three-dimensional space, with an extension to four-dimensional space-time. It describes the process of parallel transporting a vector around an infinitesimal parallelogram in both flat and curved spaces, and how this process reveals the changes in the vector due to curvature. The concept of 'dV', representing changes in vector components, is introduced, along with a new variable 'R' with four index values, which helps in calculating these changes. The paragraph explains how this variable is used to compute terms in Einstein's Field Equations, which describe the relationship between the curvature of space-time and the distribution of energy and momentum.
🌌 Cosmological Constant and Energy-Momentum in Space-Time
This paragraph introduces the cosmological constant, which is a term in Einstein's Field Equations that governs the acceleration of the universe's expansion, associated with dark energy. It then shifts focus to the right side of the equation, discussing the constants and variables involved, such as the gravitational constant, the speed of light, and the stress-energy-momentum tensor. The paragraph explains how classical physics defines momentum and how it is modified in the context of special relativity to account for objects approaching the speed of light. It also extends the concept of momentum to four dimensions, allowing for the inclusion of phenomena like electromagnetic radiation. The paragraph concludes by discussing how the stress-energy-momentum tensor can be used to calculate the density of energy and momentum at each point in space-time.
📚 Stress-Energy-Momentum Tensor and Visualization of Curved Space-Time
The final paragraph discusses the stress-energy-momentum tensor, which represents the density of energy and momentum in space-time, including contributions from matter and electromagnetic radiation but not the energy of curved space-time itself. It explains how this tensor can be calculated from other defined values using the metric tensor. The paragraph also addresses the visualization of curved space-time as a two-dimensional sheet in a three-dimensional space, clarifying that such an embedding is not a requirement for the mathematics of General Relativity to be valid. It emphasizes that the universe may not be governed by Euclidean Geometry, indicating the complex and non-intuitive nature of space-time as described by Einstein's theories.
Mindmap
Keywords
💡Einstein’s Field Equations
💡Space-time
💡Gravitational Waves
💡Black Holes
💡Curvature
💡Coordinate System
💡Basis Vectors
💡Parallel Transport
💡Cosmological Constant
💡Stress-Energy-Momentum Tensor
💡Metric Tensor
Highlights
Einstein’s Field Equations describe the curvature of space-time caused by mass and momentum, which creates gravity.
The equations also account for phenomena like gravitational waves, black holes, and the accelerating expansion of the Universe.
Space-time is represented by two dimensions of space and two of time.
Curvature of space-time can appear flat when observing a small section, similar to how the Earth looks flat.
Flat space-time approximations use mathematical axes for spatial dimensions and time.
Different observers may have different axis orientations due to Special Relativity.
Rotating the observer's direction corrects the approximation for moving through space-time.
Repeated corrections using small time steps trace an object's path through curved space-time.
Four coordinates (X0, X1, X2, X3) are needed to describe four-dimensional space-time.
Einstein’s Field equations are valid regardless of the chosen coordinate system.
Basis vectors and their changes are crucial for understanding space-time geometry.
Curvature affects the rate of change of basis vectors in both flat and curved space-time.
Newtonian physics' approximations relate gravitational acceleration to space-time curvature.
Understanding vector changes due to curvature involves parallel transport.
Curvature is defined by the angle change of a vector when it returns to its original position.
Positive and negative curvatures are distinguished by the direction of vector rotation.
The scalar variable 'R' signifies the curvature at each point in Einstein’s Field Equation.
Tensor variables in the equations represent different numbers at each space-time point.
The relationship between tensors is fixed, but their values depend on the coordinate system.
The space-time interval, a concept from Special Relativity, is redefined in General Relativity using the metric tensor.
The cosmological constant represents the acceleration of the Universe's expansion, associated with dark energy.
The stress-energy-momentum tensor describes the density of energy and momentum in space-time.
General Relativity does not necessitate embedding space-time in higher dimensions for its mathematics.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: