Einstein Field Equations - for beginners!
TLDRThis script offers an introductory derivation of the Einstein Field Equations, simplifying complex concepts for beginners. It delves into the principles of equivalence and gravitational light bending, transitioning into the geometric interpretation of gravity as space-time curvature. The script introduces key concepts like the metric tensor, Christoffel symbols, and the Ricci tensor, ultimately leading to the Einstein Field Equations that relate space-time curvature to the distribution of mass-energy. The cosmological constant and stress-energy momentum tensor are also discussed, with references to Leonard Susskind's detailed lectures for further understanding.
Takeaways
- 📚 The script provides an introductory derivation of the Einstein Field Equations, a fundamental concept in general relativity, which describes the fabric of space-time and its interaction with mass and energy.
- 🔍 It emphasizes the importance of the principle of equivalence and the bending of light in a gravitational field, both key insights that led Einstein to propose general relativity.
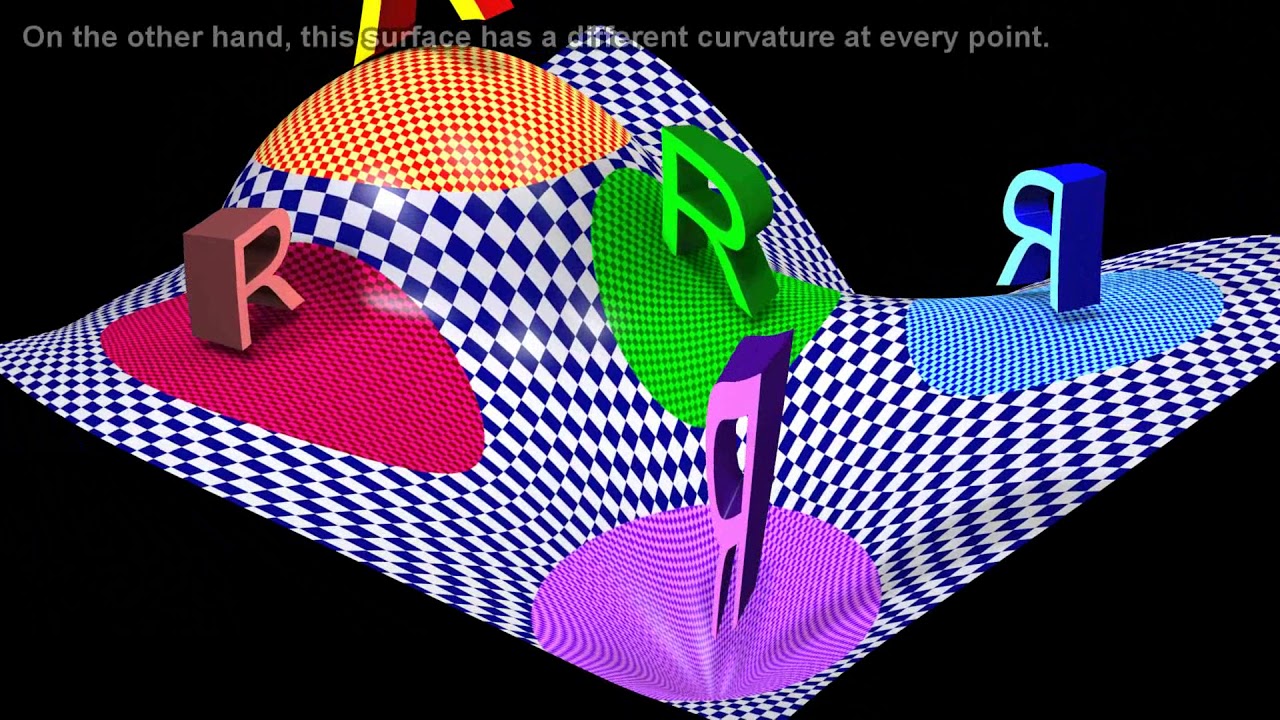
- 🌌 The script explains Einstein's perspective that gravity is not a force but a curvature of space-time caused by mass and energy, which is a shift from Newton's law of gravitation.
- 📐 The metric tensor, Ricci curvature tensor, and the curvature scalar are introduced as essential components in the formulation of the Einstein Field Equations, representing the geometry of space-time.
- 🔑 The Christoffel symbols are derived as crucial elements for understanding how vectors change direction when parallel transported around a curved space-time, which is not apparent in flat space-time.
- 💫 The script discusses the concept of geodesics, which are the shortest paths between two points in curved space-time, and their relevance to the motion of particles in a gravitational field.
- 📈 The stress-energy-momentum tensor, T μν, is described as a representation of the distribution and flow of energy and momentum in space-time, which is a source in the Einstein Field Equations.
- 🛰️ The cosmological constant, Λ, is introduced as a term in the Einstein Field Equations, initially included by Einstein to allow for a static universe, but later recognized as a key component in understanding cosmic acceleration.
- 🧩 The Einstein Field Equations are presented as a set of ten interrelated equations (reduced from sixteen due to symmetries) that govern the dynamics of space-time in the presence of matter and energy.
- 🔗 The script links the concepts of general relativity to the observable phenomena such as gravitational lensing and the precession of Mercury's orbit, demonstrating the practical implications of the theory.
- 🔬 It concludes by referencing Professor Leonard Susskind's lectures for a more in-depth study, acknowledging the complexity of the subject and the foundational role of Einstein's work in the field of theoretical physics.
Q & A
What are the Einstein field equations and why are they significant?
-The Einstein field equations are the fundamental equations of general relativity that describe the fundamental interaction of gravitation as a result of spacetime being curved by mass and energy. They are significant because they provide a theoretical framework for understanding gravity not as a force, but as a curvature of spacetime caused by mass and energy.
What is the principle of equivalence and how does it relate to the Einstein field equations?
-The principle of equivalence states that the laws of physics are the same for all observers in free fall, regardless of their velocity or position in space, and that the effects of gravity are indistinguishable from those of acceleration. This principle is foundational to the Einstein field equations, as it implies that gravitational and inertial forces are interchangeable.
What role does the metric tensor play in the Einstein field equations?
-The metric tensor, denoted as G_{μν}, is a fundamental component of the Einstein field equations. It encodes the geometry of spacetime and determines how distances are measured within it. The metric tensor is used to calculate the curvature of spacetime, which in turn is related to the distribution of mass and energy.
What is the cosmological constant and why was it introduced by Einstein?
-The cosmological constant, denoted by Λ (Lambda), was introduced by Einstein as a term in the Einstein field equations to allow for a static universe, counteracting the gravitational contraction predicted by his own equations. It represents a form of energy density that counteracts gravity on cosmological scales, and its modern interpretation is related to the observed acceleration of the expansion of the universe.
What is the stress-energy-momentum tensor and how does it relate to the distribution of mass and energy in spacetime?
-The stress-energy-momentum tensor, denoted as T_{μν}, is a tensor that describes the density and flux of mass, energy, and momentum within spacetime. It is used in the Einstein field equations to represent the source of the gravitational field, with the distribution of mass and energy determining the curvature of spacetime.
What is the difference between a covariant and a contravariant transformation of a tensor?
-A covariant transformation involves lowering the indices of a tensor when transforming from one coordinate system to another, and it involves terms with the differential of the new coordinates with respect to the old coordinates. A contravariant transformation involves raising the indices and uses terms with the differential of the old coordinates with respect to the new coordinates. The covariant derivative includes the Christoffel symbols to account for curvature in spacetime.
What are Christoffel symbols and how do they relate to the curvature of spacetime?
-Christoffel symbols, denoted as Γ^α_{μν}, are mathematical objects that describe the difference between the covariant derivative and the partial derivative in curved spacetime. They are used to express the change in the direction of a vector as it is parallel transported around a curved surface, which is a measure of the curvature of that spacetime.
What is the Ricci curvature tensor and how is it derived?
-The Ricci curvature tensor, denoted as R_{μν}, is derived from the Riemann curvature tensor by contracting two of its indices. It provides a measure of the curvature of spacetime and is a key component of the Einstein field equations. The Ricci tensor is obtained by summing over one index of the Riemann tensor, weighted by the metric tensor.
What is the curvature scalar and how is it related to the Ricci tensor?
-The curvature scalar, denoted as R, is a scalar quantity that is derived from the Ricci tensor by taking its trace, which involves summing over both indices of the Ricci tensor. The curvature scalar provides a single measure of the curvature of spacetime and is used in the Einstein field equations as part of the Einstein tensor.
What is the significance of the geodesic in the context of general relativity?
-In general relativity, a geodesic is the shortest path between two points in spacetime, taking into account the curvature caused by mass and energy. It represents the trajectory that a particle would follow in the absence of any external forces, and it is used to describe the motion of objects in a gravitational field.
Outlines
Introduction to Deriving Einstein's Field Equations
The speaker introduces the plan to derive Einstein's field equations in a simplified manner, following the approach of Professor Leonard Susskind. Key assumptions include knowledge of calculus, basic geometry, and general relativity principles, particularly the principle of equivalence and light bending in gravitational fields.
Historical Proof of Light Bending
The speaker explains the historical proof of Einstein's theory during a solar eclipse, where light from a star behind the Sun appeared bent due to the Sun's gravitational field. This observation challenged Newton's laws, as photons have no mass, leading Einstein to propose a new approach to gravity involving curved space-time.
Introduction to Curved Space-Time
Einstein's new approach suggested that gravity is not a force but a result of the curvature of space-time caused by mass. The analogy of a trampoline with a heavy object creating a dent illustrates how objects move along the shortest paths in curved space-time, altering our understanding of orbits and gravity.
Explaining Space-Time
The concept of space-time as a combination of three spatial dimensions and one time dimension is introduced. The speaker explains how constant velocity appears as a straight line in space-time, while acceleration results in a curve, further supporting the idea that gravity curves space-time.
Geometric Interpretation of Fields
Using a bumpy field as an example, the speaker discusses how the height of the field changes based on the direction of movement. This introduces the concept of gradients and partial derivatives to understand variations in a field, setting the stage for more complex tensor calculus.
Introduction to Tensors
The concept of tensors is introduced, starting with scalars (rank 0 tensors) and vectors (rank 1 tensors). The speaker explains how tensors of rank 2, which are combinations of vectors, transform between coordinate systems using the chain rule and partial derivatives.
Vector Transformation and Tensors of Rank 2
The speaker elaborates on the transformation properties of vectors and introduces tensors of rank 2, which combine vectors. This involves understanding the transformation rules and how tensors maintain fixed relationships across different frames of reference.
Physical Interpretation of Tensors
A practical example involving a block on the floor is used to explain tensors of rank 2. The work done by a force moving the block is considered, illustrating how tensors represent relationships between vectors that are invariant across reference frames.
Contravariant and Covariant Transformations
The distinction between contravariant and covariant transformations of tensors is made. Contravariant transformations involve indices 'upstairs,' while covariant transformations involve indices 'downstairs.' These transformations are crucial for understanding how tensors change between coordinate systems.
Revisiting Pythagoras in Curved Space
Pythagoras' theorem is revisited in the context of curved space. The speaker introduces the Kronecker delta to handle cross terms in the metric tensor, which corrects Pythagoras' theorem for curved spaces, illustrating how geometry changes in general relativity.
Metric Tensor and Curved Space-Time
The metric tensor is defined as the correction term for Pythagoras' theorem in curved space-time. It accounts for the curvature of space-time and is fundamental to the Einstein field equations, especially when dealing with non-flat geometries.
Covariant Derivative and Christoffel Symbols
The need for covariant derivatives in tensor calculus is emphasized. Ordinary derivatives do not transform properly between reference frames, necessitating the use of Christoffel symbols to correct for curvature and ensure proper tensor transformation.
Derivation of Christoffel Symbols
The speaker derives the Christoffel symbols, showing how they are related to the metric tensor and its derivatives. These symbols are essential for expressing the covariant derivative and understanding the geometry of curved space-time.
Tensor Transformation with Christoffel Symbols
The transformation properties of tensors involving Christoffel symbols are discussed. The covariant derivative of tensors is explored in detail, showing how these derivatives ensure proper transformation between different coordinate systems.
Geodesics and the Metric Tensor
The concept of geodesics, or the shortest paths in curved space-time, is introduced. The speaker explains how the covariant derivative of the metric tensor is zero in all frames of reference, emphasizing the invariance of geometric relationships in general relativity.
Measuring Curvature: Parallel Transport
Curvature is explained using the parallel transport of vectors. A vector transported around a curved surface changes direction, indicating curvature. This forms the basis for understanding how space-time curvature affects the motion of objects.
Commutators and Their Importance
Commutators, which measure the difference in applying two operations in different orders, are introduced. The speaker shows how commutators are used to understand the behavior of derivatives and their role in defining curvature.
Curvature and Parallel Transport
Parallel transport around a parallelogram is used to illustrate curvature. The difference in vectors after transport indicates curvature, and this concept is related to the commutator of covariant derivatives, leading to the definition of the Riemann tensor.
The Riemann Tensor
The Riemann tensor, which encapsulates the curvature of space-time, is introduced. It is derived from the Christoffel symbols and their derivatives. The speaker explains how the Riemann tensor is related to the Ricci tensor, essential for Einstein's field equations.
The Ricci Tensor and Curvature Scalar
The Ricci tensor, derived from the Riemann tensor, and the curvature scalar are defined. These quantities measure the curvature of space-time and are crucial components of the Einstein field equations, linking geometry with physical phenomena.
Geodesics and the Stress-Energy Tensor
Geodesics are explored in the context of the stress-energy tensor. The speaker explains how the covariant derivative of the tangent vector along a geodesic relates to the Christoffel symbols and the equivalence of gravitational and inertial mass.
Einstein's Field Equations and the Stress-Energy Tensor
The derivation of the stress-energy tensor, which embodies energy, momentum, stress, and pressure, is discussed. This tensor is central to Einstein's field equations, linking the curvature of space-time with the distribution of mass and energy.
Newtonian Gravity and General Relativity
The relationship between Newtonian gravity and general relativity is explored. The speaker shows how general relativity reduces to Newtonian gravity in the low-speed, weak-field limit, using the time component of the metric tensor to bridge the two theories.
The Einstein Field Equations
The Einstein field equations are derived, combining the Ricci tensor, metric tensor, and stress-energy tensor. The inclusion of the cosmological constant is discussed, highlighting its role in balancing gravitational attraction and explaining the expansion of the universe.
Conclusion
The speaker concludes by summarizing the key components of Einstein's field equations and their significance in linking mass-energy with the curvature of space-time. A reference to Professor Leonard Susskind's lectures is provided for further detailed study.
Mindmap
Keywords
💡Einstein Field Equations
💡Principle of Equivalence
💡Gravitational Field
💡Metric Tensor
💡Christoffel Symbols
💡Ricci Curvature Tensor
💡Cosmological Constant
💡Stress-Energy Momentum Tensor
💡Covariant Derivative
💡Geodesic
Highlights
Introduction to deriving Einstein field equations with a simplified approach compared to Leonard Susskind's lectures.
Assumption of understanding calculus, basic geometry, and principles of equivalence and light bending in a gravitational field.
Explanation of the principle of equivalence and its implications for distinguishing between acceleration and gravity.
Einstein's reasoning for light bending in a gravitational field due to acceleration.
The problem with Newton's law of gravitation when applied to light, leading to Einstein's new approach to gravity.
Introduction of the concept of space-time as a four-dimensional set of coordinates.
Einstein's view of gravity as motion in curved space-time rather than a force.
Overview of the Einstein field equations as a balance between space-time curvature and mass-energy.
Introduction of key terms in the Einstein field equations: Ricci curvature tensor, metric tensor, curvature scalar, cosmological constant, and stress-energy-momentum tensor.
Explanation of the metric tensor and its role in describing the geometry of space-time.
Derivation of the metric tensor from the concept of a field and its transformation between different coordinate systems.
Introduction to tensors as relationships between vectors that remain constant across different frames of reference.
Explanation of rank-2 tensors and their significance in the Einstein field equations.
Derivation of the Christoffel symbols as correction terms for the covariant derivative of tensors.
Introduction to the concept of curvature and its relation to parallel transport of vectors.
Derivation of the Riemann tensor as a measure of curvature in space-time.
Explanation of the relationship between the Ricci tensor and the curvature of space-time.
Introduction to the stress-energy-momentum tensor as a representation of energy and momentum in space-time.
Derivation of the Einstein field equations incorporating the stress-energy-momentum tensor and the cosmological constant.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: