AP Physics B Kinematics Presentation #51

The New Jersey Center for Teaching and Learning
26 Jun 201203:25
EducationalLearning
32 Likes 10 Comments

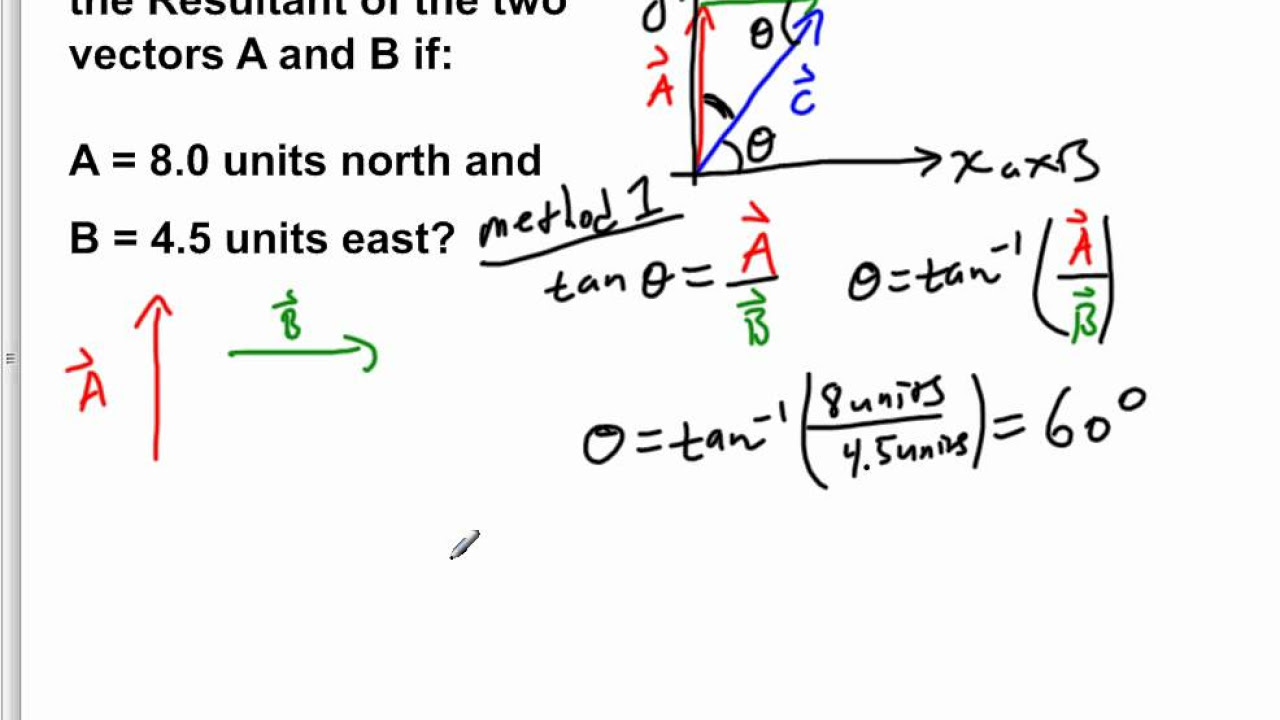
TLDRThe video script demonstrates the process of finding the direction of the resultant vector from two given vectors, a and b. Vector a is 400 units north, and vector b is 250 units east. Using the tail-to-tip method, the resultant vector is graphically represented. By introducing an x-axis and y-axis, the angle of the resultant vector with the x-axis is determined using trigonometry, specifically the tangent function. The angle is calculated to be approximately 60 degrees, providing the direction of the resultant vector relative to the horizontal axis.

Takeaways
  • 📍 The task is to find the direction of the resultant of two vectors, a and b, where a is 400 units north and b is 250 units east.
  • 📈 The tail-to-tip method is used to graphically represent the addition of vectors a and b to find the resultant vector.
  • 📏 The resultant vector is drawn on the same scale as the vectors a and b to visualize its direction and magnitude.
  • 📉 The x-axis and y-axis are introduced to the diagram to facilitate the calculation of the angle the resultant vector makes with the x-axis.
  • 🔍 The angle between the resultant vector and the x-axis is determined by using the geometric property of similar triangles.
  • 📐 The tangent of the angle (theta) is calculated as the ratio of the opposite side (vector a) to the adjacent side (vector b).
  • 🧭 The arctangent function is used to find the angle theta, which is the direction of the resultant vector with respect to the x-axis.
  • 🔢 The values of vector a (400 units) and vector b (250 units) are substituted into the arctangent function to calculate the angle.
  • 📊 The calculated angle is approximately 60 degrees, indicating the direction of the resultant vector relative to the x-axis.
  • 📝 The process involves both graphical representation and mathematical calculation to determine the direction of the resultant vector.
  • 📚 Understanding the properties of geometry and trigonometry is essential for solving the problem of vector addition and finding the resultant direction.
Q & A

  • What are the two vectors mentioned in the script?

    -The two vectors mentioned are vector a, which is 400 units to the north, and vector b, which is 250 units to the east.

  • What method is used to find the resultant of the two vectors?

    -The tail to tip method is used to find the resultant of the two vectors.

  • How is the resultant vector represented visually in the script?

    -The resultant vector is represented by drawing an arrow from the tail of vector a to the tip of vector b, showing its direction and magnitude.

  • What axes are introduced to help find the direction of the resultant vector?

    -The x-axis and the y-axis are introduced to help find the direction of the resultant vector.

  • What geometric property is used to find the angle the resultant vector makes with the x-axis?

    -The geometric property that the angle is the same at the top and bottom of the right triangle formed by the vectors is used to find the angle the resultant vector makes with the x-axis.

  • What trigonometric function is used to solve for the angle theta?

    -The tangent function (tan) is used to solve for the angle theta, where tan(theta) is equal to the opposite side over the adjacent side.

  • How is the angle theta calculated in the script?

    -The angle theta is calculated using the arctangent (tan inverse) of the ratio of vector a to vector b, which is 400 units over 250 units.

  • What is the approximate angle that the resultant vector makes with the x-axis?

    -The approximate angle that the resultant vector makes with the x-axis is 60 degrees.

  • Why is the secant method not used to solve for theta in this case?

    -The secant method is not used because the tangent function is more appropriate for the given situation, as it directly relates to the ratio of the opposite side to the adjacent side in a right triangle.

  • What does the direction of the resultant vector represent in the context of the script?

    -The direction of the resultant vector represents the overall direction that the combined effect of the two vectors a and b would take.

  • How does the magnitude of the resultant vector relate to the magnitudes of vectors a and b?

    -The magnitude of the resultant vector is determined by the vector addition of a and b, and it can be calculated using the Pythagorean theorem if needed.

Outlines
00:00
📐 Vector Resultant Direction Calculation

This paragraph explains the process of finding the direction of the resultant vector when two vectors, 'a' and 'b', are given. Vector 'a' is 400 units to the north, and vector 'b' is 250 units to the east. The method involves visualizing both vectors and then using the tail-to-tip method to draw the resultant vector. An axis system is introduced to determine the angle the resultant vector makes with the x-axis. The angle is found by using the tangent inverse function of the ratio of vector 'a' to vector 'b', which yields approximately 60 degrees with respect to the x-axis. This angle represents the direction of the resultant vector.

Mindmap
Keywords
💡Resultant Vector
A resultant vector is the vector sum of two or more vectors. It represents the combined effect of the individual vectors when they are added together. In the video, the resultant vector is found by adding vector 'a', which points north, and vector 'b', which points east. The script describes the process of finding the magnitude and direction of this resultant vector using the tail-to-tip method.
💡Tail-to-Tip Method
The tail-to-tip method is a graphical technique used to find the resultant of two vectors by placing the tail of the second vector at the tip of the first and then drawing the vector from the tail of the first to the tip of the second. The script uses this method to visually represent the addition of vector 'a' and 'b', resulting in the resultant vector.
💡Magnitude
Magnitude refers to the length or size of a vector, which corresponds to its strength or the distance it represents. In the context of the video, the magnitude of the resultant vector is determined through the graphical representation after adding vectors 'a' and 'b'.
💡Direction
Direction in vector terms is the angle a vector makes with a reference axis, typically the positive x-axis. The video script discusses finding the direction of the resultant vector by determining the angle it makes with the x-axis, which is crucial for understanding the overall orientation of the vector sum.
💡North
In the script, 'north' is used to describe the direction of vector 'a', which is 400 units long. It is one of the cardinal directions and is used here to establish the initial orientation of one of the vectors being added.
💡East
Similar to 'north', 'east' is a cardinal direction used in the script to define the direction of vector 'b', which is 250 units long. It helps to establish the orientation of the second vector in the vector addition process.
💡Axis
An axis, particularly the x-axis and y-axis mentioned in the script, serves as a reference for determining the direction of a vector. The x-axis is horizontal, and the y-axis is vertical in a standard Cartesian coordinate system, which is used to analyze the angle of the resultant vector.
💡Angle
The angle is a measure of the space between two lines or planes that intersect. In the video, the angle is used to describe the direction of the resultant vector in relation to the x-axis. The script calculates this angle using trigonometric functions to find the orientation of the combined vector.
💡Tangent
The tangent of an angle in a right-angled triangle is the ratio of the length of the opposite side to the length of the adjacent side. In the script, the tangent function is used to calculate the angle 'theta' that the resultant vector makes with the x-axis by using the lengths of vectors 'a' and 'b'.
💡Tan Inverse
The inverse tangent function, often abbreviated as 'tan inverse' or 'arctan', is used to find the angle when the ratio of the opposite side to the adjacent side is known. In the script, tan inverse is applied to find the angle of the resultant vector by taking the inverse of the tangent of the ratio of vector 'a' to vector 'b'.
💡Trigonometry
Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles. The script uses trigonometric principles, specifically the tangent and its inverse, to solve for the angle of the resultant vector, illustrating the application of trigonometry in vector analysis.
Highlights

Vectors a and b are defined with a pointing 400 units north and b pointing 250 units east.

The tail to tip method is used to visualize the resultant vector.

The resultant vector is drawn by adding vector b to vector a.

An axis system is introduced to determine the direction of the resultant vector.

The geometric property of equal angles is utilized to find the angle of the resultant vector.

The angle of the resultant vector is calculated using the tangent function.

The tangent inverse function is applied to find the angle with respect to the x-axis.

The values of vectors a and b are substituted into the tangent inverse formula.

The resultant vector makes an angle of approximately 60 degrees with the x-axis.

The direction of the resultant vector is determined to be at a 60-degree angle to the x-axis.

The process involves a clear step-by-step approach to finding the resultant vector's direction.

The method demonstrates the practical application of vector addition and geometric principles.

The use of the tail to tip method simplifies the visualization of vector addition.

The introduction of an axis system aids in the precise measurement of angles.

The transcript provides a clear explanation of how to calculate the angle of a resultant vector.

The final result is a practical example of the application of trigonometry in vector analysis.

The process concludes with a clear understanding of the resultant vector's direction in relation to the x-axis.

Transcripts

Browse More Related Video

AP Physics B Kinematics Presentation #48

AP Physics B Kinematics Presentation #49

AP Physics B Kinematics Presentation General Problems #08

AP Physics B Kinematics Presentation #47

AP Physics B Kinematics Presentation #50

AP Physics B Kinematics Presentation #46

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Vector AnalysisDirection CalculationGeometric MethodResultant VectorTangent FunctionAngle MeasurementNorth VectorEast VectorCartesian PlaneTrigonometry Basics