AP Physics B Kinematics Presentation #50
TLDRThis script demonstrates the process of finding the magnitude of the resultant vector when two vectors, A and B, are combined. Vector A is 400 units north, and B is 250 units east. By applying the Pythagorean theorem, the script explains how to calculate the magnitude of the resultant vector C, which is the hypotenuse of the right triangle formed by A and B. The calculation involves squaring the magnitudes of A and B, summing them, and then taking the square root of the result, yielding an approximate magnitude of 472 units for the resultant vector C.
Takeaways
- 📏 Vector A is represented as 400 units north.
- 📐 Vector B is represented as 250 units east.
- 📍 The resultant vector C is found by adding vectors A and B using the tail-to-tip method.
- 🔍 The Pythagorean theorem is applied to find the magnitude of the resultant vector C.
- 🧮 The formula for magnitude is C = \( \sqrt{A^2 + B^2} \), where A and B are the magnitudes of the vectors.
- 🔢 The calculation involves squaring the magnitudes of A and B, which are 400 and 250 respectively.
- 📉 Squaring 400 gives 160,000 square units, and squaring 250 gives 62,500 square units.
- 📈 Adding these squared values results in 222,500 square units.
- 📌 The square root of 222,500 gives the magnitude of the resultant vector C.
- 📝 The magnitude of the resultant vector C is approximately 472 units.
- 📚 The tail-to-tip method is used to graphically represent the addition of vectors and find the resultant.
Q & A
What are the two vectors mentioned in the script?
-The two vectors mentioned are vector A, which is 400 units north, and vector B, which is 250 units east.
What is the purpose of drawing vector A and B?
-Drawing vector A and B helps to visually represent the vectors and understand how they will be combined to find the resultant vector.
What method is used to add the vectors A and B?
-The tail-to-tip method is used to add vectors A and B, which involves placing the tail of one vector at the tip of the other and observing the resultant vector formed.
What is the direction of the resultant vector C after adding A and B?
-The resultant vector C is in a direction that is neither purely north nor purely east, but somewhere in between, as determined by the tail-to-tip method.
How is the magnitude of the resultant vector C calculated?
-The magnitude of the resultant vector C is calculated using the Pythagorean theorem, where C squared equals A squared plus B squared, and then taking the square root of the sum.
What is the Pythagorean theorem in the context of vector addition?
-In the context of vector addition, the Pythagorean theorem states that the square of the magnitude of the resultant vector (C squared) is equal to the sum of the squares of the magnitudes of the individual vectors (A squared plus B squared).
What mathematical operation is performed after squaring the magnitudes of vectors A and B?
-After squaring the magnitudes of vectors A and B, the values are added together to find the sum, which is then used to find the magnitude of the resultant vector C.
What is the calculated magnitude of the resultant vector C in the script?
-The calculated magnitude of the resultant vector C is approximately 472 units.
Why is the magnitude of the resultant vector important?
-The magnitude of the resultant vector is important as it gives the total strength or length of the combined vector, which can be crucial in various applications such as physics, engineering, and navigation.
Can the method demonstrated in the script be applied to vectors with different magnitudes or directions?
-Yes, the method demonstrated can be applied to vectors of any magnitude and direction, as long as the vectors are in two dimensions and the goal is to find the resultant vector.
What is the significance of the signs when squaring the magnitudes of vectors A and B?
-The signs are not significant when squaring the magnitudes of vectors A and B because squaring a number always results in a positive value, regardless of whether the original number was positive or negative.
Outlines
📏 Vector Addition and Magnitude Calculation
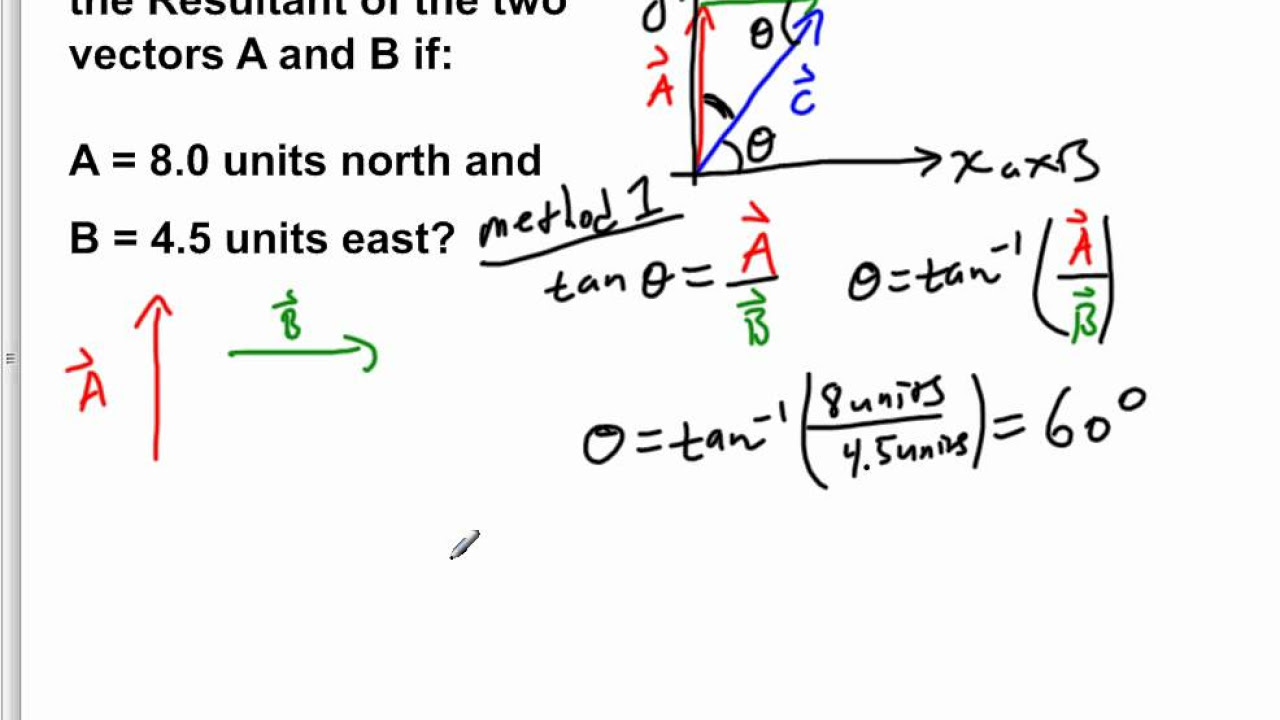
This paragraph explains the process of finding the magnitude of the resultant vector when two vectors, a and B, are given. Vector a is described as 400 units north, and vector B as 250 units east. The tail-to-tip method is used to visualize the addition of these vectors, resulting in a new vector C. The magnitude of C is calculated using the Pythagorean theorem, where C squared equals the sum of the squares of a and B. After substituting the given values, the calculation leads to the magnitude of C being approximately 472 units.
Mindmap
Keywords
💡Magnitude
💡Resultant
💡Vector A
💡Vector B
💡Tail-to-Tip Method
💡Pythagorean Theorem
💡Square Root
💡North
💡East
💡Units
💡Approximately
Highlights
Finding the magnitude of the resultant of two vectors A and B.
Vector A is 400 units north.
Vector B is 250 units east.
Using the tail to tip method to add vectors A and B.
Resultant vector C is in a different direction.
Applying the Pythagorean theorem to find the magnitude of C.
C squared is equal to A squared plus B squared.
C is equal to the square root of A squared plus B squared.
Plugging in values for A and B to calculate C.
A squared is 160,000 square units.
B squared is 62,500 square units.
Adding A squared and B squared to get 222,500 square units.
Taking the square root of 222,500 to find the magnitude of C.
Magnitude of C is approximately 472 units.
Resultant vector C is found using the tail to tip method.
The process demonstrates vector addition and the Pythagorean theorem.
Practical application of vector mathematics in determining resultant magnitude.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: