AP Physics B Kinematics Presentation #49
TLDRThe video script explains the concept of finding the resultant vector of two given vectors, A and B, with magnitudes 24 units East and 15 units South, respectively. It uses the tail-to-tip method to visualize the resultant vector C. The script then demonstrates how to calculate the angle of the resultant vector with respect to the x-axis, using the tangent inverse function. The final answer is presented as 32° below the x-axis, which can also be expressed as 328° with respect to the x-axis, emphasizing the importance of distinguishing the direction for accurate vector analysis.
Takeaways
- 📏 The problem involves finding the direction of the resultant vector of two vectors A and B with given magnitudes and directions.
- 🧭 Vector A has a magnitude of 24 units and is directed towards the East.
- 🏔 Vector B has a magnitude of 15 units and is directed towards the South.
- 🔍 The resultant vector C is found by adding vectors A and B using the tail-to-tip method.
- 📐 The direction of the resultant vector C is determined by calculating the angle Theta with respect to the x-axis.
- 📈 The tangent of Theta is calculated using the opposite (Vector B) over the adjacent (Vector A).
- 🔢 The values for Vector A and B are 24 and 15 units, respectively, which are plugged into the tangent function.
- 📲 The angle Theta is found by taking the arctan (inverse tangent) of the ratio of Vector B to Vector A.
- 📉 Theta is calculated to be 32° below the x-axis.
- 🔄 To find the angle with respect to the x-axis, the full circle of 360° is considered, and 32° is subtracted from it.
- 📌 The final answer for the direction of the resultant vector C with respect to the x-axis is 328°, or alternatively, it can be described as 32° below the x-axis.
Q & A
What are the magnitudes of vectors A and B as described in the transcript?
-Vector A has a magnitude of 24 units, directed East, and Vector B has a magnitude of 15 units, directed South.
What is the concept of the resultant vector when adding two vectors?
-The resultant vector is the vector that represents the combined effect of two or more vectors when they are added together.
What method is mentioned in the transcript for determining the direction of the resultant vector?
-The tail-to-tip method is mentioned for determining the direction of the resultant vector.
How is the angle theta related to the vectors A and B in the context of the resultant vector?
-Theta is the angle that the resultant vector makes with the horizontal axis (x-axis), which can be calculated using the components of vectors A and B.
What trigonometric function is used to find the angle theta in the context of the resultant vector?
-The tangent function (tan) is used to find the angle theta, where tan(theta) = opposite/adjacent, with the opposite being the magnitude of Vector B and the adjacent being the magnitude of Vector A.
What is the value of tan(theta) according to the given magnitudes of vectors A and B?
-The value of tan(theta) is the ratio of the magnitude of Vector B (15 units) to the magnitude of Vector A (24 units).
How do you find the angle theta from the calculated value of tan(theta)?
-The angle theta is found by taking the inverse tangent (tan^-1) of the calculated value of tan(theta).
What is the calculated angle theta in degrees?
-The calculated angle theta is 32° below the x-axis.
How can the angle with respect to the x-axis be expressed differently while maintaining the same meaning?
-The angle with respect to the x-axis can also be expressed as 328° with respect to the x-axis, which means it is 32° below the x-axis.
Why is it important to distinguish the direction of the angle with respect to the x-axis?
-Distinguishing the direction of the angle with respect to the x-axis is important to accurately describe the orientation of the resultant vector in a two-dimensional plane.
What is the significance of the angle completing a full cycle being 360° in the context of the problem?
-The significance is that it helps to determine the angle with respect to the x-axis by subtracting the angle below the x-axis from 360°, ensuring the angle is correctly oriented in the circle.
Outlines
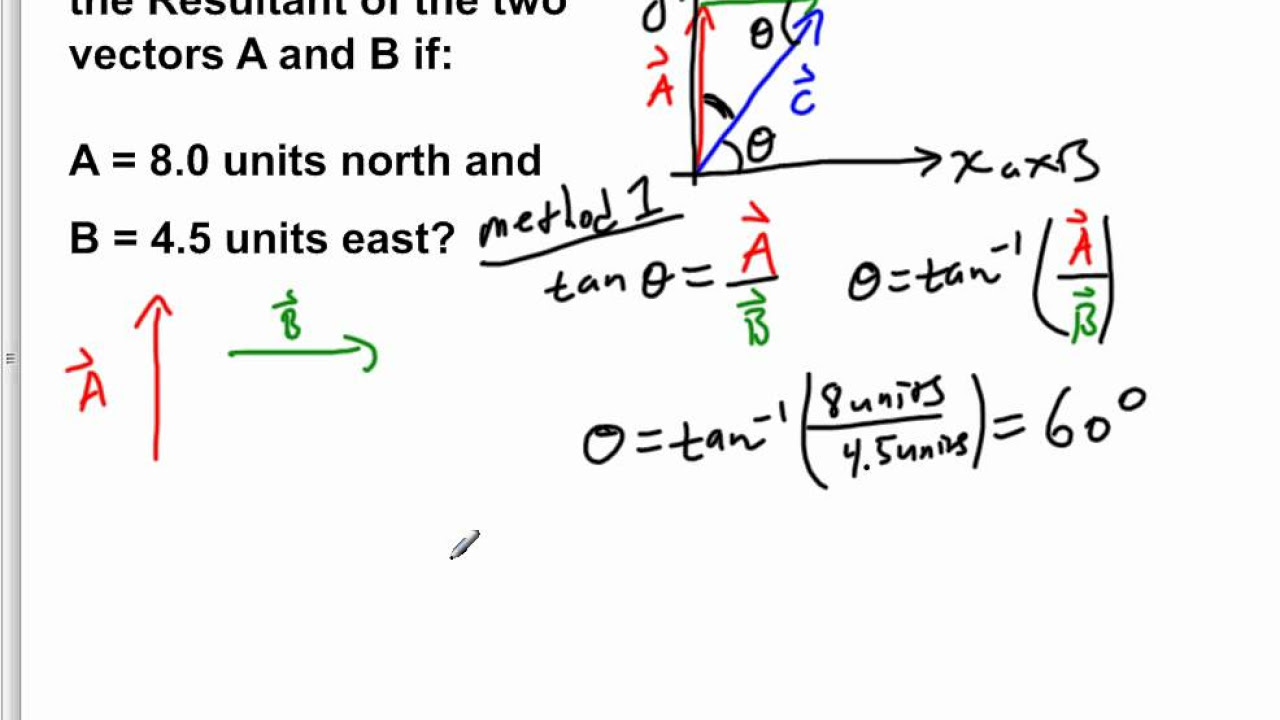
📚 Vector Addition and Direction Calculation
This paragraph explains the process of finding the direction of the resultant vector when adding two vectors, A and B. Vector A is given as 24 units East, and Vector B as 15 units South. The script uses the tail-to-tip method to visualize the addition and introduces the concept of calculating the angle theta (Θ) using the tangent function, where tan(Θ) = opposite/adjacent. The values for Vector B over Vector A are substituted into the formula to find Θ = 32°. The paragraph also discusses how to interpret this angle with respect to the x-axis, concluding that the resultant vector is 32° below the x-axis or alternatively, 328° with respect to the x-axis.
Mindmap
Keywords
💡Resultant
💡Vector A
💡Vector B
💡Tailor Tip Method
💡Theta
💡Tangent
💡Arctangent
💡Magnitude
💡Direction
💡Right-Angled Triangle
💡360° Cycle
Highlights
Two vectors A and B are defined with A pointing 24 units East and B pointing 15 units South.
The resultant vector C is calculated using the tail-to-tip method by adding vectors A and B.
A Cartesian coordinate system is used with the x-axis and y-axis to visualize the vectors.
Theta is the angle that the resultant vector C makes with the x-axis.
The tangent of theta is calculated as the ratio of the opposite side (vector B) to the adjacent side (vector A).
The arctangent function is used to find the angle theta by taking the inverse tangent of the ratio.
The values of vectors A (24 units) and B (15 units) are substituted into the formula to calculate theta.
Theta is found to be 32 degrees below the x-axis by taking the arctangent of 15/24.
The angle with respect to the x-axis is calculated by subtracting 32 degrees from 360 degrees, resulting in 328 degrees.
The final answer for the direction of the resultant vector C is 32 degrees below the x-axis or equivalently 328 degrees with respect to the x-axis.
The importance of distinguishing the angle's orientation with respect to the x-axis is emphasized.
The method used in the transcript is a practical application of vector addition and trigonometry.
The tail-to-tip method provides an intuitive way to visualize and calculate the resultant vector.
The use of the arctangent function is a key step in determining the angle theta.
The transcript demonstrates the process of converting a geometric problem into a mathematical one using vectors.
The final answer is presented in two equivalent forms to provide clarity and understanding.
The transcript provides a step-by-step explanation of the vector addition process, making it accessible for learners.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: