AP Physics B Kinematics Presentation General Problems #08
TLDRThis script details a step-by-step process of vector addition to find the resultant displacement of a ship's movements. It involves calculating the individual displacement vectors, determining their X and Y components using trigonometric functions, and then combining them to find the magnitude and direction of the resultant vector. The explanation is methodical, utilizing the tail-to-tip method for vector addition and the Pythagorean theorem for magnitude calculation, culminating in a resultant vector of approximately 55 miles at 65 degrees to the horizontal axis.
Takeaways
- 🚢 The script describes the process of calculating the resultant displacement vector of a ship after making three directional movements.
- 📏 The first displacement vector is 176 miles at 48 degrees north of East.
- 🔵 The second displacement vector is 250 miles at 56 degrees north of West.
- 🔺 The third displacement vector is 47 miles straight south.
- 📝 The script emphasizes the use of the tail-to-tip method for vector addition.
- 📈 The resultant vector is found by connecting the starting point back to the endpoint of the third vector.
- 🧭 The direction of each vector is calculated using trigonometric functions based on the given angles.
- 📐 The x and y components of each displacement vector are calculated using the cosine and sine of the respective angles.
- 🔢 The magnitude of the resultant vector is found using the Pythagorean theorem by summing the squares of the x and y components.
- 📊 The direction of the resultant vector is determined using the tangent function and the inverse tangent (arctan).
- 📉 The final calculated magnitude of the resultant vector is approximately 55 miles, and its direction is 65 degrees from the x-axis.
Q & A
What is the first displacement vector in the script?
-The first displacement vector is 176 miles at 48 degrees north of East.
What is the second displacement vector?
-The second displacement vector is 250 miles at 56 degrees north of West.
What is the magnitude and direction of the third displacement vector?
-The third displacement vector has a magnitude of 47 miles and is directed straight south.
How is the resultant vector determined in the script?
-The resultant vector is determined by adding all three displacement vectors using the tail-to-tip method and then connecting the starting point to the final point of the last vector.
What mathematical method is used to find the X and Y components of each displacement vector?
-The script uses the SOHCAHTOA method to find the X and Y components of each displacement vector.
What is the X component of the first displacement vector (D1)?
-The X component of D1 is 51 miles, calculated using the cosine of 48 degrees with the magnitude of 176 miles.
What is the Y component of the first displacement vector (D1)?
-The Y component of D1 is 56 miles, calculated using the sine of 48 degrees with the magnitude of 176 miles.
What is the direction of the second displacement vector (D2) in terms of the horizontal axis?
-The direction of D2 is 56 degrees north of West with respect to the horizontal axis.
What is the magnitude of the X component of the second displacement vector (D2)?
-The magnitude of the X component of D2 is -28 miles, indicating it points in the negative X direction.
What is the magnitude of the Y component of the second displacement vector (D2)?
-The magnitude of the Y component of D2 is 41 miles, pointing in the positive Y direction.
How is the magnitude of the resultant vector calculated?
-The magnitude of the resultant vector is calculated using the Pythagorean theorem, by taking the square root of the sum of the squares of the X and Y components of all vectors.
What is the magnitude of the resultant vector?
-The magnitude of the resultant vector is approximately 55 miles.
How is the direction of the resultant vector determined?
-The direction of the resultant vector is determined by using the tangent function, which is the ratio of the sum of the Y components to the sum of the X components, and then taking the inverse tangent (arctan) of that ratio.
What is the direction of the resultant vector with respect to the x-axis?
-The direction of the resultant vector with respect to the x-axis is 65 degrees.
Outlines
🚢 Vector Diagram Explanation
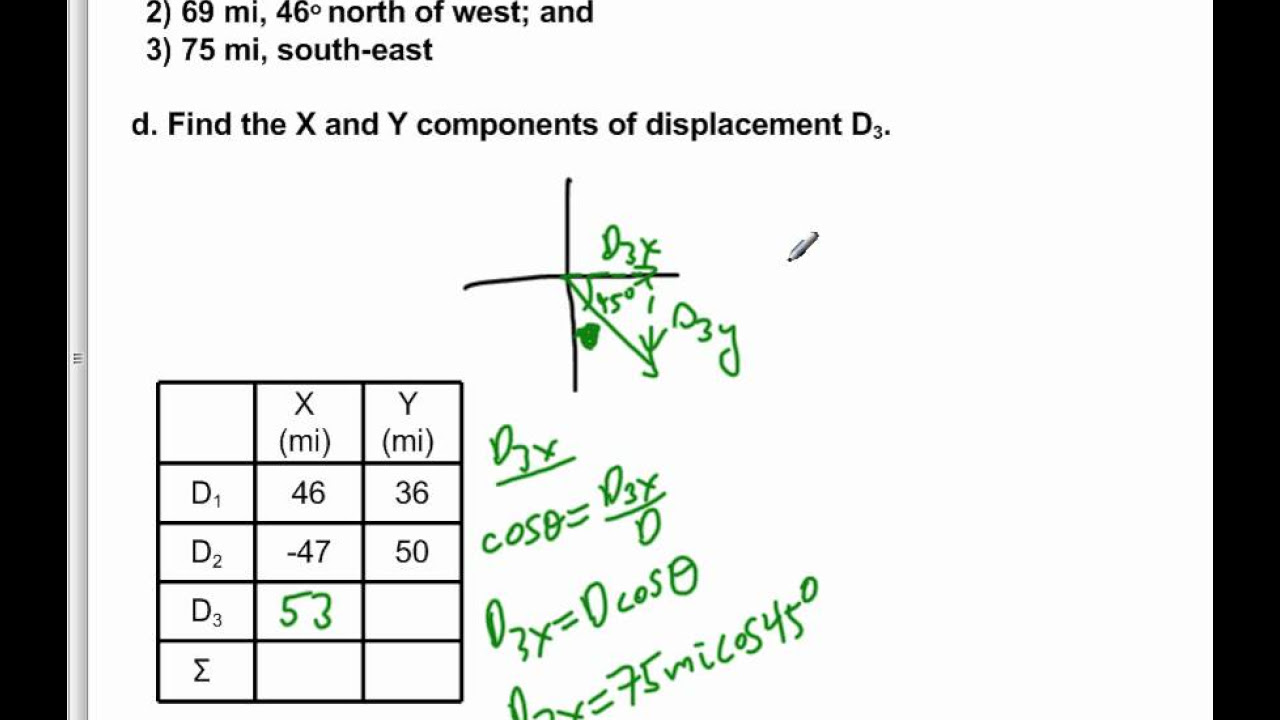
This paragraph describes the process of creating a diagram for three displacement vectors. The first vector is 176 miles at 48 degrees north of East, the second is 250 miles at 56 degrees north of West, and the third is 47 miles directly south. The paragraph explains how to draw these vectors with respect to the horizontal points north, east, south, and west, and how to calculate the resultant vector using the tail-to-tip method. It also introduces the concept of finding the X and Y components of displacement using trigonometric functions like cosine and sine.
📐 Calculating Displacement Components
This section details the calculation of the X and Y components for the first two displacement vectors, D1 and D2, using the SOHCAHTOA trigonometric method. For D1, the X component is found to be 51 miles and the Y component is 56 miles. For D2, the X component is calculated as -28 miles (indicating a negative direction), and the Y component is 41 miles. The paragraph also explains that the third vector, D3, has no horizontal component and a vertical component of -47 miles.
📏 Resultant Vector Calculation and Direction
The final paragraph focuses on determining the magnitude and direction of the resultant vector from the sum of the individual displacement vectors. The X and Y components of the resultant vector are calculated by adding the respective components of the three vectors. The magnitude of the resultant vector is found using the Pythagorean theorem, resulting in approximately 55 miles. The direction of the resultant vector with respect to the x-axis is calculated using the tangent function, yielding an angle of 65 degrees.
Mindmap
Keywords
💡Vector
💡Displacement
💡Tail-to-Tip Method
💡Magnitude
💡Direction
💡SoHCaHToA
💡X and Y Components
💡Pythagorean Theorem
💡Resultant Vector
💡Tangent
💡Arctangent
Highlights
A ship makes three displacement vectors in a specific order.
The first vector is 176 miles at 48 degrees north of east.
The second vector is 250 miles at 56 degrees north of west.
The third vector is 30 miles south.
A clear diagram is drawn showing all three displacement vectors.
The vectors are added using the tail-to-tip method.
The resultant vector connects the starting point to the final point of vector 3.
The X and Y components of displacement D1 are calculated using SOHCAHTOA.
D1X is found to be 51 miles and D1Y is 56 miles.
The X and Y components of displacement D2 are also calculated.
D2X is -28 miles (negative x-direction) and D2Y is +41 miles (positive y-direction).
The X and Y components of displacement D3 are determined to be 0 and -47 miles respectively.
The magnitude of the resultant vector is calculated using the Pythagorean theorem.
The resultant magnitude is found to be approximately 55 miles.
The direction of the resultant vector with respect to the x-axis is calculated.
The direction is found to be 65 degrees.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: