AP Physics B Kinematics Presentation #46
TLDRThe video script explains the concept of vector addition using the tail-to-tip method. It illustrates the process of finding the resultant vector of two vectors, A and B, with magnitudes of 8 units (north) and 4.5 units (east), respectively. The script applies the Pythagorean theorem to calculate the magnitude of the resultant vector, C, which is approximately 9.2 units. The explanation is aimed at helping viewers understand the mathematical principles behind vector addition and its practical applications.
Takeaways
- 📚 The script discusses the concept of vector addition and the resultant vector.
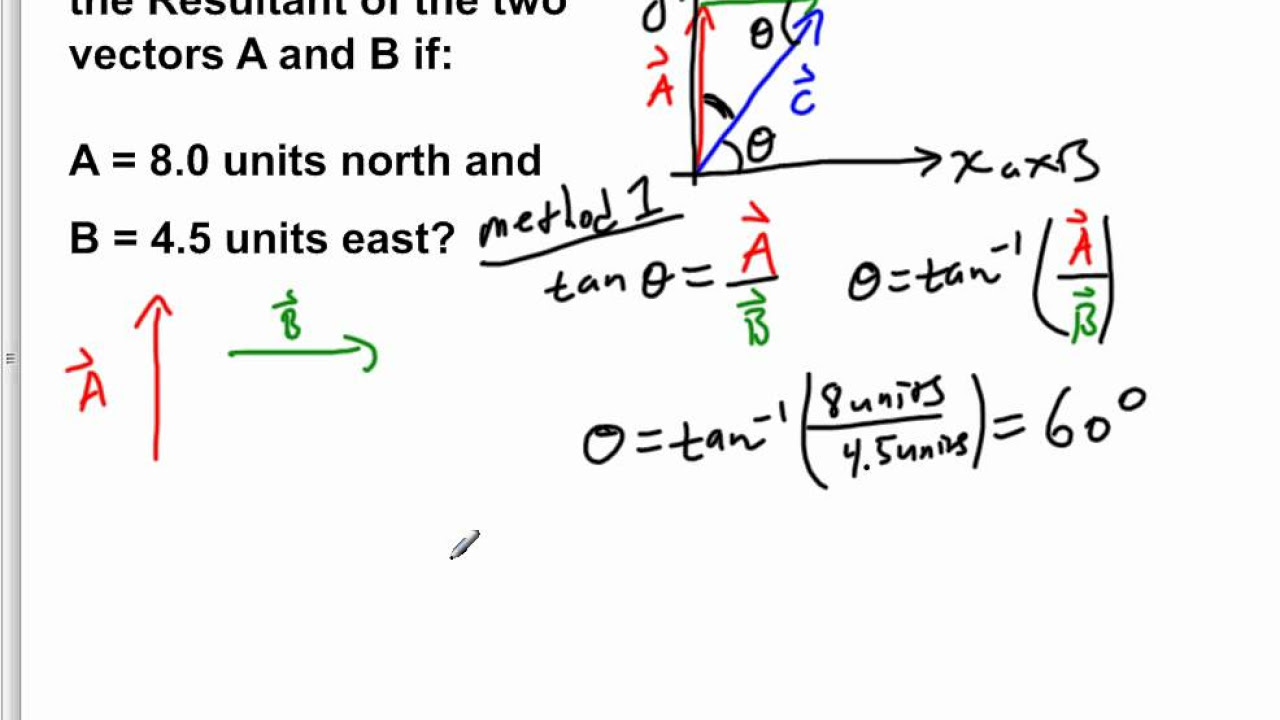
- 🧭 Vector A is described as being 8 units in the North direction.
- 🌐 Vector B is described as being 4.5 units in the East direction.
- 🔍 The script uses the tail-to-tip method to add the vectors together.
- 📐 The Pythagorean theorem is applied to find the magnitude of the resultant vector.
- 🔢 The magnitude of the resultant vector is calculated using the formula \( C = \sqrt{a^2 + b^2} \).
- 📈 The values for a and b are squared and then summed to find the magnitude of the resultant vector.
- 🔢 The calculation results in the square root of 84.2 units squared, which is the magnitude of the resultant vector.
- 📏 The resultant vector is approximately 9.2 units in magnitude.
- 📍 The script uses color coding (green for Vector A, red for Vector B, and blue for the resultant Vector C) to illustrate the vectors.
- 📝 The script emphasizes the importance of understanding direction in vector addition.
Q & A
What are the magnitudes and directions of vectors A and B?
-Vector A has a magnitude of 8 units and is directed north. Vector B has a magnitude of 4.5 units and is directed east.
What notation is used to denote vectors in the script?
-Vectors are denoted using arrows above the letters or by bolding the letters.
What method is used to find the resultant vector of vectors A and B?
-The tail-to-tip method is used to find the resultant vector.
What theorem is applied to calculate the magnitude of the resultant vector?
-The Pythagorean theorem is applied to calculate the magnitude of the resultant vector.
How is the Pythagorean theorem expressed in this context?
-The Pythagorean theorem is expressed as c^2 = a^2 + b^2, where c is the magnitude of the resultant vector, and a and b are the magnitudes of vectors A and B respectively.
What are the values of a^2 and b^2 in this scenario?
-a^2 is 64 (since 8^2 = 64), and b^2 is 20.25 (since 4.5^2 = 20.25).
What is the sum of a^2 and b^2?
-The sum of a^2 and b^2 is 84.25 (64 + 20.25).
How do you find the magnitude of the resultant vector from the sum of a^2 and b^2?
-You take the square root of the sum of a^2 and b^2 to find the magnitude of the resultant vector.
What is the magnitude of the resultant vector C?
-The magnitude of the resultant vector C is approximately 9.2 units.
What is the resultant vector if vector A is 8 units north and vector B is 4.5 units east?
-The resultant vector C, combining vector A and vector B, has a magnitude of approximately 9.2 units.
Outlines
📚 Vector Addition and Resultant Calculation
This paragraph explains the process of finding the magnitude of the resultant vector when two vectors, A and B, are given. Vector A is described as having a magnitude of 8 units to the North, while Vector B has a magnitude of 4.5 units to the East. The method of tail-to-tip vector addition is introduced to combine these vectors. The Pythagorean theorem is then applied to calculate the magnitude of the resultant vector, denoted as C. The calculation involves squaring the magnitudes of A and B, adding them together, and then taking the square root of the sum to find the magnitude of C, which is approximately 9.2 units.
🔍 Resultant Vector Direction and Magnitude
Building upon the previous explanation, this paragraph continues to discuss the resultant vector C, which is the combination of Vector A and Vector B. It clarifies that the resultant vector C, represented in blue, has a magnitude of 9.2 units and is formed by the vector addition of Vector A (8 units North, shown in green) and Vector B (4.5 units East, shown in red). The paragraph reinforces the concept of resultant vector magnitude and direction as derived from the individual vectors' magnitudes and directions.
Mindmap
Keywords
💡Magnitude
💡Vector
💡Resultant
💡Pythagorean Theorem
💡Tail to Tip Method
💡Direction
💡Algebra
💡Hypotenuse
💡Square Root
💡Units
💡North and East
Highlights
Introduction of the problem: finding the magnitude of the resultant of two vectors A and B.
Vector A is defined as 8 units North.
Vector B is defined as 4.5 units East.
Explanation of vector notation using arrows and bold letters.
The concept of adding vectors using the tail-to-tip method.
Application of the Pythagorean theorem to find the resultant vector.
Formulation of the Pythagorean theorem for vector addition: \( c^2 = a^2 + b^2 \).
Substitution of vector magnitudes into the theorem: 8 units and 4.5 units.
Calculation of the squares of the vector magnitudes: 64 and 20.25.
Summation of the squared magnitudes to get 84.2 units squared.
Finding the square root to determine the resultant vector's magnitude.
Resultant vector magnitude is approximately 9.2 units.
Visual representation of the vectors and resultant using different colors.
Explanation of the resultant vector's direction combining North and East.
Emphasis on the practical application of the Pythagorean theorem in vector addition.
Clarification of potential spelling errors and the importance of accurate mathematical communication.
Summary of the process to find the magnitude of the resultant vector.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: