2022 AP Physics 1 Free Response #1
TLDRThe video explains the dynamics of a system involving two blocks connected by a string, with one block on a frictionless surface and attached to a spring. It details the forces acting on the blocks, how block 2 speeds up and slows down, and derives the expression for the displacement before block 2 momentarily comes to rest using energy principles. The importance of changing forces, energy conservation, and the impact of friction on the system's mechanical energy are also discussed.
Takeaways
- 🔧 The video discusses a physics problem involving two blocks connected by a string and a spring, with one block on a frictionless surface and the other on a spring.
- 🎥 The presenter apologizes for a previous video where the microphone was off and promises corrections in the description.
- 📉 Block 2, initially at rest, begins to move downward due to the gravitational force being greater than the tension in the spring.
- 📈 As the spring stretches, the tension force increases, leading to a change in acceleration from downward to upward, causing Block 2 to slow down.
- 🛑 Block 2 comes to a momentary stop when the net force is zero, indicating equilibrium but not the end of motion.
- 📚 The problem cannot be solved using kinematics alone due to the changing force and acceleration, necessitating an energy approach.
- ⚖️ The total mechanical energy of the system remains constant as there are no external forces doing work on the system.
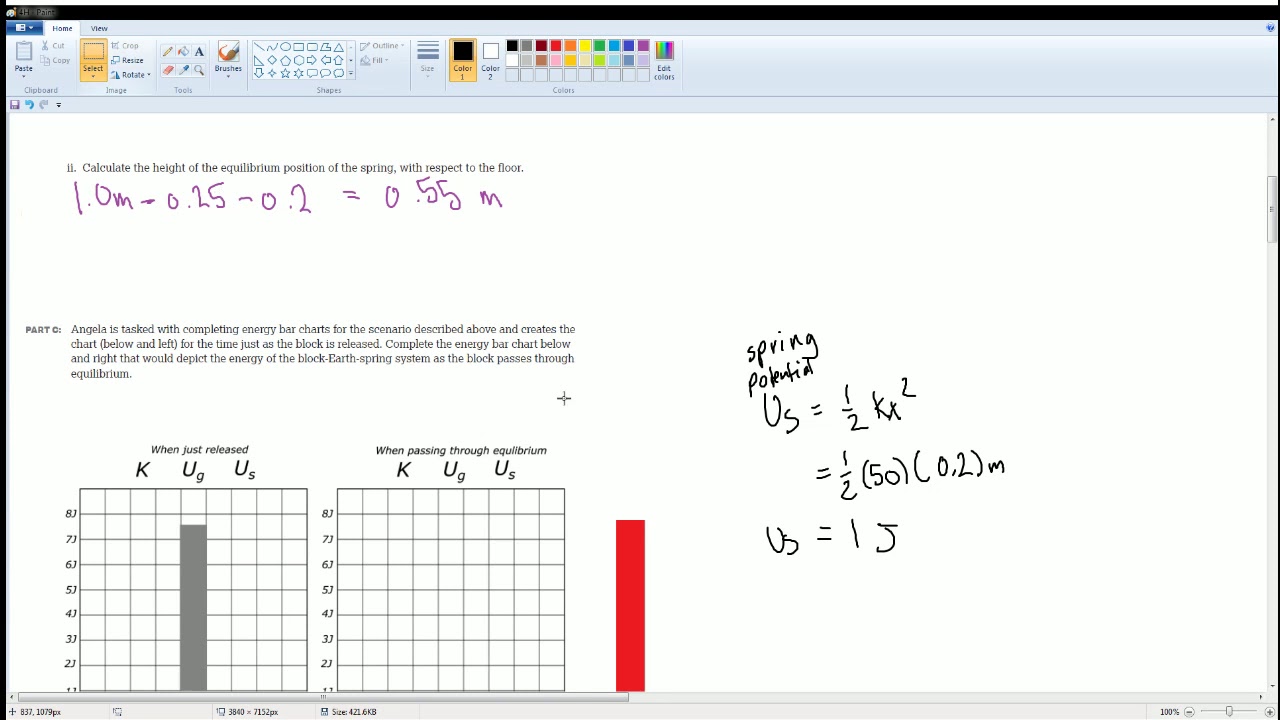
- 🌐 The energy conservation is demonstrated by setting the initial and final states of the system, considering the spring potential energy and gravitational potential energy.
- 📐 The expression for the distance 'delta y' the block travels before momentarily coming to rest is derived using energy principles, resulting in \( ext{delta y} = rac{2m_2g}{k_0} \).
- 🚫 The presence of non-negligible friction would result in energy loss, altering the energy conservation scenario and requiring a different approach.
- 📊 A diagram is suggested to represent the potential and gravitational potential energy changes in the system, with and without friction.
Q & A
What was the issue with the original video?
-The original video had an issue where the microphone was completely shut off by the OBS software, resulting in no audio.
What will be done to address issues or corrections in the video?
-Any issues or corrections will be addressed in the description below the video.
What is the scenario described in the script involving two blocks and a spring?
-The scenario involves two blocks connected by a string. Block one is on a horizontal surface attached to a spring at its unstretched length, with negligible frictional forces. Block two is released from rest and moves downward before momentarily coming to rest.
Why does block two initially speed up after being released?
-Block two initially speeds up because the gravitational force acting on it is greater than the tension in the string, causing a net downward force.
Why does block two eventually slow down and momentarily come to rest?
-Block two slows down and momentarily comes to rest because as the spring stretches, the tension force increases until it matches and then exceeds the gravitational force, causing an upward net force and deceleration.
Why can't kinematics be used to derive the expression for the distance the block travels before momentarily coming to rest?
-Kinematics cannot be used because the force, and thus the acceleration, is changing, which is a requirement for constant acceleration in kinematic equations.
What approach is suggested to derive the expression for the distance the block travels before momentarily coming to rest?
-The energy approach is suggested, considering the conservation of energy among the blocks, spring, and Earth system.
What is the expression derived for the distance 'delta y' the block travels before momentarily coming to rest?
-The expression derived for 'delta y' is delta y = sqrt(2 * m2 * g / k0), where m2 is the mass of block two, g is the acceleration due to gravity, and k0 is the spring constant.
How does the presence of friction affect the energy conservation in the system?
-The presence of friction causes a loss in energy, as some of the mechanical energy is converted into heat due to the work done by friction.
What is the significance of the normal force in the context of work done on the system?
-The normal force is significant because it moves perpendicular to the motion and does not do any work on the system, thus not affecting the total mechanical energy.
How does the script suggest visualizing the energy changes in the system with and without friction?
-The script suggests using a vertical bar chart to represent the potential energy of the spring and the gravitational potential energy of the blocks and Earth system, with shaded bars indicating energy losses due to friction.
Outlines
🔍 Physics Problem Explanation: Block and Spring Dynamics
This paragraph discusses a physics problem involving two blocks connected by a string and a spring. Block one is on a frictionless horizontal surface attached to a spring, while block two is released from rest and moves downward momentarily before coming to rest. The speaker explains why block two initially accelerates due to the gravitational force being greater than the tension force and then decelerates as the spring tension increases. The paragraph concludes with a derivation of the expression for the distance 'delta y' the block travels before coming to rest, emphasizing that this cannot be solved using kinematics due to the changing force and instead requires an energy analysis. The total mechanical energy of the system is shown to remain constant throughout the motion.
📉 Energy Conservation and Friction in a Block-Spring System
The second paragraph expands on the block-spring system by considering the scenario where friction is non-negligible. It explains that the presence of friction leads to a loss in the system's energy. The speaker clarifies that no external forces are doing work on the system, and thus the total mechanical energy should remain constant if there were no friction. However, due to friction, some energy is lost as work. The paragraph includes a discussion on the work done by friction and how it affects the system's energy. It concludes with a visual representation of the energy states of the system in the form of a bar chart, illustrating the potential energy of the spring and the gravitational potential energy of the blocks with and without friction.
Mindmap
Keywords
💡Spring constant
💡Unstretched length
💡Frictional forces
💡Net force
💡Acceleration
💡Gravitational force
💡Tension
💡Potential energy
💡Kinetic energy
💡Mechanical energy
💡Work
Highlights
The video discusses a physics problem involving two blocks connected by a string with one on a horizontal surface and attached to a spring.
Frictional forces are negligible in the system, simplifying the analysis of forces acting on the blocks.
Block 2 is released from rest and initially accelerates downward due to the gravitational force being greater than the tension force.
As the spring stretches, the tension force increases, eventually causing the block to decelerate.
The block momentarily comes to rest when the net force is zero, indicating a balance between gravitational and tension forces.
The problem cannot be solved using kinematics alone due to the changing nature of the forces involved.
An energy-based approach is suggested to solve for the distance the block travels before coming to rest.
The system's total mechanical energy remains constant as there are no external forces doing work on the system.
The potential energy of the spring and the gravitational potential energy of the blocks are considered in the energy conservation equation.
The expression for the distance the block travels before momentarily coming to rest is derived using energy conservation principles.
The derived expression for delta y is \( \frac{2m_2g}{k_0} \), where \( m_2 \) is the mass of block 2, \( g \) is the acceleration due to gravity, and \( k_0 \) is the spring constant.
The importance of considering the system's energy conservation to understand the block's motion is emphasized.
A scenario with non-negligible friction is considered, leading to a loss in the system's energy.
The work done by friction is identified as the cause of energy loss in the system with friction.
A vertical bar chart is used to represent the potential energy of the spring and the gravitational potential energy of the blocks' earth system.
The impact of friction on the system's energy is diagrammed, showing a decrease in potential energy due to work done by friction.
The video concludes by reinforcing the concept that the total mechanical energy of the system does not change in the absence of external work.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: