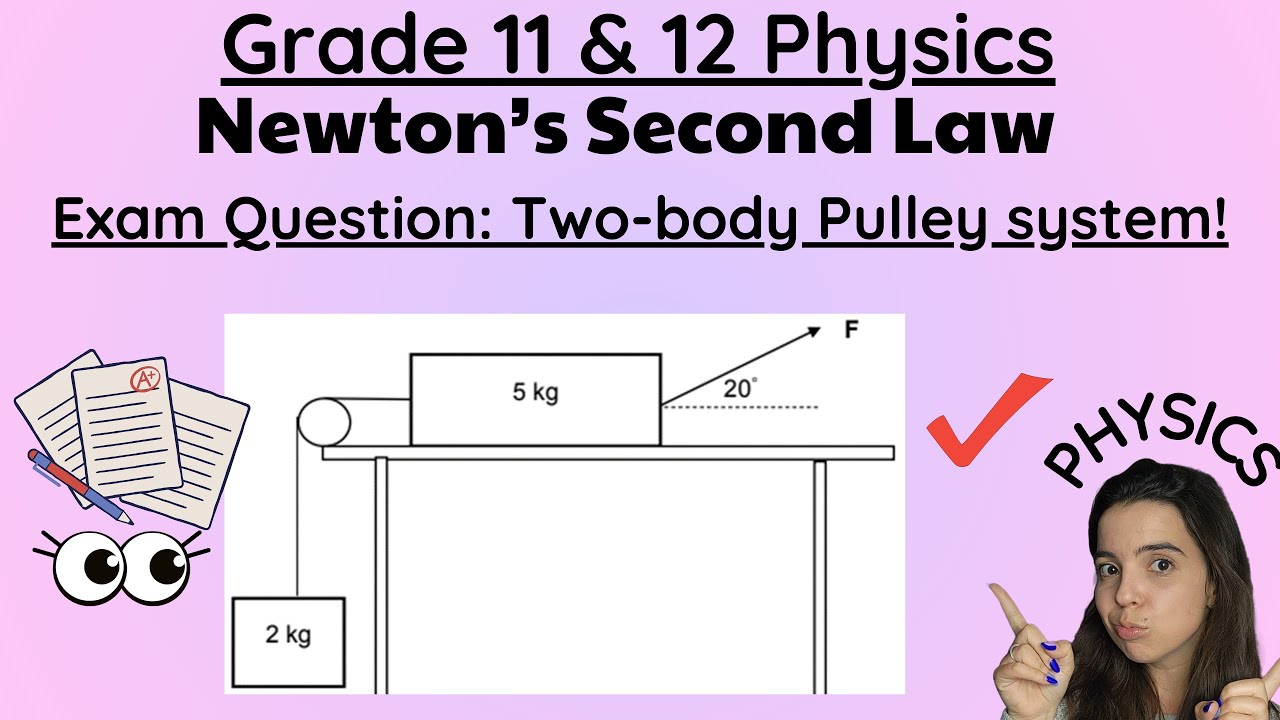
2015 AP Physics 1 free response 1a
TLDRThe video script explains a physics scenario where two blocks of different masses, m1 and m2 (m2 > m1), are connected by a lightweight string over frictionless pulleys. The video discusses the forces acting on the blocks, including gravity and tension, and predicts their motion based on these forces. It is visualized that block 2 will accelerate downwards due to its larger weight, while block 1 will accelerate upwards due to the tension in the string. The script then instructs to draw free-body diagrams to illustrate the forces and their magnitudes, emphasizing that the tension's magnitude must be between the weights of the two blocks to cause the observed accelerations.
Takeaways
- 🔍 The problem involves two blocks connected by a string passing over massless and frictionless pulleys.
- 📈 Block 2 (m2) has a greater mass than Block 1 (m1) and both are released from rest.
- 💡 Intuition suggests that Block 2 will accelerate downwards and Block 1 will accelerate upwards due to the difference in their weights.
- 📚 The force of gravity acting on each block is represented by its mass times the gravitational field (mg).
- 🌐 The weight of Block 2 (m2g) is larger than the weight of Block 1 (m1g) as m2 > m1.
- 🔗 There is an upward tension force in the string that acts on both blocks, with the same magnitude but opposite directions.
- ⚖️ The tension in the string must be greater than m1g to accelerate Block 1 upwards and less than m2g to accelerate Block 2 downwards.
- 📏 The relative lengths of the forces' vectors in the free-body diagrams represent the relative magnitudes of the forces.
- 🎨 The free-body diagrams should accurately depict the forces acting on each block, including both weight and tension forces.
- 📌 The tension force's magnitude is between the weights of the two blocks (m1g < T < m2g).
- 🚀 The net force on Block 1 is upward, leading to its upward acceleration, while the net force on Block 2 is downward, leading to its downward acceleration.
Q & A
What is the main concept discussed in the transcript?
-The main concept discussed in the transcript is the physics of two blocks connected by a string, with one block having a greater mass than the other, and how they interact under the influence of gravity and tension forces.
What are the key elements of the system described in the transcript?
-The key elements of the system are two blocks (m1 and m2), a string of negligible mass, and massless pulleys. The blocks are connected by the string and are subject to gravitational forces and tension forces.
How does the mass of the blocks affect their motion when released from rest?
-The block with the larger mass (m2) will experience a greater gravitational force, causing it to accelerate downwards. Conversely, the block with the smaller mass (m1) will experience a smaller gravitational force and will accelerate upwards due to the tension in the string.
What is the role of the tension force in this system?
-The tension force in the string acts to pull both blocks in the opposite direction of the gravitational force. The magnitude of the tension must be between the weights of the two blocks, causing both blocks to move: the lighter block upwards and the heavier block downwards.
What is the significance of the pulleys being massless and having negligible friction?
-The assumption of massless pulleys with negligible friction simplifies the system by eliminating additional forces that could affect the motion of the blocks. It allows us to focus on the gravitational and tension forces without the complexity of friction and mass of the pulleys.
How does the force of gravity affect the two blocks differently?
-The force of gravity, calculated as mass times the gravitational field (g), affects the blocks differently because of their differing masses. The heavier block (m2) experiences a greater gravitational force than the lighter block (m1), leading to different accelerations when the system is released from rest.
What is the net force acting on each block and what is the resulting motion?
-The net force on block m1 is upwards due to the tension being greater than its weight (m1g), causing it to accelerate upwards. For block m2, the net force is downwards because its weight (m2g) is greater than the tension, causing it to accelerate downwards.
How does the relative magnitude of the forces affect the acceleration of the blocks?
-According to Newton's second law of motion, the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. Therefore, the heavier block (m2) will have a larger acceleration downwards, while the lighter block (m1) will have a smaller acceleration upwards.
What is the significance of drawing free-body diagrams in understanding this system?
-Free-body diagrams are crucial in visualizing and simplifying the complex interactions of forces in a system. They help in identifying all the forces acting on each block, understanding their relative magnitudes, and predicting the motion of the system based on these forces.
How does the molecular or atomic level explanation of tension relate to the macro-level observation?
-At the molecular or atomic level, tension is represented by the forces of covalent bonds pulling on each other throughout the string. On a macro-level, this is observed as a pulling force that acts along the length of the string, influencing the motion of the connected objects.
What is the importance of understanding the relative magnitudes of the forces in the system?
-Understanding the relative magnitudes of the forces is essential for predicting the behavior of the system. It helps in determining the direction and magnitude of the acceleration of the blocks, as well as the overall dynamics of the system under the influence of gravity and tension.
Outlines
📚 Analysis of Block and Pulley System
This paragraph delves into the dynamics of a block and pulley system where two blocks of differing masses, m1 and m2, are connected by a string passing over massless pulleys with negligible friction. The blocks are released from rest, and the voiceover provides an intuitive prediction of the ensuing motion based on the relative weights of the blocks. It is explained that the larger mass (m2) will experience a greater gravitational force, leading to an acceleration downwards, while the smaller mass (m1) will accelerate upwards. The paragraph then instructs on drawing free-body diagrams to illustrate and label the forces acting on each block, emphasizing the relative magnitudes of the forces, particularly the tension in the string and the gravitational forces on both blocks. The tension is described as being greater than m1g but less than m2g, which aligns with the predicted motion of the blocks. The concept of tension is further explained at a molecular level, drawing an analogy to atomic bonds and forces that manifest as macroscopic tension in the string.
🚀 Resultant Forces and Block Acceleration
This paragraph focuses on the resultant forces acting on the blocks and their effects on the blocks' acceleration. It builds on the previous analysis by explaining that block 1 will experience a net upward force, leading to its upward acceleration, while block 2 will have a net downward force, causing it to accelerate downwards. This outcome is consistent with the initial intuitive expectation that the heavier block (m2) would weigh more than the lighter block (m1), thus resulting in different motion patterns for each. The summary reinforces the understanding of how the interplay between gravitational forces and tension in the string dictates the motion of the connected blocks.
Mindmap
Keywords
💡Blocks
💡String
💡Pulleys
💡Gravitational Field
💡Mass
💡Weight
💡Acceleration
💡Tension
💡Free-Body Diagrams
💡Forces
💡Intuition
Highlights
Two blocks are connected by a string of negligible mass over massless pulleys with negligible friction.
The mass m2 of block 2 is greater than the mass m1 of block 1, and the blocks are released from rest.
Block 2, having a larger mass, will experience a larger gravitational force compared to block 1.
The system is set up to allow block 1 to accelerate upwards and block 2 to accelerate downwards with the same magnitude.
The force of gravity on block 1 is represented as m1 times the gravitational field (m1g).
The force of gravity on block 2 is m2 times the gravitational field (m2g) and is larger due to its greater mass.
The tension in the string is an upward force that acts on both blocks and is influenced by the gravitational forces on both sides.
The magnitude of the tension must be larger than m1g to allow block 1 to accelerate upwards.
The magnitude of the tension must be smaller than m2g to allow block 2 to accelerate downwards.
The tension in the string has the same magnitude throughout, reflecting the covalent bonds pulling on each other at an atomic level.
Block 1 experiences a net upward force due to the tension being larger than its weight, resulting in upward acceleration.
Block 2 experiences a net downward force because its weight is greater than the tension, leading to downward acceleration.
The relative lengths of the force vectors in the free-body diagrams represent the relative magnitudes of the forces.
The problem-solving approach begins with intuition based on the physical setup and then proceeds to detailed analysis.
The free-body diagrams are essential for visualizing and calculating the forces acting on each block.
The system demonstrates the principles of Newton's second law of motion, where the net force on an object is equal to the mass of the object multiplied by its acceleration.
The problem illustrates the concept of mechanical advantage through the use of a simple pulley system.
The scenario provides a practical application of understanding the dynamics of connected objects under the influence of gravity.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: