AP Physics Workbook 4.F Energy Transformations
TLDRIn the AP Physics workbook, a scenario is discussed where three blocks are released simultaneously from a height. The debate revolves around the conservation of energy and the resulting speeds and times of the blocks. The key takeaway is that while blocks A and C, which are in freefall, land at the same time and with the same speed due to the conservation of energy, block B, sliding down an incline, will land last due to its longer path and the component of gravitational force acting along the incline. Additionally, the normal force does no work as it is perpendicular to the displacement of the block.
Takeaways
- 📚 The conservation of energy principle is central to understanding the scenario where blocks are released simultaneously and land at the same time.
- 🎯 Block A and Block C, despite starting from the same height, will have different final speeds due to Block C's additional initial kinetic energy from its horizontal launch.
- 🚫 The incorrect assumption by some students that all blocks would have the same final speed because they start with the same gravitational potential energy is disproven by considering the initial mechanical energies of the blocks.
- 🔄 The concept of freefall is applied to Block A and Block C, which both fall vertically and thus reach the ground at the same time, while Block B slides down an inclined plane and takes longer due to the longer path and different acceleration components.
- 📈 The work done by the normal force on Block B is always zero because the force is perpendicular to the displacement vector of the block's motion, similar to the gravitational force on the moon in its orbit around the Earth.
- 🤔 The incorrect equation provided in the script (Work normal = 2π/2 or mg cosine theta) is clarified as not making sense because work only equals zero when the angle theta is 0 degrees, which is not the case for Block B's motion.
- 🌌 The moon's orbit around the Earth serves as an example of work being zero because the moon's displacement is always tangential to the circle, perpendicular to the gravitational force.
- 🧠 The importance of distinguishing between gravitational potential energy (shared by all blocks at the start) and kinetic energy (which varies depending on initial conditions) is highlighted.
- 🔽 Block C's higher total mechanical energy at the start (due to its initial velocity) results in a greater final speed compared to Block A, which starts with only gravitational potential energy.
- 📊 The script emphasizes the need to consider both the vertical and horizontal components of motion when analyzing the work done by forces and the resulting kinematics of objects in different scenarios.
Q & A
What is the main concept being discussed in the transcript?
-The main concept discussed in the transcript is the conservation of energy and its application to different physical scenarios, specifically focusing on the motion of blocks released from rest and blocks launched horizontally, and how their speeds and times of landing are affected.
How does the conservation of energy principle apply to the blocks in the scenario?
-The conservation of energy principle states that the total energy in an isolated system remains constant. In the scenario, all blocks start with the same gravitational potential energy since they are at the same height. As they move, this energy converts into kinetic energy. Despite different paths, the blocks will have the same speed at the bottom if we only consider gravitational potential energy conversion, due to energy conservation.
Why does Carlos disagree with the final speeds of the blocks being the same?
-Carlos disagrees because he considers the initial mechanical energy of the blocks. While Block A and Block B start with only gravitational potential energy, Block C has both gravitational potential energy and kinetic energy due to its initial horizontal velocity. This additional energy means Block C will have a greater speed at the end compared to the other blocks.
What is the significance of Galileo's experiment mentioned in the transcript?
-null
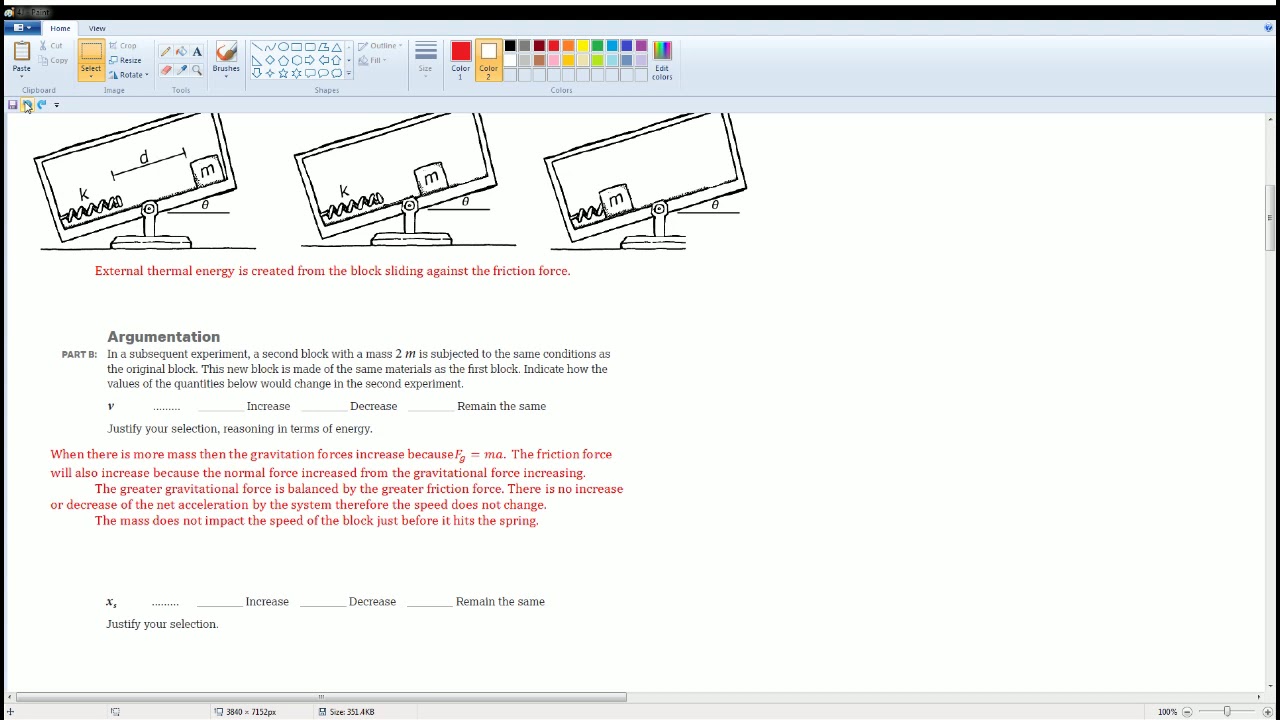
How does the ramp affect Block B's motion and time to reach the bottom?
-The ramp causes Block B to travel a longer distance (the hypotenuse of the right triangle formed by the height and the inclined plane) compared to the vertical freefall of Block A and Block C. Since Block B's path is longer and it only has a component of gravity acting along the ramp, it will take more time to reach the bottom compared to the other blocks.
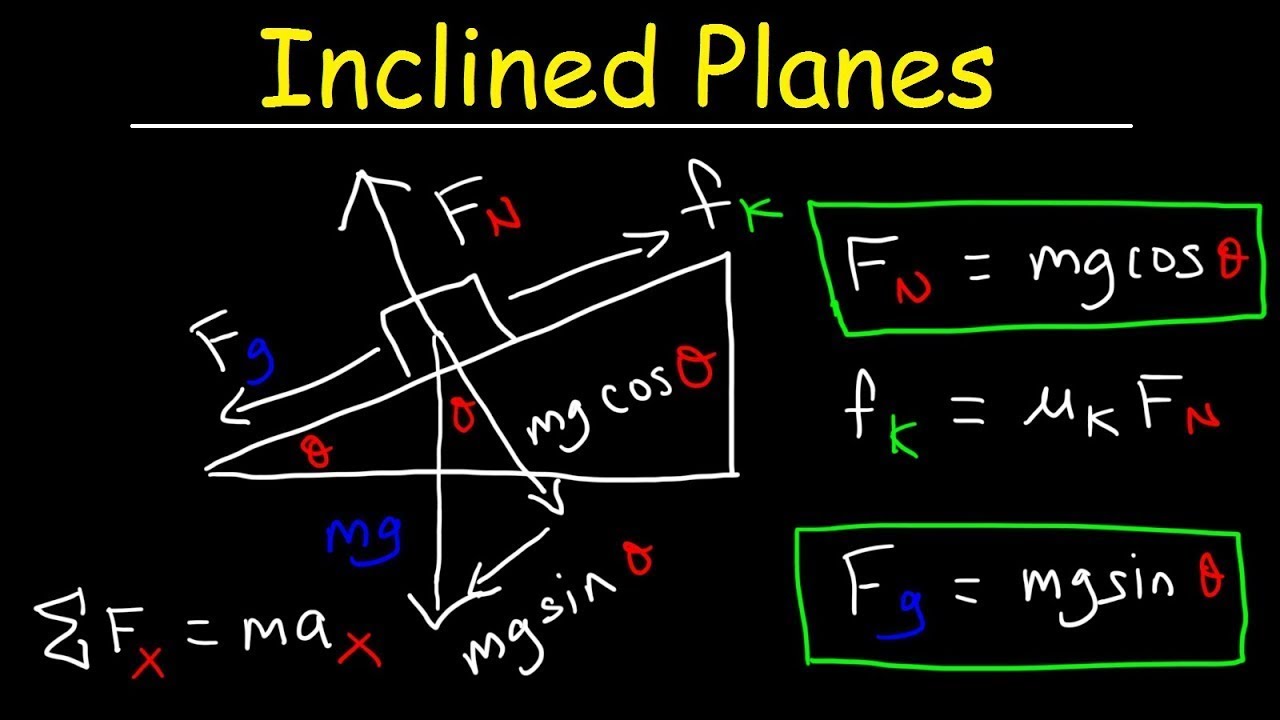
What is the correct component of gravitational force acting on Block B as it slides down the ramp?
-The correct component of gravitational force acting on Block B as it slides down the ramp is the force along the ramp, which is the gravitational force projected onto the ramp's surface. This is given by the equation: F = mg * sine(theta), where mg is the gravitational force, and theta is the angle of the ramp.
Why does the normal force do no work on Block B as it slides down?
-The normal force does no work on Block B because it is always perpendicular to the direction of motion (displacement). Work is calculated as the force applied along the direction of motion times the distance moved, and since the normal force is perpendicular, the cosine of the 90-degree angle between the force and motion is zero, leading to zero work done.
What is the relationship between the work done by forces and the net force in the context of the problem?
-The work done by individual forces can be calculated separately by multiplying each force by the displacement in the direction of the force and the cosine of the angle between them. Alternatively, the net force can be calculated first, and then the work done by this net force can be found using the equation W = F_net * D * cosine(theta), where W is the work, F_net is the net force, D is the displacement, and theta is the angle between the force and displacement.
Why does the equation W = 2 * pi * mg * cosine(theta) / 2 not make sense in the context of the problem?
-The equation W = 2 * pi * mg * cosine(theta) / 2 does not make sense because it incorrectly assumes that the work done by the normal force is zero only when the angle theta equals zero degrees (or 0 radians), which is not true in the context of the problem. The work done by the normal force is always zero because it is perpendicular to the displacement, regardless of the angle.
What is the significance of the moon's orbit in relation to the work done by gravitational force?
-The moon's orbit around the Earth is significant because the gravitational force exerted by the moon on Earth does no work. This is because the moon's displacement at any moment is tangential to its orbit, which is perpendicular to the radial direction of the gravitational force. Since work is calculated as the force along the direction of displacement, and here the angle between the force and displacement is 90 degrees (cosine of 90 degrees is zero), the work done is zero.
Outlines
📚 Physics Concepts: Energy Conservation and Motion
This paragraph introduces the concepts of energy conservation and motion in physics, focusing on the scenario of blocks released from different positions. It discusses the conservation of energy principle, where all blocks have the same initial gravitational potential energy and convert it into kinetic energy. The paragraph corrects misconceptions between two students, Dominic and Carlos, regarding the final speed and time of the blocks. It emphasizes that while blocks A and C will land simultaneously due to freefall, block B will take longer due to its inclined path. The paragraph also references Galileo's experiment on the equivalence of horizontal projection and vertical drop, highlighting the importance of understanding the vertical component of motion.
📐 Analysis of Block Motion: Inclines and Acceleration
The second paragraph delves into the analysis of block motion, particularly focusing on block B sliding down a ramp. It clarifies the incorrect reasoning regarding the time it takes for each block to reach the bottom. The paragraph explains that while blocks A and C are in freefall, block B experiences a different acceleration due to gravity and travels a longer distance along the ramp, resulting in a later arrival at the bottom. It also corrects a mistake made in the force analysis, highlighting the correct component of gravitational force acting on block B. The paragraph concludes with a discussion on the work done by forces, specifically the normal force, which is always perpendicular to the displacement vector of the sliding block, resulting in zero work done.
🌌 Gravitational Work and the Moon's Orbit
The final paragraph explores the concept of work in the context of celestial bodies, using the moon's orbit around the Earth as an example. It addresses a common misconception about the work done by gravitational force on the moon. The paragraph explains that since the moon's displacement is always tangential to its orbit, the gravitational force does no work on the moon because the force is perpendicular to the displacement. This is analogous to the normal force on the sliding block, which also does no work due to its perpendicularity to the displacement. The paragraph reinforces the understanding that work is only done when the force has a component in the direction of motion.
Mindmap
Keywords
💡Work
💡Energy Conservation
💡Gravitational Potential Energy
💡Kinetic Energy
💡Free Fall
💡Inclined Plane
💡Initial Velocity
💡Mechanical Energy
💡Acceleration Due to Gravity (g)
💡Components of Forces
💡Work Done by Forces
Highlights
Introduction to the AP Physics workbook focusing on work and energy concepts.
Discussion on the conservation of energy and its application to blocks released from rest at different heights but landing simultaneously.
Dominik's argument that all blocks land at the same time due to energy conservation.
Carlos's counterargument that block C, with an initial velocity, will have a different speed at the end.
Explanation of Galileo's experiment showing that horizontally projected objects and vertically dropped objects reach the ground at the same time.
Clarification that the vertical motions of objects in free fall are identical, leading to simultaneous landing.
Analysis of the problem involving Ryder, Paw, and Kalenna, and the prediction that Kalenna will reach the bottom first due to the conversion of potential energy to kinetic energy.
Discussion on the conservation of energy and its role in determining that all blocks start with the same gravitational potential energy.
Explanation that block C has a higher total mechanical energy due to its initial kinetic energy from velocity.
Correction of a common misconception that all blocks will have the same final speed, emphasizing that block C will be faster due to its higher mechanical energy.
Discussion on the difference in time it takes for blocks to reach the bottom, with block B taking longer due to its inclined path.
Explanation of the forces acting on block B as it slides down the ramp, including the normal force and gravitational components.
Clarification that the normal force does no work on the block as it is perpendicular to the displacement vector.
Comparison of the block's motion to the moon's orbit around the Earth to explain why no work is done by the gravitational force when the moon's displacement is tangential to the circle.
Incorrect equation analysis and the explanation that work done by the normal force is zero because it is always perpendicular to the displacement.
Final note that work done by the normal force is always zero, analogous to the moon's orbit and the gravitational force.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: