Energy In a Simple Harmonic Oscillator - Maximum Velocity & Acceleration Calculations
TLDRThis educational video script explores the relationship between simple harmonic motion and energy. It begins by calculating the spring constant using Hooke's Law, then determines the amplitude of oscillation. The script proceeds to calculate the maximum acceleration, mechanical energy, and maximum velocity of a 0.5 kg mass attached to a spring. Finally, it demonstrates how to find the velocity at a specific displacement using both the conservation of energy and a derived equation, offering multiple methods to solve physics problems related to harmonic motion.
Takeaways
- 😀 Simple harmonic motion is discussed in relation to energy, involving a force of 300 newtons stretching a spring with a 0.5 kg block attached.
- 🔍 Hooke's Law is used to calculate the spring constant (k), which is the force applied (F) divided by the displacement (x), resulting in k = 1200 N/m.
- 📏 The amplitude of the mass-spring system is the maximum displacement, which in this case is 0.25 meters.
- 🚀 The maximum acceleration is calculated using the formula (a = (k * a) / m), yielding an acceleration of 600 m/s².
- 🔋 The mechanical energy of the system is the sum of kinetic and potential energy, and is calculated to be 37.5 joules.
- 🏁 The maximum velocity of the block is found when it is at the equilibrium position, and is calculated to be 12.25 m/s.
- 🔄 The conservation of mechanical energy principle is applied to understand the relationship between kinetic and potential energy at different positions of the oscillation.
- 📉 At the maximum displacement (amplitude), the potential energy is at its maximum, and the kinetic energy is zero.
- 📈 At the equilibrium position, the kinetic energy is at its maximum, equal to the total mechanical energy of the system.
- 📘 The velocity at any position can be calculated using the formula (v = v_max * sqrt(1 - (x / a)^2)), where v_max is the maximum velocity.
- 🔧 There are multiple methods to solve for velocity, including using the conservation of energy or the specific formula for velocity at a given displacement.
Q & A
What is the formula to calculate the spring constant (k) according to Hooke's Law?
-The spring constant (k) is calculated using the formula k = F / x, where F is the force applied and x is the displacement of the spring.
What is the spring constant for the spring in the video when a force of 300 Newtons stretches it by 0.25 meters?
-The spring constant is 1200 Newtons per meter, calculated by dividing the force of 300 Newtons by the displacement of 0.25 meters.
What is the amplitude of the mass-spring system described in the video?
-The amplitude of the mass-spring system is 0.25 meters, which is the maximum displacement from the equilibrium position when the spring is stretched.
How is the maximum acceleration of the mass in the system calculated?
-The maximum acceleration is calculated by multiplying the spring constant (k) by the amplitude (a) and then dividing by the mass (m) of the system, using the formula a_max = k * a / m.
What is the mechanical energy of the system in the video?
-The mechanical energy of the system is 37.5 Joules, found by using the formula for the total energy of a simple harmonic oscillator, which is E = 0.5 * k * a^2.
How can the maximum velocity of the mass be determined?
-The maximum velocity occurs at the equilibrium position and is determined by the formula v_max = sqrt(k * a / m), where v_max is the maximum velocity, k is the spring constant, a is the amplitude, and m is the mass.
What is the relationship between the maximum velocity and the spring constant, mass, and amplitude?
-The maximum velocity is directly proportional to the square root of the spring constant and amplitude, and inversely proportional to the square root of the mass.
How does the velocity of the mass change when it is not at the equilibrium position?
-The velocity at any position x is given by v = v_max * sqrt(1 - (x^2 / a^2)), where v_max is the maximum velocity and a is the amplitude.
What is the velocity of the mass when it is at a displacement of 0.15 meters from the equilibrium position?
-The velocity at a displacement of 0.15 meters is 9.8 meters per second, calculated using the conservation of energy or the specific formula for velocity at a given displacement.
How does the conservation of energy principle apply to the mass-spring system in the video?
-The conservation of energy principle states that the total mechanical energy of the system remains constant. At the equilibrium position, this energy is entirely kinetic, and at the maximum displacement, it is entirely potential.
What happens to the kinetic and potential energies of the system at the equilibrium position and at the maximum displacement?
-At the equilibrium position, all the mechanical energy is kinetic because the potential energy is zero. At the maximum displacement, all the mechanical energy is potential because the kinetic energy is zero.
Outlines
🔍 Introduction to Simple Harmonic Motion Problem
This paragraph introduces a physics problem involving simple harmonic motion and energy. A force of 300 newtons is used to stretch a spring with a 0.5 kg block attached, displacing it by 0.25 meters. Upon release, the block performs simple harmonic motion. The task is to calculate various properties of the system, including the spring constant, amplitude, maximum acceleration, mechanical energy, maximum velocity, and velocity at a specific displacement. The explanation begins with Hooke's Law to determine the spring constant, which is calculated as 1200 N/m by dividing the applied force by the displacement.
📏 Calculating Amplitude and Maximum Acceleration
The second paragraph delves into calculating the amplitude of the mass-spring system, which is the maximum displacement and in this case is 0.25 meters. It also explains how to calculate the maximum acceleration using the spring constant, amplitude, and mass, resulting in an acceleration of 600 m/s². The paragraph emphasizes the relationship between the applied force, mass, and acceleration, and how these quantities can be used interchangeably to find the acceleration in the context of simple harmonic motion.
🔄 Mechanical Energy and Maximum Velocity
This paragraph discusses the concept of mechanical energy in the system, which is the sum of kinetic and potential energy. The formula for mechanical energy is presented, and by substituting the known values, the energy is calculated to be 37.5 joules. The paragraph then explains the relationship between maximum velocity, spring constant, mass, and amplitude, and provides a formula to calculate the maximum velocity, which is found to be 12.25 m/s. The explanation highlights the conservation of mechanical energy and how it transitions between kinetic and potential energy at different positions in the oscillation cycle.
📉 Velocity at a Specific Displacement
The final paragraph focuses on finding the velocity of the block at a displacement of 0.15 meters from the equilibrium position. It presents two methods to calculate this: one using the conservation of energy principle and the other using a specific formula that relates velocity to the maximum velocity, displacement, and amplitude. Both methods yield a velocity of 9.8 m/s at the given displacement. The paragraph reinforces the idea that the mechanical energy remains constant throughout the motion, and the kinetic and potential energies vary inversely with respect to each other.
Mindmap
Keywords
💡Simple Harmonic Motion
💡Force
💡Spring Constant
💡Amplitude
💡Acceleration
💡Mechanical Energy
💡Maximum Velocity
💡Velocity
💡Conservation of Energy
💡Displacement
Highlights
The video focuses on solving a problem involving simple harmonic motion and energy.
A force of 300 newtons is used to stretch a spring with a 0.5 kg block by 0.25 meters.
The block is released from rest and undergoes simple harmonic motion.
The task is to calculate the spring constant, amplitude, maximum acceleration, mechanical energy, maximum velocity, and velocity at x=0.15.
The spring constant k is calculated using Hooke's Law, F/x, resulting in 1200 N/m.
The amplitude of the mass-spring system is the maximum displacement, which is 0.25 meters.
Maximum acceleration is calculated as the spring constant times amplitude divided by mass, yielding 600 m/s².
Mechanical energy of the system is the sum of kinetic and potential energy, calculated to be 37.5 joules.
The maximum velocity is found using the relationship between mechanical energy and kinetic energy, resulting in 12.25 m/s.
The maximum velocity occurs at the equilibrium position where potential energy is zero.
A simple equation for maximum velocity is provided: √(k/m) * amplitude.
The velocity at any position is calculated using the equation v_max * (1 - x²/a²)^0.5.
The velocity at x=0.15 meters is found to be 9.8 m/s using the conservation of energy principle.
The problem-solving process demonstrates the application of Hooke's Law, Newton's second law, and energy conservation in simple harmonic motion.
The video provides multiple methods for calculating velocities, emphasizing the importance of understanding energy transformations.
The importance of distinguishing between kinetic and potential energy at different positions in the oscillation cycle is highlighted.
Transcripts
Browse More Related Video
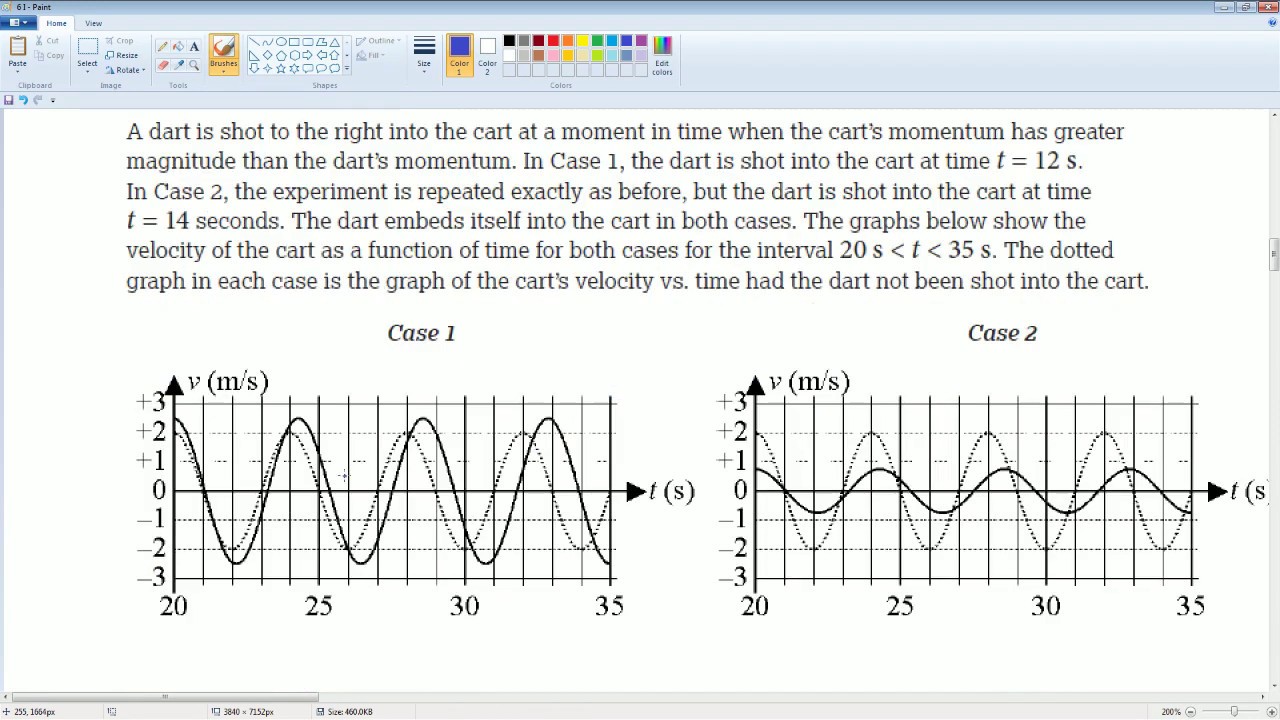
AP Physics Workbook 6.I Changing Mass and Period of a Mass Spring SYstem

AP Physics B - 2013 #2 (Springs)

Simple Harmonic Motion - Complete Review of the Mass-Spring System
AP Physics Lecture on Simple Harmonic Motion. Watch this before 6.C
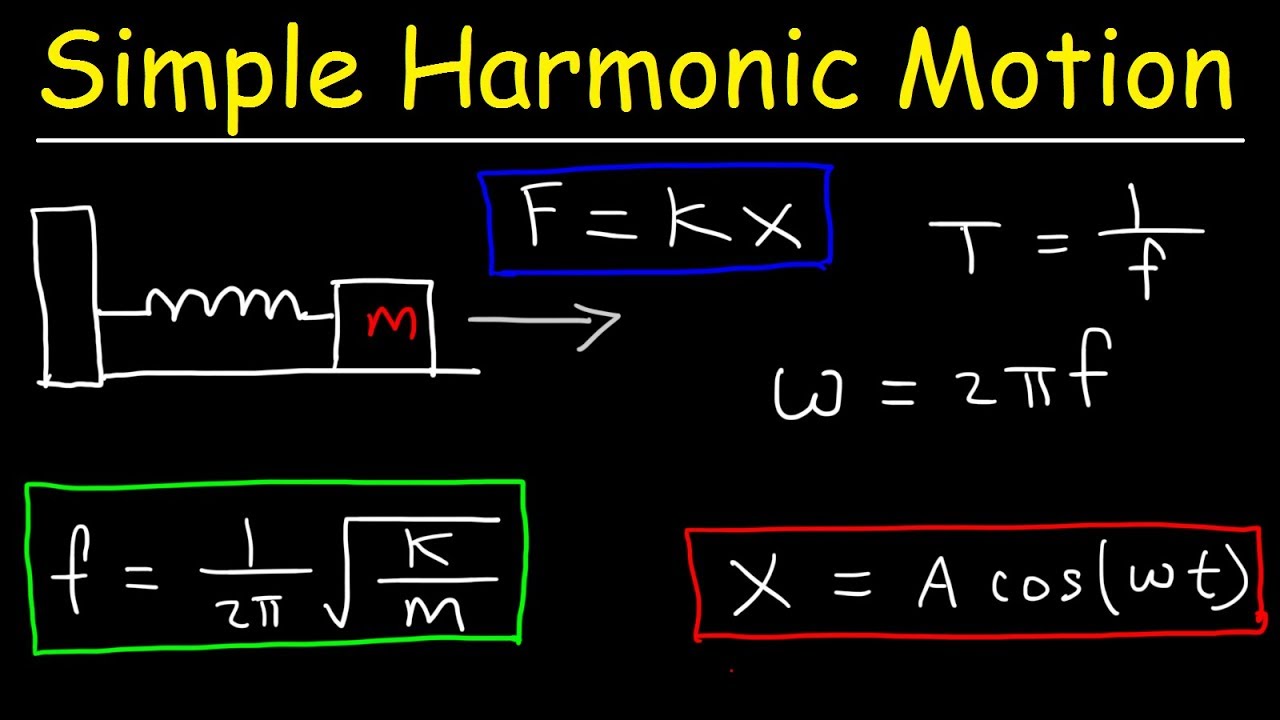
How To Solve Simple Harmonic Motion Problems In Physics
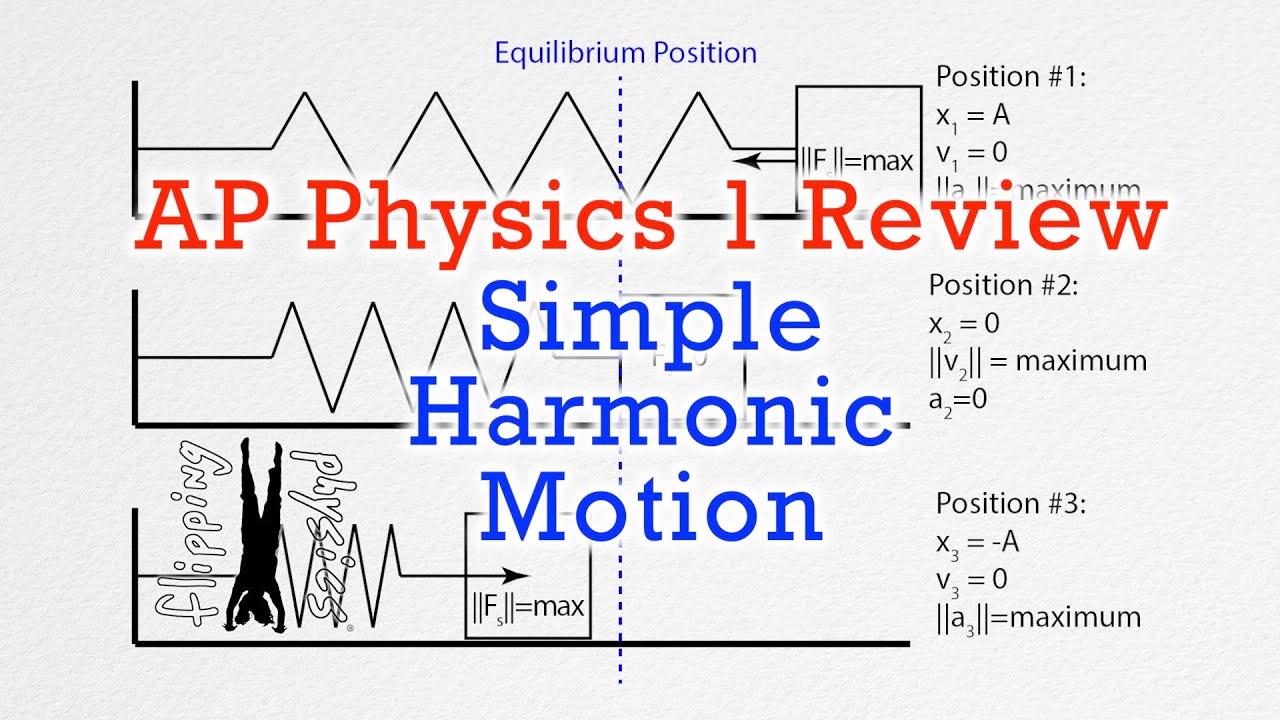
AP Physics 1: Simple Harmonic Motion Review
5.0 / 5 (0 votes)
Thanks for rating: