AP Physics Lecture on Simple Harmonic Motion. Watch this before 6.C
TLDRThis lecture introduces simple harmonic motion (SHM) using a tutorial approach, focusing on the motion of an orange ball attached to a spring. The ball undergoes oscillation, tracing a circular path, and its motion is described by a cosine function with a period defined as 2π/ω. The lecture explains how the angular velocity and acceleration are related to the spring constant and mass, and how the position, velocity, and acceleration graphs are interconnected. The key takeaway is understanding the principles of SHM, derived from Hooke's law and Newton's second law.
Takeaways
- 📌 Simple harmonic motion is a type of periodic motion where an object moves back and forth around an equilibrium position.
- 🔴 The motion is described by a sine function for position (x = A cos(ωt)), where A is the amplitude and ω is the angular frequency.
- 📈 The period (T) of the motion, which is the time taken for one complete cycle, is given by T = 2π/ω.
- 📊 The angular frequency (ω) depends on the spring constant (k) and the mass (m) of the object, with the relationship ω = √(k/m).
- 🏋️♂️ The force exerted by the spring on the object is proportional to the displacement (F = -kx), following Hooke's Law, and is directed towards the equilibrium position.
- 🔄 The motion can be visualized as a circle, with the object tracing out a half-circle from maximum compression to maximum extension and back.
- 📉 The velocity of the object in simple harmonic motion follows a sine function (v = -ωA sin(ωt)), and is at maximum at the equilibrium position and zero at the points of maximum displacement.
- 🚫 The acceleration of the object is always directed towards the equilibrium position, with the magnitude given by a = -ω^2x, and is at maximum at the maximum displacement points.
- 🔄 The relationship between position, velocity, and acceleration in simple harmonic motion is such that the slope of the position graph at any point equals the velocity at that point, and the slope of the velocity graph equals the acceleration at that point.
- 🔎 The characteristics of simple harmonic motion can be derived from Newton's second law when applied to the force exerted by the spring.
Q & A
What is simple harmonic motion?
-Simple harmonic motion is a type of periodic motion where an object moves back and forth along a straight line, experiencing a restoring force that is proportional to the displacement and in the opposite direction. It is exemplified by the motion of a ball attached to a spring.
How is the positive direction defined in the context of the lecture?
-In the lecture, the positive direction is defined as the rightward direction, where the ball initially has a positive displacement to the right.
What are the key characteristics of the position versus time graph for simple harmonic motion?
-The position versus time graph for simple harmonic motion is a cosine wave. It starts at the amplitude or maximum displacement, goes through equilibrium (the trough when fully compressed), and completes a full cycle back to its initial position, representing one period of motion.
What is the mathematical expression for the position of the wave in simple harmonic motion?
-The position of the wave in simple harmonic motion is given by the equation x = A cos(Ωt), where A is the amplitude, Ω is the angular frequency, and t is time.
How does the period of simple harmonic motion relate to angular frequency?
-The period T of simple harmonic motion is the time taken for one complete cycle of the motion and is related to the angular frequency Ω by the equation T = 2π/Ω.
What happens to the period when the angular velocity is increased?
-When the angular velocity is increased, the period of the motion decreases, meaning the ball completes its oscillation in a shorter amount of time.
What is the equation for velocity in simple harmonic motion?
-The velocity v in simple harmonic motion can be described by the equation v = -ΩA sin(Ωt), where Ω is the angular frequency and t is time.
How is acceleration related to the position in simple harmonic motion?
-The acceleration a in simple harmonic motion is given by the equation a = -Ω^2 x, where Ω is the angular frequency and x is the position. It always points inwards, representing centripetal acceleration.
How are position, velocity, and acceleration related to each other in simple harmonic motion?
-In simple harmonic motion, the slope of the position graph at any point equals the velocity at that point, and the slope of the velocity graph equals the acceleration at that point. These relationships can be derived using calculus and the principles of differentiation.
What are the two key equations derived from Newton's second law for simple harmonic motion?
-Using Newton's second law, the angular acceleration α can be found using the equation α = K/m, where K is the spring constant and m is the mass. The period T of the motion is given by T = 2π√(m/K).
How does Hooke's law relate to simple harmonic motion?
-Hooke's law states that the force exerted by a spring is proportional to the displacement from its equilibrium position and is directed opposite to the displacement. This principle is the foundation for understanding the restoring force in simple harmonic motion and leads to the mathematical descriptions of the motion.
Outlines
📚 Introduction to Simple Harmonic Motion
The first paragraph introduces the concept of simple harmonic motion using the example of an orange ball attached to a spring. The ball is initially displaced to the right and undergoes oscillation, demonstrating the harmonic motion. The direction of displacement is defined as positive, and the ball experiences an initial acceleration to the left. The motion is described as a full oscillation, tracing a circular path. The key points include the initial positive displacement, the force of the spring causing acceleration, and the full circular motion representing one complete oscillation. The position versus time graph of the motion is also discussed, highlighting the amplitude, equilibrium points, and the period of oscillation. The amplitude is described as the maximum displacement, and the period is defined as the time taken for one complete cycle of the wave. The relationship between angular velocity and period is also explained, noting that an increase in angular velocity results in a quicker completion of the cycle.
📐 Mathematical Analysis of Simple Harmonic Motion
The second paragraph delves into the mathematical analysis of simple harmonic motion. It discusses the relationship between position, velocity, and acceleration using calculus, highlighting that the slope of the position graph at any point equals the velocity at that point, and the slope of the velocity graph equals the acceleration at that point. The equations for simple harmonic motion, angular acceleration, and angular velocity are derived using Newton's second law. The period of the motion is shown to depend only on the mass and the spring constant, with the formula for the period given as T = 2π/Ω. The angular velocity is determined to depend solely on the spring constant and mass. The paragraph concludes by emphasizing that understanding simple harmonic motion starts with Hooke's law, and all other aspects of the motion follow from there.
Mindmap
Keywords
💡Simple Harmonic Motion
💡Positive Direction
💡Displacement
💡Spring Force
💡Oscillation
💡Angular Velocity
💡Acceleration
💡Period
💡Amplitude
💡Hooke's Law
💡Centripetal Acceleration
Highlights
Simple harmonic motion is described as a ball oscillating due to being attached to a spring.
The ball undergoes a full oscillation due to the harmonic motion.
The direction of the initial displacement of the ball is defined as positive.
The ball experiences an initial acceleration to the left due to the spring force.
Simple harmonic motion can be visually represented as a full circular motion.
The ball is fully stretched when the angle equals zero.
At an angle of pi/2 or 90 degrees, the ball is at equilibrium.
The ball is fully compressed when the angle is pi or 180 degrees.
The position versus time graph of simple harmonic motion shows a complete wave cycle.
The position of the wave can be defined as the amplitude times cosine of Omega times T.
The period T is defined as 2 PI over Omega.
An increase in angular velocity results in a quicker completion of the cycle.
The velocity of the ball follows a negative 8 Omega sine Omega T equation.
The acceleration graph shows an inward pointing graph due to centripetal acceleration.
The position, velocity, and acceleration are related by the first derivative.
Shifting the position graph by 90 degrees to the left yields the velocity graph.
Further shifting the velocity graph by 90 degrees to the left results in the acceleration graph.
Simple harmonic motion is derived from Hooke's law and can be further analyzed using Newton's second law.
The angular acceleration formula is derived from setting Newton's second law equal to the spring force.
The period of the motion depends only on the mass and the spring constant.
Transcripts
Browse More Related Video

Simple Harmonic Motion - Complete Review of the Mass-Spring System
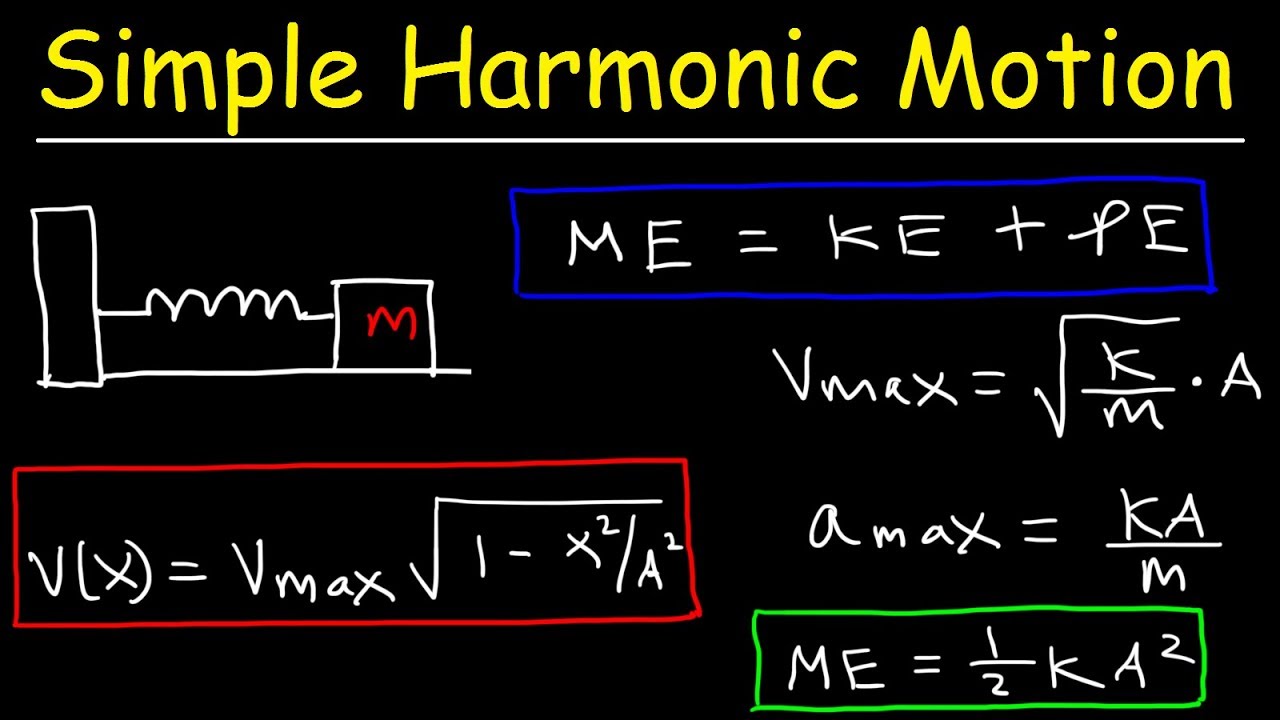
Energy In a Simple Harmonic Oscillator - Maximum Velocity & Acceleration Calculations

AP Physics 1 - Simple Harmonic Motion

Simple harmonic motion and angular frequency [IB Physics SL/HL]
AP Physics Workbook 6.F Determining If Motion is SHM

01 - Oscillations And Simple Harmonic Motion, Part 1 (Physics Tutor)
5.0 / 5 (0 votes)
Thanks for rating: