How To Solve Simple Harmonic Motion Problems In Physics

The Organic Chemistry Tutor
17 Nov 201714:10
EducationalLearning
32 Likes 10 Comments

TLDRThis video script offers a comprehensive guide to solving basic simple harmonic motion problems in physics. It covers the calculation of period, frequency, and angular frequency for a spring-mass system, using Hooke's Law and the formula for simple harmonic motion. The script provides step-by-step solutions for determining the spring constant, frequency of vibration, and other parameters from given data. It also explains the relationship between the spring constant and the frequency of oscillation, and how to derive formulas for these calculations. The video is an excellent resource for anyone looking to understand and apply the principles of simple harmonic motion.

Takeaways
  • πŸ“ The period of a simple harmonic oscillator can be calculated using the formula T = 2Ο€βˆš(m/k), where m is the mass and k is the spring constant.
  • πŸ”Š Frequency (f) is the inverse of the period (T), calculated as f = 1/T.
  • πŸŒ€ Angular frequency (Ο‰) is related to frequency by the formula Ο‰ = 2Ο€f, and it represents the rate of rotation in radians per second.
  • πŸ“ˆ To find the spring constant (k) when a force (F) is applied and causes a displacement (x), use Hooke's Law: F = kx.
  • πŸ”„ When the spring constant is doubled, the frequency of the oscillator increases by a factor of √2.
  • πŸ“Š The position of an oscillator is described by the equation x = A cos(Ο‰t), where A is the amplitude and Ο‰ is the angular frequency.
  • πŸ‹οΈβ€β™‚οΈ Amplitude is the maximum displacement of the oscillator from its equilibrium position.
  • πŸ”’ The spring constant can be calculated from the frequency and mass using the formula k = mω².
  • πŸ•°οΈ The period can be found by inverting the frequency, using the formula T = 1/f.
  • πŸ”§ Understanding and applying these formulas is essential for solving basic simple harmonic motion problems in physics.
Q & A

  • What is the formula to calculate the period of a simple harmonic oscillator?

    -The period of a simple harmonic oscillator can be calculated using the formula T = 2Ο€ * sqrt(m/k), where m is the mass of the oscillator and k is the spring constant.

  • How do you find the frequency of a simple harmonic oscillator?

    -The frequency (f) of a simple harmonic oscillator is found by taking the reciprocal of the period (T), so f = 1/T.

  • What is the angular frequency in the context of simple harmonic motion?

    -The angular frequency (Ο‰) is related to the frequency (f) by the equation Ο‰ = 2Ο€f. It represents the rate of change of the angle in radians per second for the oscillator.

  • How can you calculate the spring constant if you know the force applied and the extension or compression of the spring?

    -The spring constant (k) can be calculated using Hooke's Law, which states that the force (F) is equal to the spring constant (k) times the displacement (x), or F = kx. Therefore, k = F/x.

  • How does the spring constant affect the frequency of a simple harmonic oscillator?

    -The frequency of a simple harmonic oscillator is directly proportional to the square root of the spring constant. As the spring constant increases, the frequency increases, and vice versa.

  • What is the relationship between the frequencies of two springs with different spring constants?

    -The ratio of the frequencies of two springs is equal to the square root of the ratio of their spring constants. This can be expressed as f2/f1 = sqrt(k2/k1).

  • How can you determine the amplitude of a simple harmonic oscillator from its displacement equation?

    -The amplitude is the maximum displacement of the oscillator, which is the coefficient in front of the cosine function in the displacement equation x = A * cos(Ο‰t), where A is the amplitude.

  • What is the relationship between angular frequency and frequency?

    -The angular frequency (Ο‰) is related to the linear frequency (f) by the equation Ο‰ = 2Ο€f. This means that the angular frequency is the frequency multiplied by 2Ο€.

  • How can you calculate the period of a simple harmonic oscillator if you know the frequency?

    -The period (T) of a simple harmonic oscillator can be found by taking the reciprocal of the frequency (f), so T = 1/f.

  • What formula can be used to calculate the spring constant from the mass and frequency of an oscillator?

    -The spring constant (k) can be calculated using the formula k = m * Ο‰^2, where m is the mass of the oscillator and Ο‰ is the angular frequency.

  • How does the mass of an oscillator affect its frequency and period?

    -The frequency and period of an oscillator are inversely related to the square root of its mass. As the mass increases, the frequency decreases and the period increases, and vice versa.

Outlines
00:00
πŸ“ Simple Harmonic Motion: Period, Frequency, and Angular Frequency Calculation

This paragraph introduces the concept of simple harmonic motion in physics and explains how to calculate the period, frequency, and angular frequency of an oscillator. It uses a specific problem involving a horizontal spring with a 0.75 kg mass to demonstrate the calculations. The period is determined using the formula involving mass and spring constant, leading to a period of 0.314 seconds. The frequency is then found by taking the reciprocal of the period, resulting in 3.183 Hz. Lastly, the angular frequency is calculated using the frequency value, resulting in approximately 20 radians per second. The explanation is clear and methodical, providing a solid foundation for understanding these fundamental concepts in simple harmonic motion.

05:01
πŸ”© Spring Constant Calculation and Frequency Relation

This paragraph delves into the calculation of the spring constant using Hooke's Law and the relationship between spring constant and the frequency of oscillation. It presents a scenario where a 0.5 kg mass is attached to a spring and stretched by a 500 N force by 0.35 meters. The spring constant is calculated by dividing the force by the displacement, yielding 14.28 N/m. The frequency of the oscillator is then found using the spring constant and mass, resulting in 8.51 Hz. The paragraph further explains how the frequency changes with an increase in the spring constant, demonstrating that a quadrupling of the spring constant leads to a doubling of the frequency. A formula is derived to relate the frequencies and spring constants of two different oscillators, and an example calculation confirms this relationship.

10:01
πŸŒ€ Oscillation Equation Analysis and Amplitude Determination

This paragraph focuses on analyzing an oscillation equation and determining the amplitude, frequency, period, and spring constant of an oscillator. The equation x = 0.65 cosine(7.35t) is given, and the amplitude is identified as the maximum displacement, which is 0.65 in this case. The angular frequency is derived from the coefficient of 't' in the cosine function, which is 7.35 radians per second. Using the angular frequency, the frequency is calculated to be 1.17 Hz, and the period is found to be 0.855 seconds. Finally, the spring constant is calculated using the mass and frequency, following the formula involving the square of the angular frequency, resulting in a spring constant of 40.5 N/m. The explanation is thorough, providing a step-by-step guide to understanding and solving problems involving oscillation equations.

Mindmap
Keywords
πŸ’‘Simple Harmonic Motion
Simple Harmonic Motion (SHM) is a type of periodic motion where an object moves back and forth along a straight line or an arc, experiencing a restoring force that is directly proportional to the displacement and in the opposite direction. In the context of the video, SHM is the central theme, as it is applied to a spring-mass system to explain various physical quantities such as period, frequency, and angular frequency. The video uses the formula for SHM to solve problems involving the motion of a mass attached to a spring.
πŸ’‘Period
The period of a motion is the time taken for one complete cycle of the motion. In the context of the video, the period of a spring-mass system undergoing SHM is calculated using the formula T = 2Ο€βˆš(m/k), where m is the mass of the object and k is the spring constant. The period is a key parameter in understanding the temporal aspects of SHM and is used to determine other quantities like frequency and angular frequency.
πŸ’‘Frequency
Frequency is the number of cycles of a motion that occur in a unit of time, typically measured in Hertz (Hz). In the context of SHM, frequency is the inverse of the period (f = 1/T). It describes how often the oscillation repeats and is directly related to the rate at which the system moves through its cycle. The video demonstrates how to calculate the frequency of a spring-mass system from its period.
πŸ’‘Angular Frequency
Angular frequency, denoted by the symbol Ο‰, is the rate of change of the angle in radians per unit of time for periodic motion. In SHM, it is related to the linear frequency (f) by the factor of 2Ο€ (Ο‰ = 2Ο€f). Angular frequency is important in the analysis of SHM because it allows for the use of trigonometric functions to describe the motion. The video shows how to calculate the angular frequency from the linear frequency for a given system.
πŸ’‘Spring Constant
The spring constant, denoted by k, is a measure of the stiffness of a spring. It is defined by Hooke's Law as the ratio of the force applied to the spring to the displacement caused by that force (F = kx). In the context of SHM, the spring constant is a critical parameter that, along with the mass of the attached object, determines the period and frequency of the oscillation. The video explains how to calculate the spring constant from given force and displacement values.
πŸ’‘Hooke's Law
Hooke's Law is a fundamental principle in physics that states that the force (F) needed to extend or compress a spring by some distance (x) is proportional to that distance, and always acts in the opposite direction of the displacement. The proportionality constant is the spring constant (k), making the relationship F = kx. This law is essential for understanding the behavior of springs in SHM and is used to calculate the spring constant in the video.
πŸ’‘Amplitude
Amplitude is the maximum displacement of a point in a periodic motion from its equilibrium position. In the context of SHM, it represents the extent of the oscillation, indicating the furthest point the mass will move away from its rest position. The amplitude is a crucial parameter in describing the energy and intensity of the motion, and it is directly visible in the position-time graph of SHM as the peak value of the wave.
πŸ’‘Equilibrium Position
The equilibrium position is the position of rest or balance in a physical system where the net external force is zero. In the context of a spring-mass system undergoing SHM, it is the position where the spring has no deformation, and the mass is neither being stretched nor compressed. All motions of the mass are relative to this equilibrium position, and it serves as the reference point for describing the oscillation.
πŸ’‘Cosine Function
The cosine function is a trigonometric function that describes periodic fluctuations or oscillations of a quantity. In the context of SHM, the cosine function is used to express the position of the mass as a function of time, with the amplitude being the maximum value of the oscillation and the angular frequency determining the rate at which the oscillation occurs. The cosine function allows for a precise mathematical description of the oscillator's motion over time.
πŸ’‘Radian
A radian is a unit of angular measure used in mathematics and physics, equivalent to the angle subtended at the center of a circle by an arc whose length is equal to the radius of the circle. In the context of the video, radians are used to express angular frequency, which is the rate of change of angle in radians per unit of time for periodic motion like SHM. The use of radians allows for a consistent and universal description of angular motion.
πŸ’‘Formula Derivation
Formula derivation is the process of obtaining a mathematical relationship or equation through logical steps and reasoning. In the context of the video, formula derivation is used to establish the relationships between different parameters of a spring-mass system, such as the period, frequency, angular frequency, and spring constant. The video demonstrates how to derive formulas for SHM and use them to solve physical problems.
Highlights

The video discusses solving basic simple harmonic motion problems in physics.

The first problem involves a horizontal spring with a mass of 0.75 kg undergoing simple harmonic motion.

The period, frequency, and angular frequency of the oscillator are to be calculated.

The formula for calculating the period of an oscillator is provided, which is 2Ο€ times the square root of mass divided by spring constant.

The mass and spring constant given for the first problem are 0.75 kg and 300 N/m respectively.

The period of the first oscillator is calculated to be 0.314 seconds.

The frequency is found by taking the reciprocal of the period and is calculated to be 3.183 Hz.

The angular frequency is calculated as 2Ο€ times the frequency, resulting in approximately 20 radians per second.

The second problem involves a force of 500 N stretching a spring with a 0.5 kg mass by 0.35 meters.

The spring constant is calculated using Hooke's Law, which is the force divided by the change in length, resulting in 14.28 N/m.

The frequency of the second oscillator is calculated to be 8.51 Hz.

The third problem examines the change in frequency when the spring constant is increased from 100 N/m to 400 N/m.

The frequency of a spring is proportional to the square root of the spring constant.

The new frequency is calculated to be 50 Hz when the spring constant is increased by a factor of four.

A formula is provided to relate frequency to the spring constant, showing that the new frequency is the square root of the new spring constant divided by the old spring constant.

The final problem involves a 0.75 kg mass vibrating according to a cosine function to determine amplitude, frequency, period, and spring constant.

The amplitude is identified as the maximum displacement, which is 0.65 in the given equation.

The angular frequency is given as 7.35 rad/s, which allows for the calculation of the frequency, which is 1.17 Hz.

The period is calculated as 0.855 seconds by taking the reciprocal of the frequency.

The spring constant is determined to be 40.5 N/m using the mass and angular frequency.

The video concludes by emphasizing the importance of understanding the formulas for solving simple harmonic motion problems.

Transcripts

Browse More Related Video

Simple Harmonic Motion - Complete Review of the Mass-Spring System

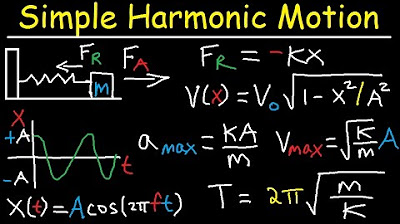
Simple Harmonic Motion, Mass Spring System - Amplitude, Frequency, Velocity - Physics Problems

01 - Oscillations And Simple Harmonic Motion, Part 1 (Physics Tutor)

AP Physics 1 review of Waves and Harmonic motion | Physics | Khan Academy

AP Physics Workbook 6.C Equations of Motion for Simple Harmonic Motion

Simple Harmonic Motion - Springs in series vs parallel, and vertical springs

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsTutorialHarmonicMotionSpringOscillatorsHookesLawFrequencyCalculationAngularFrequencyMechanicalWavesEducationalContentScienceLearningMathematicalPhysics