AP Physics 1: Simple Harmonic Motion Review

Flipping Physics
27 May 201512:32
EducationalLearning
32 Likes 10 Comments

TLDRIn this engaging lesson, Mr. P delves into the concept of simple harmonic motion as it pertains to the AP Physics 1 exam. He explains the dynamics of a mass-spring system on a frictionless surface, highlighting the role of the restoring force and how it leads to the oscillation between equilibrium positions. The discussion progresses to cover the relationship between force, displacement, and acceleration, and how these elements contribute to the conservation of mechanical energy. The lesson also touches on the equations for the period of a mass-spring system and a pendulum, emphasizing the constancy of periods in the absence of external influences like gravity or mass changes. The session concludes with a reinforcement of the principles of mechanical energy conservation and the independence of period from amplitude in both systems.

Takeaways
  • πŸ“ˆ Simple harmonic motion (SHM) is a fundamental topic for the AP Physics 1 exam, exemplified by a mass-spring system on a frictionless surface.
  • πŸ‹οΈ The restoring force in SHM, which is the force exerted by the spring, is always directed towards the equilibrium position and increases proportionally with displacement.
  • πŸ“Œ The amplitude of SHM is the maximum displacement of the object from its equilibrium position, and it determines the energy of the system.
  • πŸš€ Newton's Second Law applies to SHM, where the net force (and thus acceleration) at the equilibrium position is zero, and at the amplitude positions is at its maximum.
  • πŸ”„ The motion in SHM is cyclical, with the object moving back and forth between extreme positions without friction, theoretically continuing forever.
  • πŸ“Š The position of the mass in SHM can be described by the equation x = A * cos(2Ο€ft), where A is the amplitude and f is the frequency.
  • πŸ“ˆ The graphs of position, velocity, and acceleration in SHM show distinct patterns: zero velocity at extreme positions, maximum velocity at the equilibrium position, and maximum acceleration at the amplitude positions.
  • 🌐 The period of a mass-spring system is independent of gravity and depends on the mass and spring constant, given by T = 2Ο€βˆš(m/k).
  • πŸŒ™ On the moon, the period of a mass-spring system remains the same, but the period of a pendulum increases due to the lower gravitational acceleration.
  • πŸ”„ The conservation of mechanical energy is a key concept in SHM, as the total mechanical energy (kinetic plus potential) remains constant throughout the motion.
  • πŸ”— For further study, resources such as review lessons and lecture notes are available on the Flipping Physics website.
Q & A

  • What is simple harmonic motion?

    -Simple harmonic motion is a type of periodic motion where an object moves back and forth along a straight line, experiencing a restoring force that is proportional to the displacement from its equilibrium position and directed towards that position.

  • What is a typical example of an object undergoing simple harmonic motion?

    -A horizontal mass-spring system on a frictionless surface is a typical example of an object undergoing simple harmonic motion.

  • What happens when the mass in a mass-spring system is pulled to the right and released?

    -When the mass is pulled to the right and released, it will slide to the left, passing through the equilibrium position, and continue to move until it reaches the maximum displacement from the equilibrium position.

  • What is the force exerted by the spring at the equilibrium position?

    -At the equilibrium position, the force exerted by the spring is zero because the displacement from the equilibrium position is zero.

  • What is the restoring force in simple harmonic motion?

    -The restoring force in simple harmonic motion is the force exerted by the spring, which is always directed towards the equilibrium position and increases proportionally with the displacement from that position.

  • What is the maximum displacement from the equilibrium position called?

    -The maximum displacement from the equilibrium position is called the amplitude.

  • How does the velocity of the mass change at the extreme positions and the equilibrium position in simple harmonic motion?

    -At the extreme positions (one and three), the velocity of the mass is zero because it changes direction, while at the equilibrium position (two), the mass has its maximum magnitude velocity.

  • What is the relationship between the angular frequency and the frequency in simple harmonic motion?

    -The angular frequency (omega) is equal to two pi times the frequency (f), which is derived from the angular velocity equation.

  • How is the position of an object in simple harmonic motion described?

    -The position of an object in simple harmonic motion is described by the equation: position equals amplitude times the cosine of (two pi times frequency times time).

  • What major physics concept does the total mechanical energy graph in simple harmonic motion illustrate?

    -The total mechanical energy graph in simple harmonic motion illustrates the Conservation of Mechanical Energy, as the sum of kinetic and potential energies remains constant throughout the motion without friction.

  • How do the periods of a mass-spring system and a pendulum change when taken to the moon?

    -The period of the mass-spring system remains unchanged because it does not depend on gravity. However, the period of the pendulum increases because it is inversely related to the square root of the acceleration due to gravity, which is less on the moon.

  • How do the periods of a mass-spring system and a pendulum change when their masses are increased?

    -The period of the pendulum remains the same because it is independent of mass. The period of the mass-spring system increases because it is directly proportional to the square root of the mass of the system.

Outlines
00:00
πŸ“š Introduction to Simple Harmonic Motion

This segment introduces the concept of simple harmonic motion (SHM) as it pertains to the AP Physics 1 exam. It uses a horizontal mass-spring system on a frictionless surface to illustrate SHM. The video explains the equilibrium position, the displacement of the mass from this position, and the spring's restoring force that drives SHM. It also discusses the relationship between the spring constant, displacement, and velocity, and how these factors contribute to the object's motion. The segment further compares SHM to circular motion, using trigonometric functions to describe the object's position and relating it to angular velocity and period.

05:01
πŸ“ˆ Graphs of Simple Harmonic Motion

This part of the script delves into the graphical representation of SHM. It discusses the position graph, highlighting the oscillation between positions one, two, and three, and the cosine function's role in describing this motion. The script emphasizes the importance of using radians in the equations. It also covers the velocity and acceleration graphs, explaining how velocity and acceleration change at extreme positions and at the equilibrium position. The segment concludes with a discussion on mechanical energy conservation in SHM, demonstrating that kinetic and potential energies interchange but the total mechanical energy remains constant.

10:01
🌐 Period of Oscillation and Energy Conservation

In this section, the focus is on the period of oscillation for both mass-spring systems and pendulums in the context of SHM. It provides formulas for calculating the period of each system and discusses how the period is affected by factors such as gravity and mass. The script clarifies that while the period of a mass-spring system is independent of its mass and amplitude, the period of a pendulum is affected by the length of the pendulum and the acceleration due to gravity. The segment wraps up by reinforcing the concept of mechanical energy conservation in SHM, emphasizing that no external forces or friction are present to alter the system's total mechanical energy.

Mindmap
Keywords
πŸ’‘Simple Harmonic Motion
Simple Harmonic Motion (SHM) is a type of periodic motion where an object moves back and forth along a straight line under the influence of a restoring force that is proportional to the displacement from its equilibrium position. In the video, the horizontal mass-spring system is used as an example of SHM, where the mass oscillates between positions of maximum displacement (amplitude) and the equilibrium position without friction, illustrating the concept of a restoring force that pulls the mass back towards the equilibrium point.
πŸ’‘Restoring Force
A restoring force is the force that brings an object back to its equilibrium position in simple harmonic motion. It is always directed towards the equilibrium position and increases proportionally with the displacement from that position. In the context of the video, the force exerted by the spring on the mass is the restoring force, ensuring that the mass oscillates back and forth without stopping.
πŸ’‘Amplitude
Amplitude refers to the maximum displacement of an object from its equilibrium position during simple harmonic motion. It is a measure of the extent of the oscillation and is a constant value for a system undergoing SHM without damping. In the video, the amplitude is the distance the mass moves away from the equilibrium position at points one and three.
πŸ’‘Equilibrium Position
The equilibrium position is the point at which the net force acting on an object is zero, and it is the position where the object would remain if no external forces were applied. In the context of the video, the equilibrium position is where the mass would stay if not disturbed, with the spring force balancing any external forces and the mass not moving.
πŸ’‘Displacement
Displacement in the context of simple harmonic motion is the distance an object is from its equilibrium position. It is a vector quantity that points in the direction of the object's current position relative to the equilibrium point. In the video, displacement is used to describe how far the mass is from the equilibrium position along the horizontal axis.
πŸ’‘Acceleration
Acceleration is the rate of change of velocity of an object with respect to time. In simple harmonic motion, the acceleration is directly proportional to the displacement from the equilibrium position and is directed towards that position. The magnitude of the acceleration is greatest at the points of maximum displacement and is zero at the equilibrium position. In the video, the mass's acceleration is zero at position two (equilibrium) and maximum at positions one and three (maximum displacement).
πŸ’‘Velocity
Velocity is the speed of an object in a given direction. In simple harmonic motion, the velocity of an object changes as it moves through its cycle. The object has zero velocity at the points of maximum displacement (amplitude) and maximum velocity at the equilibrium position. The velocity is also indicated by the direction of motion; positive or negative, depending on whether the mass is moving to the right or left.
πŸ’‘Mechanical Energy
Mechanical energy is the sum of kinetic energy and potential energy in a mechanical system. In the context of simple harmonic motion without friction or external work, the mechanical energy remains constant, illustrating the principle of conservation of mechanical energy. The kinetic energy is highest when the mass is at the equilibrium position, and the potential energy is highest at the amplitude points.
πŸ’‘Period
The period of a motion is the time taken for one complete cycle of the motion. For simple harmonic motion, the period can be calculated using specific formulas depending on the system. The period of a mass-spring system is independent of the amplitude and is related to the mass and the spring constant, while the period of a pendulum is related to its length and the acceleration due to gravity.
πŸ’‘Conservation of Mechanical Energy
The principle of conservation of mechanical energy states that in a closed system with no external forces or friction, the total mechanical energy (sum of kinetic and potential energy) remains constant. This concept is illustrated in the video by showing that the total mechanical energy of the mass-spring system does not change throughout its oscillation, demonstrating the conservation of mechanical energy in simple harmonic motion.
πŸ’‘Angular Frequency
Angular frequency, denoted by Ο‰ (omega), is the rate of change of the angle in radians per unit time and is directly related to the frequency of oscillation. It is used in the equations describing simple harmonic motion to relate the position of the oscillating object to time. In the video, angular frequency is derived from the angular velocity and is used to express the position of the mass in the mass-spring system as a function of time.
Highlights

Review of simple harmonic motion topics for AP Physics 1 exam.

A horizontal mass-spring system on a frictionless surface exemplifies simple harmonic motion.

The force of the spring is proportional to the displacement from the equilibrium position and is always directed towards it.

At the equilibrium position, the displacement is zero, the spring force is zero, and the velocity of the mass is at its maximum.

The maximum displacement from the equilibrium position is called the amplitude.

Simple harmonic motion continues indefinitely without friction, exhibiting a continuous back-and-forth movement.

The velocity of the block is zero at the points of maximum displacement (positions one and three) and maximum at the equilibrium position (position two).

The restoring force of the spring is responsible for causing simple harmonic motion.

The position of the mass-spring system is described by the equation position equals amplitude times the cosine of two pi times frequency times time.

The graph of position follows a cosine wave pattern, oscillating between maximum and minimum displacements.

The velocity graph shows zero velocity at maximum displacements and maximum velocity at the equilibrium position.

The acceleration graph reflects maximum magnitude acceleration at the maximum displacements and zero acceleration at the equilibrium position.

Simple harmonic motion is not uniformly accelerated motion, thus requiring different equations for analysis.

Mechanical energy is conserved in simple harmonic motion due to the absence of friction and external work.

The period of a mass-spring system is independent of its amplitude and is determined by the mass and spring constant.

The period of a pendulum is related to its length and the acceleration due to gravity, and is also independent of its amplitude.

On the moon, the period of a pendulum increases due to the lower gravity, while the period of a mass-spring system remains unchanged.

Increasing the mass of a mass-spring system increases its period, while the period of a pendulum remains unchanged as it is independent of mass.

The review concludes with an introduction to the next topic, waves, and a reference to additional resources on the instructor's website.

Transcripts

Browse More Related Video

Simple Harmonic Motion - Complete Review of the Mass-Spring System

2021 Live Review 6 | AP Physics 1 | Understanding Simple Harmonic Motion

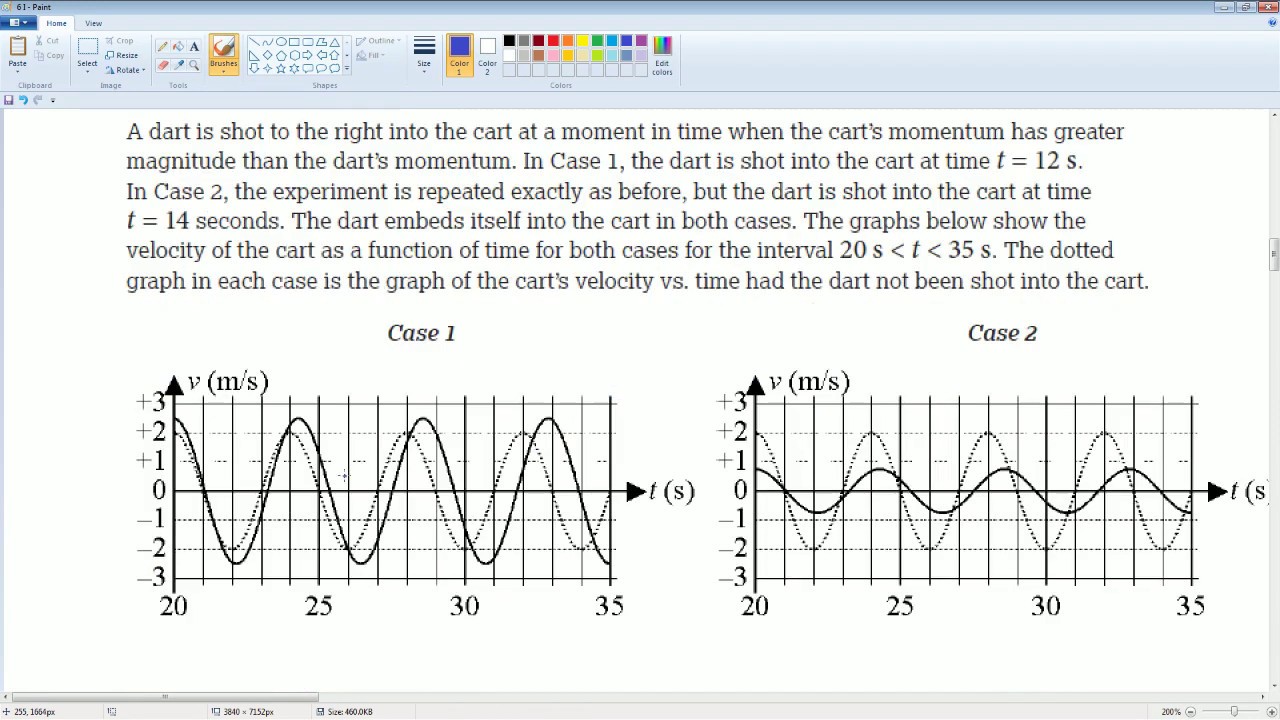
AP Physics Workbook 6.I Changing Mass and Period of a Mass Spring SYstem

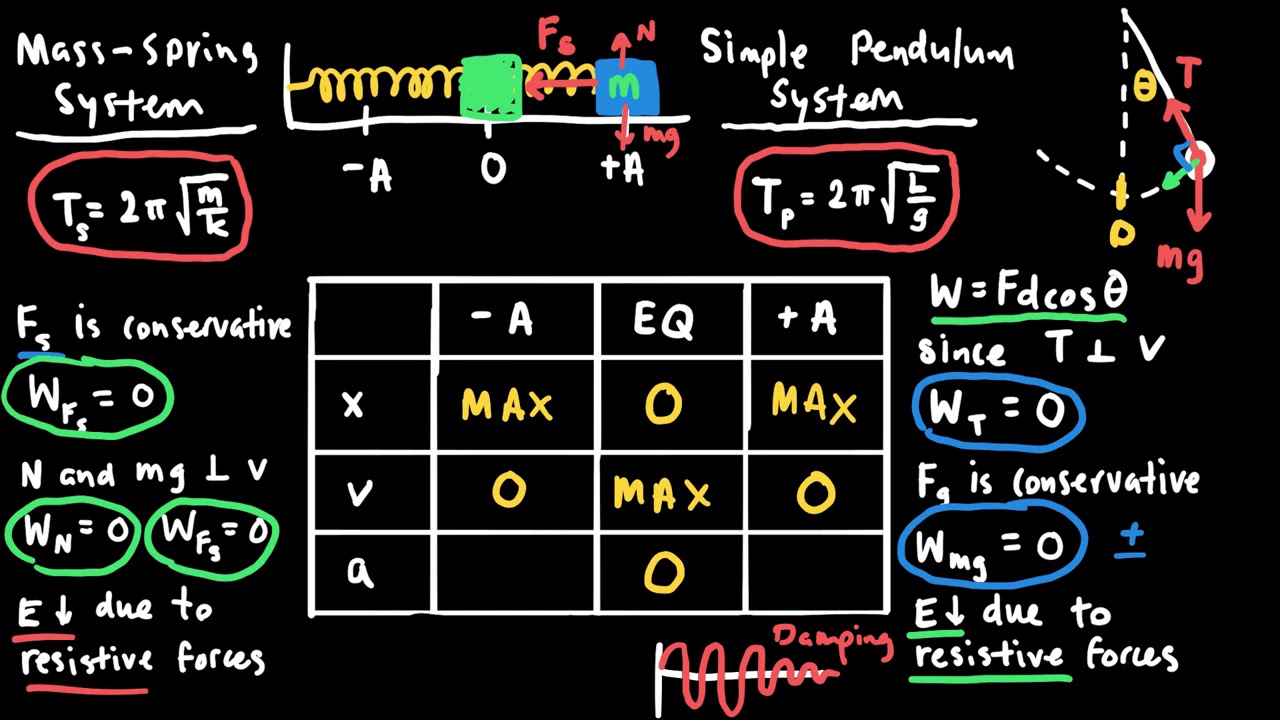
AP Physics 1 Simple Harmonic Motion, Mechanical Waves, and Sound Review

AP Physics Workbook 6.K Mass and Period of Mass Spring System

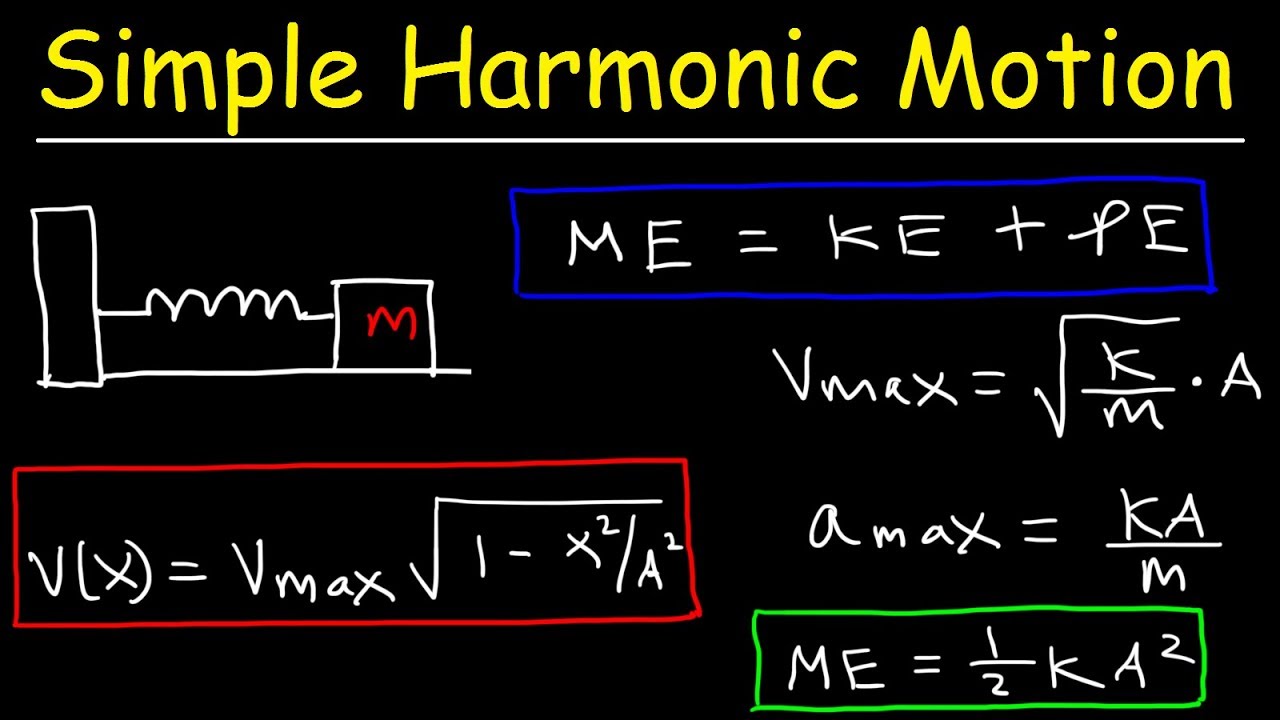
Energy In a Simple Harmonic Oscillator - Maximum Velocity & Acceleration Calculations

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsEducationHarmonicMotionAPPhysics1MechanicalEnergyConservationLawMassSpringSystemPendulumMotionOscillationAnalysisFlippingPhysicsMrP