Simple Harmonic Motion - Complete Review of the Mass-Spring System
TLDRThis tutorial delves into the principles of simple harmonic motion, focusing on the horizontal spring-mass system. It explains how to derive equations for position, velocity, and acceleration, and discusses period, frequency, and angular frequency. The video also explores energy conservation, highlighting the transformation between potential energy in the spring and kinetic energy of the mass. Practical examples and problem-solving techniques are provided to illustrate the concepts, emphasizing the independence of the oscillation period from amplitude and the role of Hooke's Law in determining spring force.
Takeaways
- 📚 The tutorial covers the fundamental concepts of simple harmonic motion, focusing on the horizontal spring and mass system.
- 🔍 It explains how to analyze forces involved and derive equations for position, velocity, and acceleration of the mass in motion.
- 📈 The video demonstrates the calculation of period, frequency, and angular frequency for a simple harmonic oscillator.
- 🌟 It introduces Hooke's Law, which quantifies the spring force as a negative constant times the displacement (F = -kx).
- 🔄 The tutorial explores the energy dynamics in a spring-mass system, including potential energy stored in the spring and kinetic energy of the mass.
- ⚖️ It uses Newton's second law to establish the relationship between acceleration, force, and mass in the context of simple harmonic motion.
- 📉 The script discusses how to solve for the position of the mass over time using calculus and the characteristics of the spring and mass system.
- 🔢 The amplitude, angular frequency, and phase constant are identified as key parameters in describing the motion of a simple harmonic oscillator.
- 🔧 The video addresses how changes in mass and spring constant affect the period of oscillation, while amplitude does not.
- 📚 It provides example problems to illustrate the application of equations for position, velocity, and acceleration in different scenarios.
- 💡 The final part of the script delves into energy conservation, potential energy, and work done by the spring force during motion.
Q & A
What is the main topic of the tutorial?
-The main topic of the tutorial is simple harmonic motion, focusing on the horizontal spring and mass system.
What are the key properties of a spring that can be determined from Hooke's Law?
-Hooke's Law states that the spring force is given by the negative spring constant (K) multiplied by the displacement (X). The key properties determined from this law are the spring constant, which indicates the stiffness of the spring, and the displacement from the equilibrium position.
What is the period of oscillation and how is it measured?
-The period of oscillation is the time it takes for the mass to complete one full cycle of back-and-forth motion. It is measured in seconds.
How can the period of oscillation be calculated?
-The period of oscillation can be calculated using the formula T = 2π * sqrt(m/k), where 'm' is the mass and 'k' is the spring constant.
What factors affect the period of oscillation of a simple harmonic oscillator?
-The period of oscillation is affected by the mass (m) and the spring constant (k). A larger mass or a smaller spring constant results in a longer period.
What is the relationship between angular frequency (ω) and the linear frequency (f)?
-The angular frequency (ω) is related to the linear frequency (f) by the equation ω = 2πf. The linear frequency is measured in hertz and represents the number of oscillations per second.
What is the significance of the phase constant in the context of simple harmonic motion?
-The phase constant in simple harmonic motion is related to the initial conditions of the system. It affects the starting point of the oscillation on the position-time graph and can influence the initial velocity of the mass.
How does the amplitude of oscillation affect the maximum velocity of the mass?
-The maximum velocity of the mass is directly proportional to the amplitude of oscillation. A larger amplitude results in a greater maximum velocity, assuming the spring constant and mass remain constant.
What is the difference between potential energy stored in the spring and kinetic energy of the mass?
-Potential energy stored in the spring is the energy associated with the spring's deformation and is given by (1/2)kx^2. Kinetic energy is the energy of motion and is given by (1/2)mv^2. The spring's potential energy is converted to the mass's kinetic energy as the mass moves away from the equilibrium position.
How is the work done by the spring force related to the potential energy stored in the spring?
-The work done by the spring force as it stretches or compresses is equal to the change in potential energy stored in the spring. This relationship is expressed as the work done by the spring force being equal to the difference in potential energy between the initial and final positions.
Why is the period of oscillation independent of the amplitude for a simple harmonic oscillator?
-The period of oscillation is independent of the amplitude because it is determined solely by the mass and spring constant according to the formula T = 2π * sqrt(m/k). The amplitude does not affect these two factors, thus it does not influence the period.
How can the velocity of a mass in simple harmonic motion be determined at any given time?
-The velocity of a mass in simple harmonic motion at any given time can be determined by differentiating the position function with respect to time, which yields the velocity function. The velocity is given by -ωA * sin(ωt + φ), where ω is the angular frequency, A is the amplitude, t is time, and φ is the phase constant.
What is the condition for the total mechanical energy of a simple harmonic oscillator to be conserved?
-The total mechanical energy of a simple harmonic oscillator is conserved when there is no energy dissipation, such as in the absence of friction or other non-conservative forces.
How can the work done by the spring force be calculated when stretching the spring?
-The work done by the spring force when stretching it is calculated by integrating the force with respect to the displacement from the initial to the final position, which is given by the integral of Hooke's Law (-kx) with respect to x from x_initial to x_final.
Outlines
🌀 Introduction to Simple Harmonic Motion Tutorial
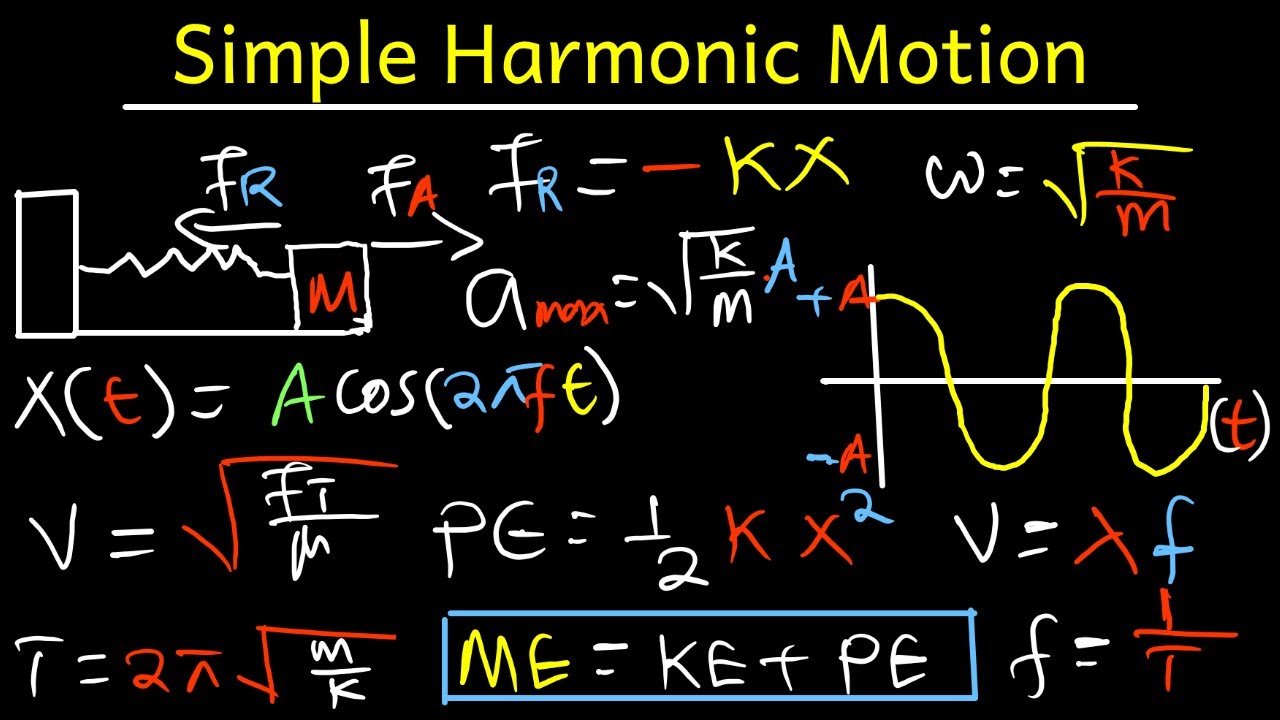
The video begins with an introduction to simple harmonic motion, focusing on a horizontal spring-mass system. The narrator, Physics Ninja, plans to analyze the forces involved when the spring is stretched and released, leading to periodic motion. The tutorial will cover the derivation of equations for position, velocity, and acceleration, and explain how to calculate the period, frequency, and angular frequency of oscillation. Additionally, the video will address energy concepts, such as potential energy stored in the spring and kinetic energy of the mass, with example problems to illustrate the concepts.
🔍 Analyzing Forces in a Spring-Mass System
This paragraph delves into the forces acting on the mass in a spring-mass system. The narrator discusses the setup of the system with a mass attached to a spring and the importance of the equilibrium position. It introduces Hooke's Law, which quantifies the spring force as a product of the spring constant (K) and the displacement from the equilibrium (X), with the force being a restoring force directed opposite to the displacement. The paragraph also explains how to calculate the spring force in both stretching and compressing scenarios.
📚 Newton's Second Law and Dynamics of SHM
The narrator applies Newton's second law to the spring-mass system to derive the equation of motion. By equating the net force (spring force) to mass times acceleration, the dynamics of the system are explored. The resulting differential equation is then solved using calculus, leading to the general solution for the position of the mass as a function of time, which is a cosine function with amplitude (A) and angular frequency (Ω). Initial conditions, such as the amplitude and release from rest, are also discussed.
⚙️ Calculating Angular Frequency and Period
The paragraph explains how to calculate the angular frequency and period of oscillation for a spring-mass system. The angular frequency (Ω) is derived as the square root of the spring constant (K) divided by the mass (m). The period (T) is then found by taking the reciprocal of the linear frequency, which is 2π times the frequency. The narrator also discusses how changes in mass and spring constant affect the period of oscillation.
🔄 The Independence of Period from Amplitude
This section emphasizes that the period of oscillation in simple harmonic motion is independent of the amplitude. The narrator explains that regardless of the amplitude, the period remains constant, which is a key characteristic of simple harmonic oscillators. The paragraph also discusses the phase angle and its relation to initial conditions, particularly when the system is released from rest.
📈 Sketching Solutions for SHM
The narrator provides a visual representation of the solutions for simple harmonic motion by sketching the position, velocity, and acceleration over time. The position graph is a cosine function, the velocity graph is a sine function with a negative sign, and the acceleration graph is a cosine function flipped upside down. These graphs help to visualize the behavior of the mass over one cycle of oscillation.
📘 Solving Example Problems in SHM
The paragraph presents an example problem involving a spring-mass system with given parameters. The narrator guides the viewer through finding the amplitude, angular frequency, phase constant, frequency, and period of the motion. Additionally, the spring constant is calculated using the known angular frequency and mass. The position, velocity, and acceleration functions of time are derived, and their initial values are evaluated at time equals zero.
👷♂️ Work Done by the Spring Force
This section discusses the work done by the spring force when stretching a spring. The narrator contrasts the work done by gravity, which can be calculated using a simple formula for constant forces, with the work done by the spring force, which requires integration due to its variable nature. The work done by the spring is found by integrating the spring force over the displacement, leading to an expression involving the square of the displacement.
⚡️ Energy Conservation in SHM
The narrator explores energy conservation in the context of simple harmonic motion. The potential energy stored in the spring is defined and related to the work done by the spring force. The total mechanical energy of the system is conserved in the absence of non-conservative forces like friction. The relationship between the total energy, kinetic energy, and spring potential energy is discussed, and an expression for the speed of the mass as a function of position is derived.
📊 Graphing Energy in SHM
The paragraph covers the two types of graphs typically used to represent energy in simple harmonic motion: energy versus position and energy versus time. The narrator explains how to plot the spring potential energy, kinetic energy, and total energy on these graphs, emphasizing the conservation of total energy and the periodic nature of the motion.
🧩 SHM Energy Problems and Calculations
The final paragraph presents a problem involving a mass with a given amplitude and period, and the narrator demonstrates how to use the energy concepts to find the total energy, maximum speed, and the position where the speed is half of its maximum value. The calculations involve using the period to find the spring constant and then applying energy conservation principles to solve for the desired quantities.
Mindmap
Keywords
💡Simple Harmonic Motion
💡Spring Constant
💡Hooke's Law
💡Period of Oscillation
💡Angular Frequency
💡Kinematic Quantities
💡Potential Energy
💡Kinetic Energy
💡Energy Conservation
💡Differential Equation
Highlights
Introduction to simple harmonic motion tutorial covering horizontal spring and mass system analysis.
Explanation of how to derive equations for position, velocity, and acceleration in simple harmonic motion.
Understanding the period, frequency, and angular frequency of a simple harmonic oscillator.
Analysis of forces in a spring system using Hooke's Law and its significance in calculating spring force.
The role of spring constant (K) in determining the stiffness of a spring and its unit of measurement.
Calculating the net force and acceleration of a mass in a spring system using Newton's Second Law.
Deriving the equation for the position of a mass as a function of time in simple harmonic motion.
The importance of initial conditions in determining the amplitude and phase of oscillation.
Relating angular frequency to the spring constant and mass to calculate the period of oscillation.
Demonstration of how the period of oscillation is independent of amplitude in simple harmonic motion.
Solving for the phase constant in the context of initial conditions for a spring-mass system.
Graphical representation of position, velocity, and acceleration over time in simple harmonic motion.
Energy analysis in a spring-mass system, including potential and kinetic energy conversion.
Calculating work done by spring force through integration of force over displacement.
Introduction of spring potential energy and its relation to the work done by the spring force.
Conservation of mechanical energy in a simple harmonic oscillator without external forces.
Derivation of velocity expression from energy conservation in simple harmonic motion.
Explaining the independence of total energy on the position of the mass in simple harmonic motion.
Problem-solving approach using energy conservation to find total energy, maximum speed, and specific positions in a spring-mass system.
Transcripts
Browse More Related Video
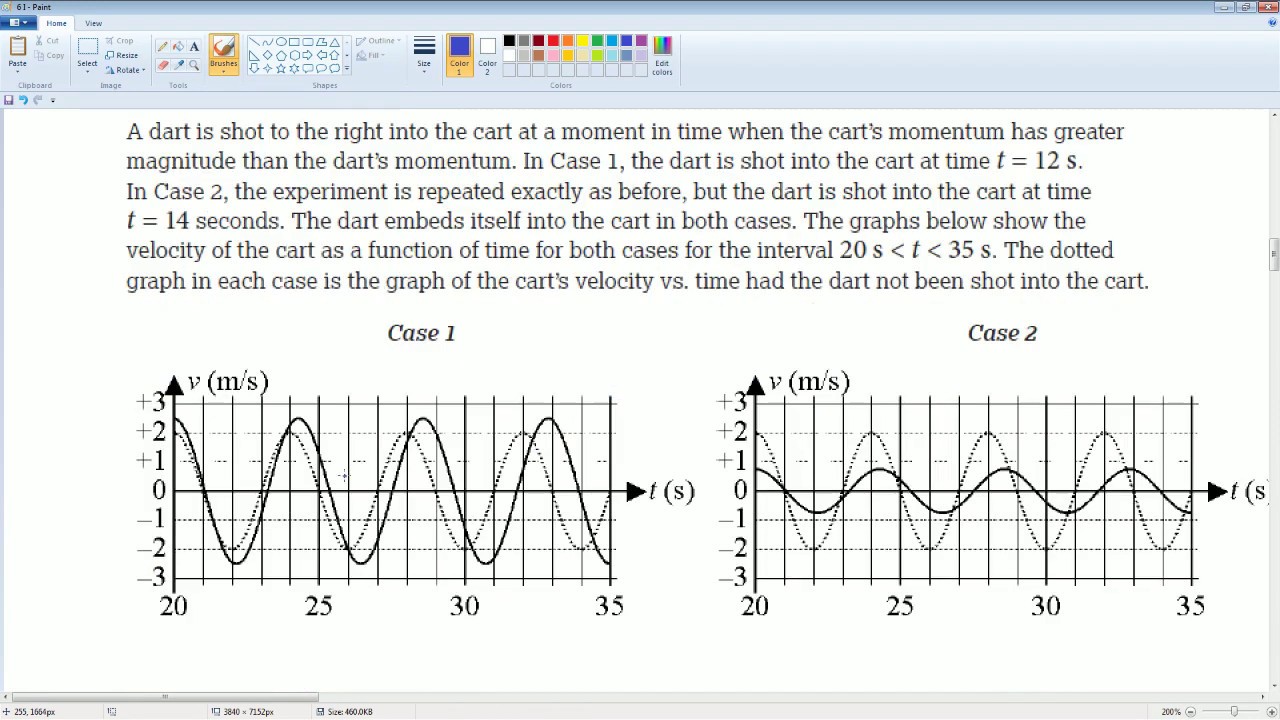
AP Physics Workbook 6.I Changing Mass and Period of a Mass Spring SYstem
How To Solve Simple Harmonic Motion Problems In Physics
Simple Harmonic Motion - Springs in series vs parallel, and vertical springs
AP Physics 1: Simple Harmonic Motion Review
Simple Harmonic Motion, Mass Spring System - Physics Full Topic
Simple Harmonic Motion, Mass Spring System - Amplitude, Frequency, Velocity - Physics Problems
5.0 / 5 (0 votes)
Thanks for rating: