AP Physics B - 2013 #2 (Springs)
TLDRThis script from a 2013 AP Physics B exam walkthrough addresses an energy-driven problem involving simple harmonic motion. It explains the work done by a spring on a 20 kg box moving on a frictionless surface, calculating the spring's work, spring constant, maximum acceleration, and frequency of oscillation. The explanation includes diagrams and a step-by-step process to solve for each variable, emphasizing the importance of understanding energy transfer and Hooke's law in physics.
Takeaways
- 📦 The problem involves a 20 kg box on a frictionless surface moving at 4 m/s which hits and compresses a spring attached to a wall.
- 🔄 The box's kinetic energy is converted to elastic potential energy when it compresses the spring.
- ✋ The work done by the spring on the box is negative because it reduces the box's kinetic energy.
- ⚙️ The magnitude of the work done by the spring is 160 joules, calculated using the initial kinetic energy of the box.
- 🔧 The spring constant (k) is determined to be 1280 N/m using the formula for elastic potential energy and the work done by the spring.
- ⚡ The maximum acceleration of the box occurs when the spring is fully compressed, calculated to be 32 m/s² using Hooke's law and Newton's second law.
- ⏲️ The frequency of the box's oscillation is 1.27 Hz, derived from the formula for the frequency of simple harmonic motion.
- 📉 The kinetic energy of the box as a function of position is a curve that peaks at zero compression and drops to zero at maximum compression and expansion.
- 📈 The acceleration of the box as a function of position is a linear relationship, reaching maximum negative acceleration at full compression and maximum positive acceleration at full expansion.
- 📊 Directional information is crucial for understanding the acceleration graph, but not as important for the kinetic energy graph.
Q & A
What is the mass of the box in the given problem?
-The mass of the box is 20 kilograms.
What is the initial speed of the box before it hits the spring?
-The initial speed of the box is 4 meters per second.
Is the surface on which the box is moving frictionless?
-Yes, the surface is frictionless.
What is the significance of the box hitting and compressing the spring?
-The box compressing the spring transforms its kinetic energy into potential energy, causing it to oscillate back and forth.
Why is the work done by the spring considered negative?
-The work done by the spring is considered negative because it acts against the direction of the box's motion, reducing its kinetic energy.
How is the magnitude of the work done by the spring calculated?
-The magnitude of the work done by the spring is equal to the initial kinetic energy of the box, calculated as \( \frac{1}{2} m v^2 \).
What is the formula for the spring constant (k) and how is it calculated in this problem?
-The formula for the spring constant (k) is \( k = \frac{2W}{x^2} \), where W is the work done and x is the compression distance. In this problem, it is calculated as \( k = \frac{2 \times 160 \, \text{J}}{(0.5 \, \text{m})^2} = 1280 \, \text{N/m} \).
When does the maximum acceleration of the box occur and how is it calculated?
-The maximum acceleration occurs when the spring is fully compressed. It is calculated using Newton's second law, \( a = \frac{kx}{m} \).
What is the frequency of the box's oscillation and how is it calculated?
-The frequency of the box's oscillation is calculated using the formula \( f = \frac{1}{2\pi} \sqrt{\frac{k}{m}} \). In this problem, it is found to be 1.27 Hz.
How is the kinetic energy of the box as a function of position sketched?
-The kinetic energy is maximum at x = 0 (initial point), zero at maximum compression and expansion (x = ±0.5), and follows an exponential curve.
How is the acceleration of the box as a function of position sketched?
-The acceleration is zero at x = 0, maximum negative at maximum compression (x = 0.5), and maximum positive at maximum expansion (x = -0.5), following a linear relationship.
Outlines
📦 Energy and Work in Spring Systems
The problem involves a 20 kg box on a frictionless surface moving at 4 m/s that compresses a spring by 0.5 meters. The focus is on the work done by the spring as it compresses and the energy transformations involved. Initially, the box has kinetic energy, which converts to elastic potential energy as the spring compresses. The work done by the spring is negative since it reduces the box's kinetic energy. The magnitude of this work equals the initial kinetic energy of the box, calculated to be 160 joules.
🪫 Calculating Spring Constant and Maximum Acceleration
To find the spring constant (k), the potential energy stored in the spring is equated to the work done, yielding k = 1280 N/m. The maximum acceleration occurs when the spring is fully compressed, calculated using Newton's second law, giving an acceleration of 32 m/s². This acceleration is directionally dependent, but since only magnitude is requested, the direction is disregarded.
🌀 Simple Harmonic Motion and Frequency Calculation
The frequency of the box's oscillation is determined using the formula for simple harmonic motion, resulting in a frequency of 1.27 Hz. The kinetic energy of the box varies exponentially with position, reaching zero at maximum compression and expansion of the spring. The acceleration also varies linearly with position, with maximum values at maximum compression and expansion.
📊 Graphing Kinetic Energy and Acceleration
Graphs are sketched for kinetic energy and acceleration as functions of position. The kinetic energy graph is exponential, with maximum values at zero compression and zero at maximum compression and expansion. The acceleration graph is linear, showing maximum negative acceleration at maximum compression and maximum positive acceleration at maximum expansion.
Mindmap
Keywords
💡Energy
💡Simple Harmonic Motion
💡Kinetic Energy
💡Potential Energy
💡Spring Constant
💡Work
💡Acceleration
💡Frequency
💡Newton's Second Law
💡Hooke's Law
Highlights
The problem involves energy and simple harmonic motion concepts.
A 20 kg box moves on a frictionless surface at 4 m/s and hits a spring.
The spring compresses 0.5 meters and the box oscillates back and forth.
The spring does negative work on the box when it first hits.
The work done by the spring is equal to the initial kinetic energy of the box.
The magnitude of the work done is calculated to be 160 Joules.
The spring constant is determined using the formula k = 2W/x^2.
The spring constant is found to be 1280 N/m.
The maximum acceleration of the box occurs when the spring is fully compressed.
The maximum acceleration is calculated to be 32 m/s^2.
The frequency of the box's oscillation is determined using the formula f = 1/(2π√(k/m)).
The frequency of oscillation is found to be 1.27 Hz.
A graph of kinetic energy vs. position shows an exponential relationship.
A graph of acceleration vs. position shows a linear relationship.
The problem is broken down into multiple parts, each worth a few points.
The solution process emphasizes understanding the physics concepts and applying them correctly.
Transcripts
Browse More Related Video
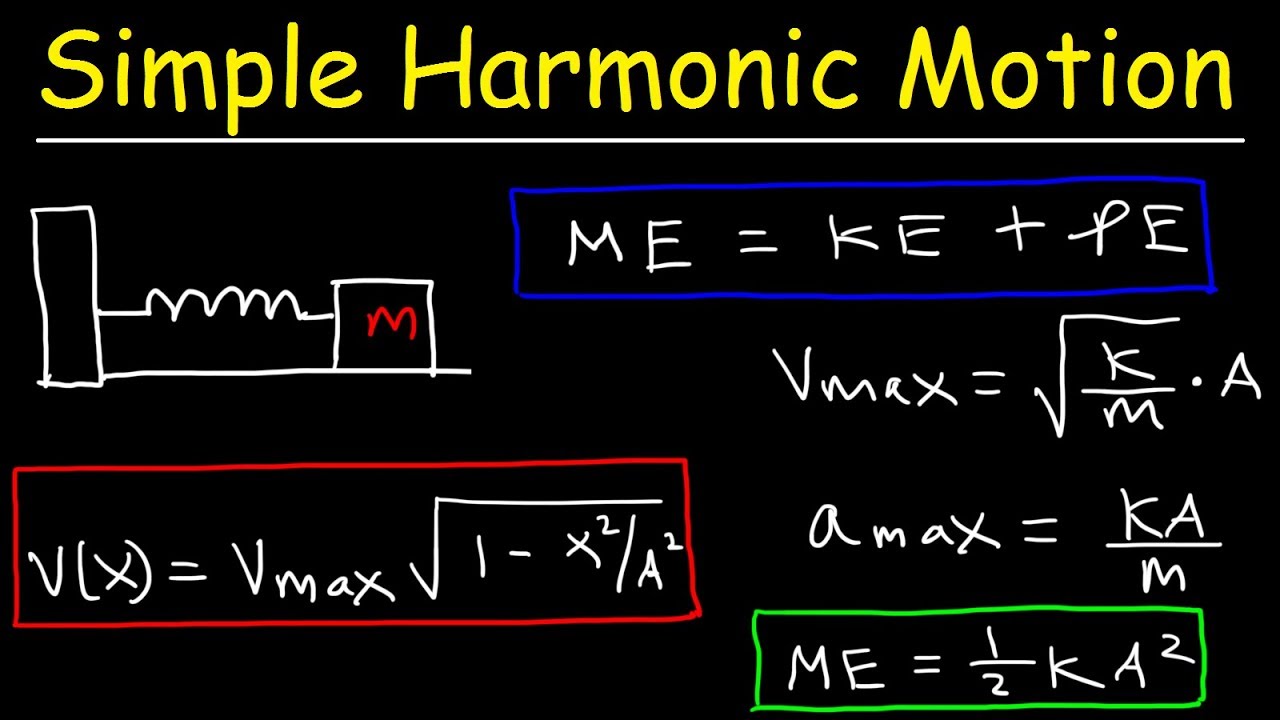
Energy In a Simple Harmonic Oscillator - Maximum Velocity & Acceleration Calculations
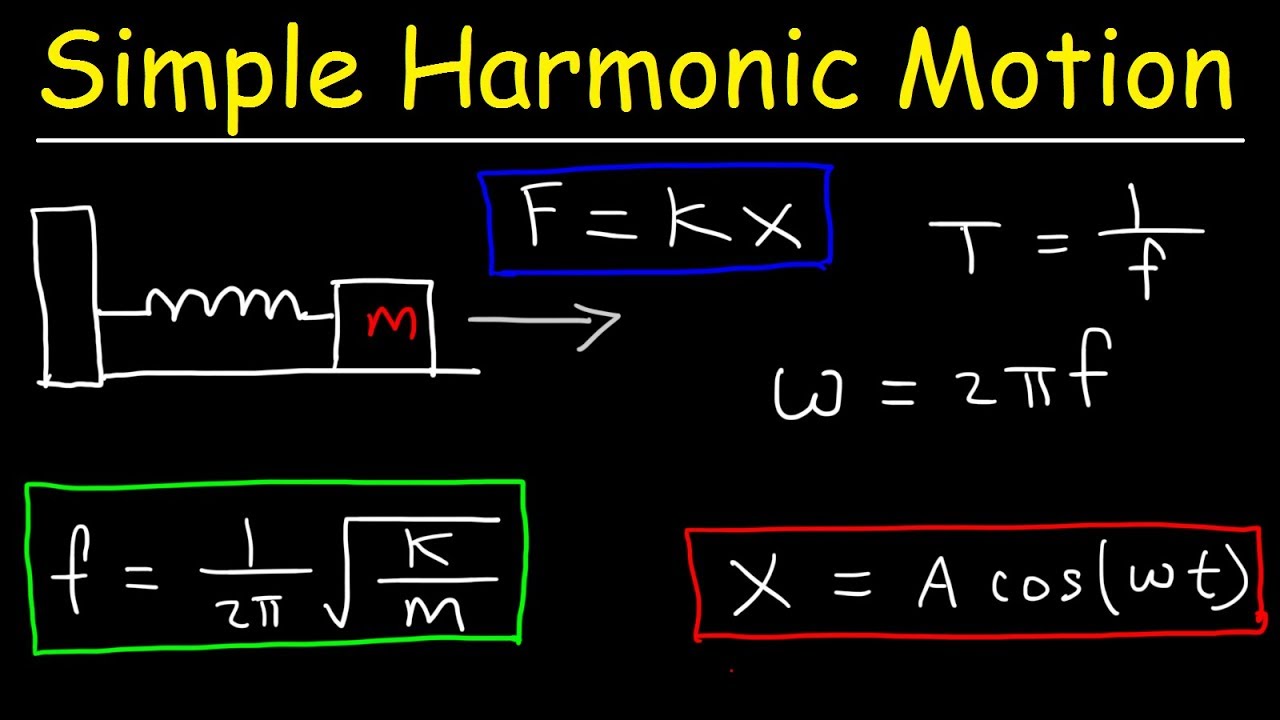
How To Solve Simple Harmonic Motion Problems In Physics
AP Physics Workbook 6.I Changing Mass and Period of a Mass Spring SYstem

AP Physics B - 2013 #5 (Thermodynamics - Work)

Simple Harmonic Motion - Complete Review of the Mass-Spring System

Work Problems | Calculus 2 Lesson 8 - JK Math
5.0 / 5 (0 votes)
Thanks for rating: