Preface | MIT Calculus Revisited: Single Variable Calculus
TLDRIn this introductory Calculus Revisited lecture by Professor Herb Gross, the fundamental concepts of calculus are explored, including limits, derivatives, and integrals. The course structure is outlined, emphasizing the importance of textbooks, supplementary notes, and study guides. The professor illustrates the practical applications of calculus, such as calculating instantaneous speed and areas under curves, and highlights the historical development of calculus, including the method of exhaustion and the paradoxes posed by Zeno. The lecture sets the stage for a deeper dive into the mathematical tools essential for engineers and physicists.
Takeaways
- 📚 The lecture introduces 'Calculus Revisited', a course aimed at providing an in-depth understanding of calculus with a focus on its applications and theoretical foundations.
- 🎓 Professor Herb Gross emphasizes the importance of the textbook, lectures, supplementary notes, and the study guide as integral components of the course material.
- 📈 The course structure includes pretests, learning exercises, and a final examination to assess understanding and application of concepts.
- 🔍 Calculus is defined as an extension of high school mathematics with the addition of the limit concept, which is central to both differential and integral calculus.
- 🏎️ The concept of instantaneous speed is introduced as an example of a rate of change that calculus helps to understand, contrasting it with the average speed.
- 🤔 The indeterminate form 0/0 is highlighted as a key issue in calculus, illustrating the need for a rigorous definition that avoids such undefined expressions.
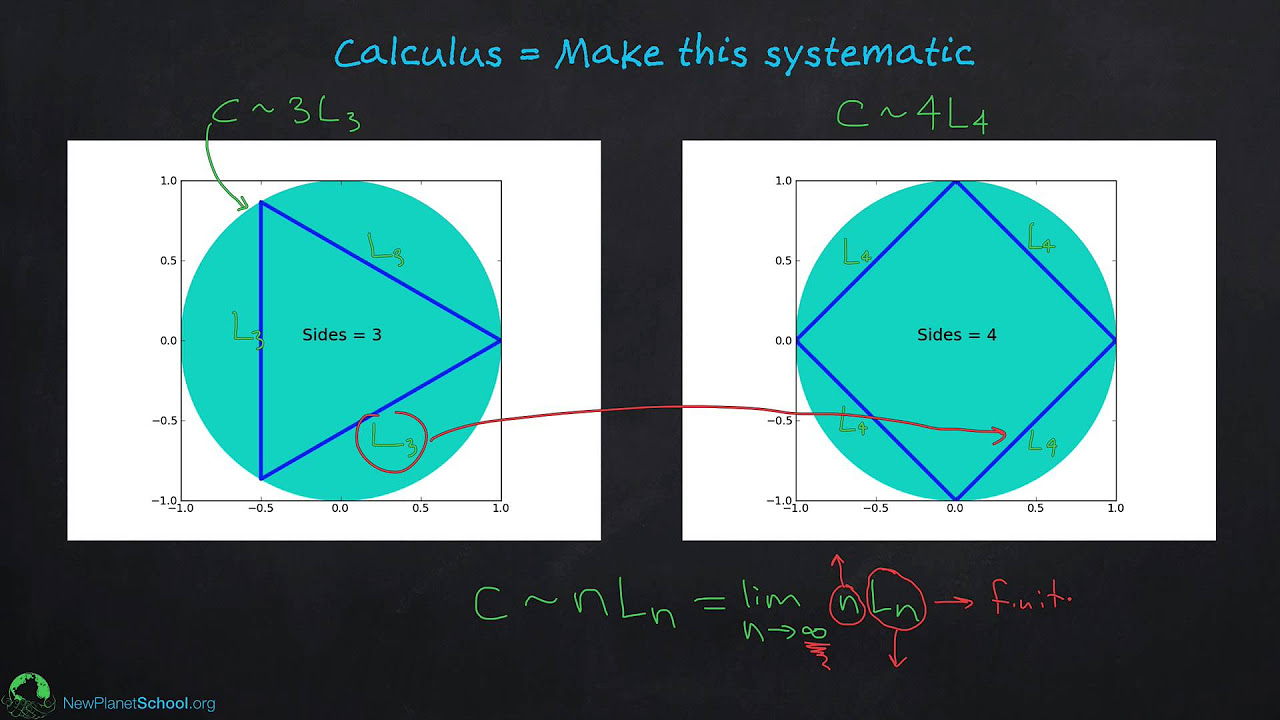
- 📉 The method of exhaustion, used by the Ancient Greeks, is presented as an early approach to calculating areas under curves, which is foundational to integral calculus.
- 📈 The physical interpretation of the area under a curve is explained, showing how it can represent quantities such as distance traveled in physics problems.
- 🔗 The fundamental theorem of integral calculus is mentioned as the key relationship that connects differential and integral calculus, showing their interdependence.
- 📊 The importance of limits in understanding both the tangent of a curve and the sum of areas under curves is underscored, highlighting their role in calculus.
- 📚 The course will delve into functions, limits, derivatives, integrals, and infinite series, building from foundational concepts to more complex applications.
Q & A
What is the main purpose of the 'Preface' lecture in the Calculus Revisited course?
-The 'Preface' lecture aims to provide an overview of both the course structure and content, including the hardware and software components, to prepare students for the material to be covered in the course.
What role does the textbook play in the Calculus Revisited course?
-The textbook serves as a core component of the course, offering deeper insights into the material than lectures alone can provide, and filling in any gaps that may exist in the lecture material.
What are the supplementary notes in the Calculus Revisited course intended to do?
-The supplementary notes are designed to provide additional knowledge where the textbook may leave gaps, ensuring a comprehensive understanding of the course material.
Can you explain the function of the study guide in the Calculus Revisited course?
-The study guide is the backbone of the course package, offering a breakdown of the course content, pretests, final examinations, and learning exercises that aim to engage students in applying the material and highlight the importance of the theoretical concepts.
How does Professor Herb Gross define calculus in the context of high school mathematics?
-Professor Gross defines calculus as high school mathematics with the addition of the limit concept, which is fundamental to both differential and integral calculus.
What is the fundamental concept that Professor Gross introduces to explain the idea of instantaneous speed?
-The fundamental concept introduced is the idea of having infinitely many pairs of observers getting closer and closer together without ever touching, which is used to approximate the instantaneous speed as the average speed between the observers.
Why is the expression 0/0 considered indeterminate in calculus?
-The expression 0/0 is considered indeterminate because any number multiplied by zero gives zero, thus making it impossible to determine a unique value for the expression.
What is the method of exhaustion as described in the script?
-The method of exhaustion is an ancient technique used to find the area under a curve by inscribing rectangles and summing their areas, then refining the approximation by increasing the number of divisions until the upper and lower bounds converge to the same value.
How does the concept of area under a curve relate to the physical world, according to the script?
-In the physical world, the area under a curve can represent quantities such as the distance traveled by a particle when its velocity is plotted against time.
What is the fundamental theorem of integral calculus and how does it relate to the concept of limits?
-The fundamental theorem of integral calculus relates the concept of areas (integral calculus) to rates of change (differential calculus). It shows that the area under a curve can be found by understanding how fast the height of the curve is changing, and vice versa, through the use of limits.
What are Zeno's paradoxes and how do they relate to the concept of infinite series in calculus?
-Zeno's paradoxes are a set of philosophical problems that question the possibility of motion and infinite divisibility of space and time. They relate to infinite series in calculus by illustrating the difficulty in understanding how an infinite number of actions can be completed in a finite amount of time, which is a concept that calculus addresses.
How does the script describe the importance of sets in the study of calculus?
-The script describes sets as the fundamental building block and the language of modern mathematics, essential for understanding functions, which are the foundation of calculus.
Outlines
📚 Introduction to Calculus Revisited Course
The video script begins with an introduction to MIT OpenCourseWare and a call for donations to support free educational resources. Professor Herb Gross greets viewers and introduces the first lecture of 'Calculus Revisited.' He outlines the structure of the course, including lectures, textbook, supplementary notes, and a study guide. The study guide is highlighted for its role in offering pretests, learning exercises, and examinations. The professor emphasizes the importance of the limit concept in calculus, distinguishing between average and instantaneous speed, and uses the example of observers measuring speed to illustrate the approach to calculating instantaneous speed.
🔍 The Concept of Instantaneous Speed and Limits
This paragraph delves deeper into the concept of instantaneous speed, contrasting it with average speed and discussing the problem of determining speed at a specific instant. The idea of bringing observers closer together to refine the measurement of speed is introduced, leading to the mathematical challenge of dividing by zero when the distance between observers is nil. The professor explains the indeterminate nature of 0/0 and the necessity of avoiding this expression, hinting at the use of functions and the limit concept to overcome this issue, which is foundational to calculus.
📉 Functions, Graphs, and the Definition of Differential Calculus
The script moves on to discuss functions and their graphical representation, using the example of a freely falling body to illustrate how functions can describe relationships over time. The concept of a graph as a visual representation of a function is introduced, with time as the input and distance as the output. The average speed is related to the slope of a line on the graph, and the idea of defining instantaneous speed through the limit of the change in distance over time as the time interval approaches zero is presented. This working definition is central to differential calculus, and the professor notes that while the definition remains constant, the complexity of calculating it can vary with different functions.
📏 The Method of Exhaustion and Integral Calculus
The fourth paragraph introduces the Ancient Greeks' method of exhaustion as a way to calculate the area under a curve, which is integral to integral calculus. The method involves dividing the area into rectangles and summing their areas to approximate the total area under the curve. The Greeks' technique is shown to be a precursor to the modern understanding of integral calculus, with the professor drawing a connection between the area under a curve and physical concepts such as distance traveled based on velocity over time.
🌐 The Relationship Between Differential and Integral Calculus
This section highlights the connection between the two branches of calculus: differential and integral. The professor discusses how the area under a curve can be related to the rate of change of the curve's height, and vice versa. The fundamental theorem of integral calculus, which links rates of change to areas, is alluded to as a key concept that will be explored in the course. The beauty of calculus is emphasized, particularly the unity between these two seemingly distinct branches.
∞ The Challenge of Infinite Sums and Zeno's Paradoxes
The script addresses the concept of infinite sums and their role in calculus, particularly in the context of Zeno's paradoxes. The Tortoise and the Hare problem is used to illustrate the difficulty of reconciling infinite processes with finite outcomes. The paradox is resolved by demonstrating that an infinite series can sum to a finite value, which is a central issue in understanding calculus and its applications.
📘 Course Overview and the Importance of Sets in Mathematics
The final paragraph provides an overview of the course content, which includes functions, limits, derivatives, integrals, and infinite series. The professor emphasizes the importance of understanding sets as the fundamental language of modern mathematics. The course will start with a digression on sets before delving into functions and progressing to more complex topics. The script concludes with a reminder of the course's goal to explore these concepts in depth and the professor bids farewell until the next session.
Mindmap
Keywords
💡Creative Commons license
💡Calculus
💡Lecture
💡Textbook
💡Supplementary notes
💡Study guide
💡Instantaneous speed
💡Limit concept
💡Integral calculus
💡Fundamental theorem of integral calculus
💡Infinite series
Highlights
Introduction to Calculus Revisited course and its structure, emphasizing the importance of lectures, textbook, supplementary notes, and the study guide.
The concept of calculus as an extension of high school mathematics with the introduction of limits, focusing on instantaneous speed and average speed.
Explanation of instantaneous speed using the analogy of observers O1 and O2 to illustrate the transition from average to instantaneous speed.
The indeterminate form 0/0 and its significance in calculus, highlighting the need to avoid this expression when finding instantaneous rates.
The method of exhaustion used by the Ancient Greeks to find areas under curves, as an early form of integral calculus.
The physical interpretation of the area under a curve, such as distance traveled when velocity is plotted against time.
The fundamental theorem of integral calculus, which reveals the deep relationship between differential and integral calculus.
The importance of the limit concept in calculus, including its role in finding tangents to curves and summing areas under curves.
The geometric series example to illustrate the concept of infinite sums and their finite results, challenging traditional notions of addition.
Zeno's paradoxes, particularly the Tortoise and the Hare, as a historical challenge to understanding the concept of infinity in mathematics.
The resolution of Zeno's paradox using the concept of infinite series and their summation to finite values.
The course's progression from basic concepts of functions and sets to more complex applications and techniques in calculus.
The significance of sets as the fundamental language of modern mathematics and their role in understanding functions.
The course's focus on applications of calculus in engineering and physics, moving from theoretical foundations to practical problem-solving.
The importance of understanding the basic definition of instantaneous rate of change and how it remains consistent throughout the course.
The exploration of infinite series as a concluding topic, addressing the challenge of summing an infinite number of terms.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: