Unit IV: Lec 1 | MIT Calculus Revisited: Single Variable Calculus
TLDRThis MIT OpenCourseWare lecture delves into the origins and fundamentals of integral calculus, tracing its roots back to ancient Greece with the 'Method of Exhaustion' for calculating areas. Professors illustrate the technique using the area under a parabolic curve as an example, demonstrating how to approximate areas with increasing precision. The lecture highlights the aesthetic simplicity of Greek methods and sets the stage for the profound relationship between integral and differential calculus, which will be explored in subsequent sessions.
Takeaways
- 📚 The lecture introduces integral calculus, which has its roots in ancient Greece and is distinct from differential calculus.
- 🔍 The historical context highlights that integral calculus was practiced as early as 600 BC, predating differential calculus by over 2000 years.
- 📈 The lecture focuses on 'Two-dimensional Area', the foundational concept of integral calculus, which involves calculating areas in plane regions.
- 📝 The 'Axioms for Area' are introduced as the basic properties of area that the ancient Greeks used to develop the 'Method of Exhaustion'.
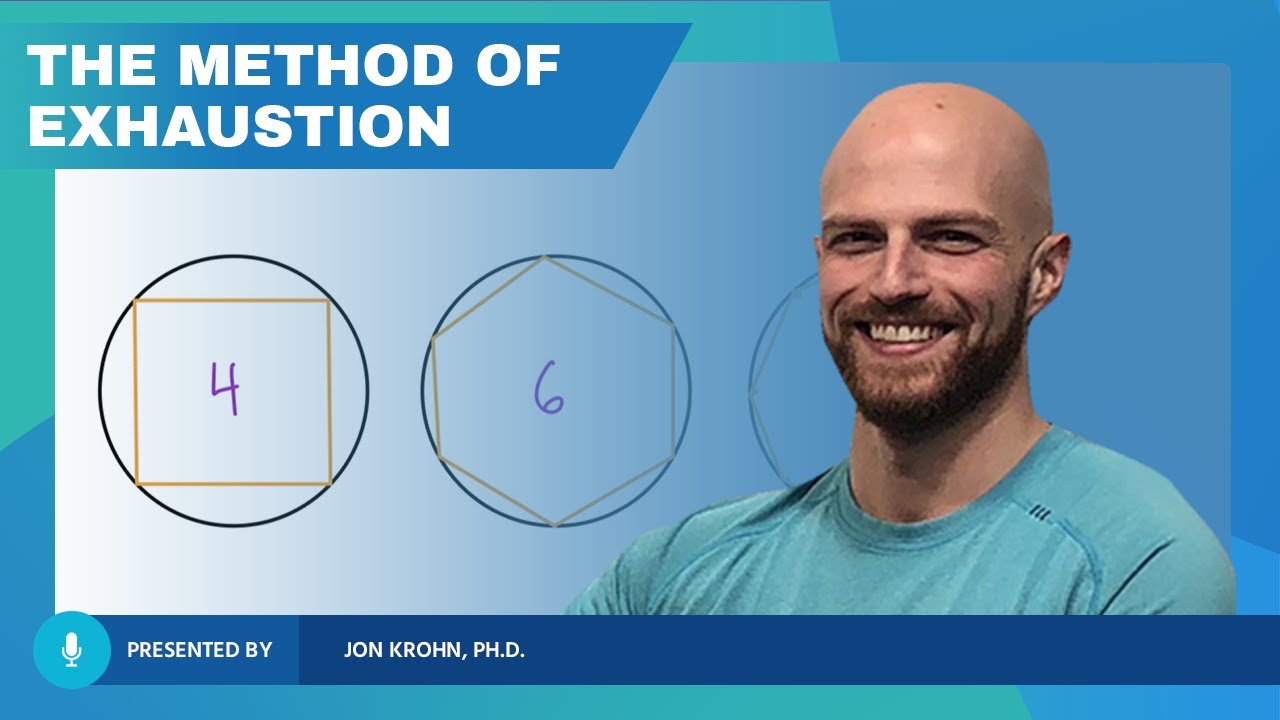
- 🔑 The 'Method of Exhaustion' is explained as a technique for finding areas by approximating them with rectangles, which is foundational to integral calculus.
- 📉 The process involves creating upper and lower bounds for the area of a region by inscribing and circumscribing rectangles around a given shape.
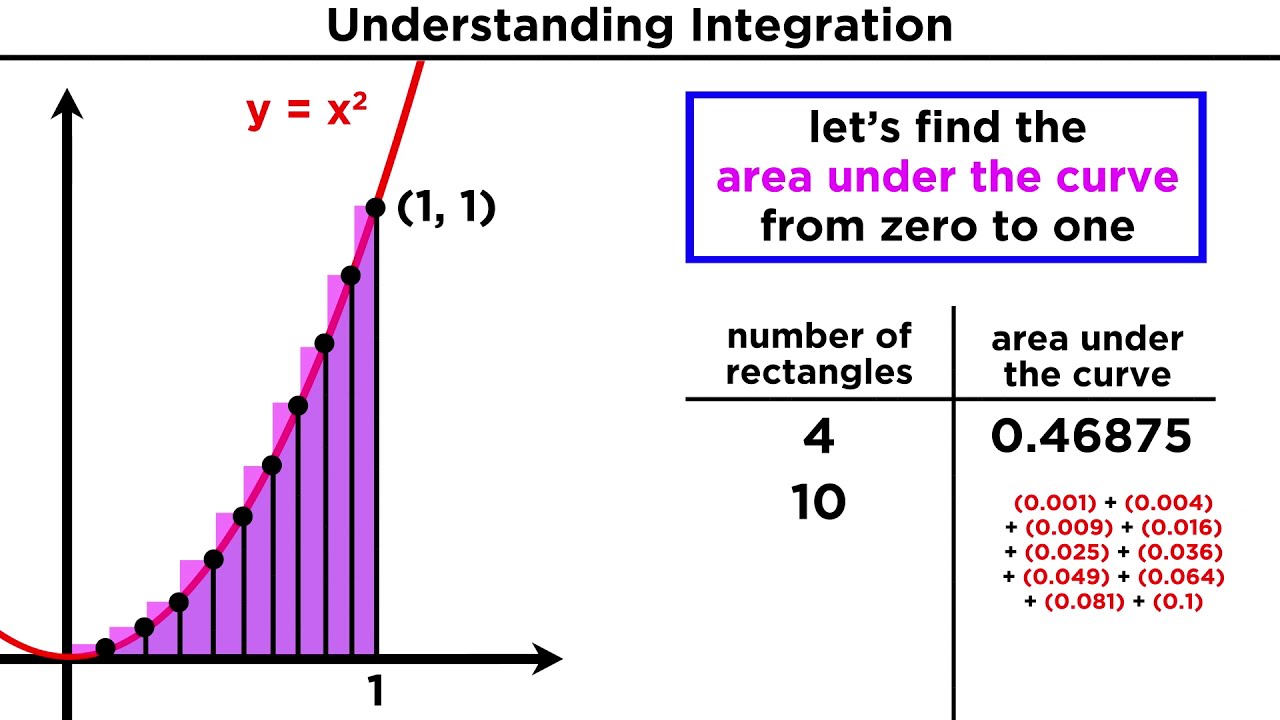
- 📝 An example is provided using the area under the curve y = x^2, bounded by the x-axis and the line x = 1, to illustrate the method of exhaustion.
- 🔬 The importance of the limits of upper and lower bounds as 'n' approaches infinity is emphasized to find the exact area, showcasing the convergence of these bounds.
- 📊 The concept of trapezoidal approximations is briefly introduced as an alternative method to estimate areas under curves, providing a quicker but approximate result.
- 📐 The script discusses the generalization of the method of exhaustion for any positive, continuous, and non-decreasing function, expanding its applicability.
- 💡 The lecture concludes by emphasizing the independence of integral calculus from differential calculus and hints at the profound relationship between the two in future lectures.
Q & A
What is the historical context of integral calculus mentioned in the script?
-The script mentions that integral calculus has its roots in ancient Greece around 600 BC, beginning with the study of area, and it was practiced by the ancient Greeks more than 2000 years before differential calculus started in 1680 AD with Sir Isaac Newton.
What is the significance of the 'Axioms for Area' in the script?
-The 'Axioms for Area' are three basic properties of area that were used by the ancient Greeks to find areas in general. They include: 1) the area of a rectangle is the base times the height, 2) the area of a contained region is less than or equal to that of the containing region, and 3) the area of the whole equals the sum of the areas of the parts.
Can you explain the 'Method of Exhaustion' as described in the script?
-The 'Method of Exhaustion' is a technique invented by the ancient Greeks for finding areas. It involves squeezing the region whose area is to be found between two networks of rectangles. By knowing the area of rectangles, the method allows for the calculation of the area of the entire region by summing the areas of the constituent parts.
What is the specific problem that Archimedes dealt with as mentioned in the script?
-Archimedes dealt with finding the area of parabolic segments, which is an example of a problem that can be tackled using the method of exhaustion.
How does the script illustrate the concept of an upper and lower bound in the context of the method of exhaustion?
-The script uses the example of a region bounded by the curve y=x^2, the x-axis, and the line x=1. It shows that the area of this region is less than the area of a rectangle containing it (upper bound) and greater than the area of a rectangle inscribed within it (lower bound), thus providing an initial estimate of the area.
What is the significance of the upper and lower bounds ('U sub n' and 'L sub n') in the method of exhaustion?
-The upper and lower bounds ('U sub n' and 'L sub n') are estimates of the area of the region that are derived by summing the areas of circumscribed and inscribed rectangles, respectively. As 'n' (the number of partitions) increases, these bounds converge to the same limit, which is the exact area of the region.
How does the script explain the convergence of 'U sub n' and 'L sub n' to the same limit?
-The script explains that for each partition, the difference between 'U sub n' and 'L sub n' is '1/n'. As 'n' approaches infinity, this difference approaches zero, indicating that the two bounds converge to the same limit.
What is the practical application of the method of exhaustion in terms of finding the area under a curve?
-The method of exhaustion allows for the exact calculation of the area under a curve by providing a way to estimate this area with increasing precision. It involves partitioning the region under the curve into smaller parts and summing the areas of these parts, which converge to the actual area as the partition size decreases.
Can you provide an example of how the script uses the sum of squares to simplify the calculation of 'U sub n'?
-The script uses the formula for the sum of the first 'n' squares, which is 'n(n + 1)(2n + 1)/6', to simplify the calculation of 'U sub n'. By dividing this sum by 'n cubed' and simplifying, it shows that 'U sub n' approaches 1/3 as 'n' goes to infinity.
What is the script's final point about the relationship between differential and integral calculus?
-The script concludes by noting that while the study of area (integral calculus) can be done independently of differential calculus, there is a remarkable and beautiful relationship between the two, which will be explored in the next lecture.
Outlines
📚 Introduction to Integral Calculus and Its Historical Roots
The script begins with an introduction to integral calculus, highlighting its origins dating back to ancient Greece around 600 BC. It emphasizes the study of two-dimensional area, which is foundational to integral calculus. The lecture, titled 'Calculus Revisited Revisited,' aims to explore integral calculus independently of differential calculus, noting the historical precedence of integral calculus by over 2000 years. The professor introduces the 'Axioms for Area,' which are fundamental in understanding how to calculate areas, especially using the 'Method of Exhaustion' invented by the ancient Greeks. This method involves approximating the area of a shape by 'squeezing' it between rectangles whose areas are known, leading to the development of integral calculus as we know it today.
📐 The Method of Exhaustion: Squeezing the Area Under a Curve
This paragraph delves into the application of the Method of Exhaustion to calculate the area under a curve. It uses the example of finding the area of a region bounded by the curve y = x^2, the x-axis, and the vertical lines x = 0 and x = 1. The process involves creating rectangles that either contain or are contained within the region of interest, thus providing upper and lower bounds for the area. The method refines these bounds by partitioning the region into more parts, leading to a better approximation. The paragraph explains how by increasing the number of partitions (denoted by 'n'), the approximation becomes more accurate, ultimately approaching the true area of the region under the curve.
🔍 Upper and Lower Bounds in the Method of Exhaustion
The script continues to explain the concept of upper and lower bounds in the context of the Method of Exhaustion. It describes how to calculate these bounds by summing the areas of circumscribed and inscribed rectangles within the region 'R'. The paragraph introduces 'U sub n' as the upper bound and 'L sub n' as the lower bound, which are functions of the number of partitions 'n'. The goal is to find the limit of these bounds as 'n' approaches infinity, which should converge to the same value, thus determining the exact area of the region 'R'. The paragraph also illustrates how the difference between the upper and lower bounds decreases as 'n' increases, ensuring a more precise approximation of the area.
📉 Convergence of Upper and Lower Bounds to Determine the Area
The paragraph discusses the convergence of the upper and lower bounds to the same limit, which is key to finding the exact area of a region. It explains that as 'n' approaches infinity, the difference between 'U sub n' and 'L sub n' approaches zero, indicating that these bounds converge to the same value. The area 'A sub R' of the region 'R' is therefore determined to be this common limit. The script provides a numerical example with 'n' equal to 1,000, showing how close the approximations are to the exact value and demonstrating the method's effectiveness. It also touches on the historical approximation of pi using the fraction 22/7, drawing a parallel to the method of exhaustion's approach to refining estimates.
🔢 Mathematical Interpretation of Upper Bounds and Their Limit
This section provides a mathematical interpretation of the upper bounds 'U sub n' and their behavior as 'n' increases. It shows that 'U sub n' is greater than 1/3 for every 'n' and decreases as 'n' gets larger, with the limit as 'n' approaches infinity being 1/3. The script uses sigma notation to express the sum of squares and manipulates it to reveal the structure of 'U sub n'. It emphasizes that no matter how large 'n' is, 'U sub n' will always be greater than 1/3, and as 'n' approaches infinity, 'U sub n' gets arbitrarily close to 1/3, confirming the convergence of the bounds to the exact area.
📌 Lower Bounds and Their Convergence to the Same Limit
The paragraph examines the lower bounds 'L sub n' and their convergence to the same limit as the upper bounds. It presents a formula for 'L sub n' that mirrors the structure of 'U sub n' but with subtraction instead of addition. The script explains that 'L sub n' is less than 1/3 for each 'n', but as 'n' increases, 'L sub n' also increases, converging to 1/3 as 'n' approaches infinity. The importance of both upper and lower bounds converging to the same value is highlighted, ensuring that the area of the region 'R' is precisely the common limit of both sequences.
📘 Generalization of the Method of Exhaustion for Any Positive Continuous Function
The script generalizes the method of exhaustion for any positive, continuous, and non-decreasing function 'f' on the interval 'a' to 'b'. It describes the process of partitioning the interval into 'n' equal parts and constructing upper and lower bounds 'U sub n' and 'L sub n' by choosing the highest and lowest points in each partition to form rectangles. The paragraph explains that the sums formed by these rectangles, using sigma notation, also converge to the area 'A sub R' of the region under the curve. The importance of the difference between 'U sub n' and 'L sub n' approaching zero as 'n' approaches infinity is reiterated, ensuring the convergence to the exact area.
📌 Trapezoidal Approximations as an Alternative to the Method of Exhaustion
This paragraph introduces trapezoidal approximations as an alternative method to estimate the area under a curve, using the example of the curve y = x^2. It explains that by dividing the region into parts and replacing the curve's arc with straight line segments (chords), one can calculate the area of the resulting trapezoids to approximate the area under the curve. The script demonstrates that even with just a few subdivisions, the trapezoidal approximation can be quite close to the exact area, as shown with numerical examples. It also notes that this approximation is an over-approximation because the chords lie above the arc of the curve.
📝 Conclusion on the Method of Exhaustion and Its Historical Significance
The final paragraph concludes the lecture on the method of exhaustion, emphasizing its historical significance and the intellectual achievement of the ancient Greeks in developing this technique. It acknowledges the difficulty of the method but encourages students to appreciate its elegance and to attempt to understand it through exercises. The script also touches on the importance of continuity for finding areas and the possibility of dealing with piecewise continuous functions. It hints at the relationship between differential and integral calculus to be explored in future lectures and thanks the Gabriella and Paul Rosenbaum Foundation for funding the video's publication, encouraging donations to support MIT OpenCourseWare.
Mindmap
Keywords
💡Integral Calculus
💡Creative Commons License
💡MIT OpenCourseWare
💡Two-dimensional Area
💡Axioms for Area
💡Method of Exhaustion
💡Differential Calculus
💡Archimedes
💡Trapezoidal Approximation
💡Piecewise Continuous
💡Net Area
Highlights
Integral calculus has its roots in ancient Greece, beginning with the study of area around 600 BC.
Integral calculus can be studied independently of differential calculus, despite being taught after it.
Differential calculus began much later in 1680 AD with Sir Isaac Newton.
The ancient Greeks used three simple properties of area, known as 'Axioms for Area', to develop the 'Method of Exhaustion'.
The 'Method of Exhaustion' involves finding the area of a region by squeezing it between networks of rectangles.
Archimedes used the 'Method of Exhaustion' to find the area of parabolic segments between 300 to 600 BC.
The method provides an upper and lower bound for the area of a region, which can be refined by increasing the number of subdivisions.
The area of a region bounded by a curve and the x-axis can be approximated by the areas of rectangles inscribed or circumscribed around it.
As the number of subdivisions increases, the approximation of the area converges to the actual area of the region.
The sum of the areas of the first 'n' squares can be found using the formula 'n(n + 1)(2n + 1)/6'.
The method of exhaustion can provide an exact area calculation, but it can be difficult to find the limit in practice.
Trapezoidal approximations offer a faster method for estimating the area under a curve compared to the method of exhaustion.
The method of exhaustion is applicable to piecewise continuous functions, even if they have jump discontinuities.
The method can be generalized to use any point within a partition interval to estimate the area, not just the endpoints.
The concept of net area allows for the calculation of areas where the function is negative, by considering the signed area.
The study of integral calculus is distinct from differential calculus and can be understood independently.
Transcripts
Browse More Related Video

Unit IV: Lec 2 | MIT Calculus Revisited: Single Variable Calculus
What is Integration? Finding the Area Under a Curve

Lec 21 | MIT 18.01 Single Variable Calculus, Fall 2007
What Integral Calculus Is — Topic 85 of Machine Learning Foundations
The Method of Exhaustion – Topic 44 of Machine Learning Foundations

Preface | MIT Calculus Revisited: Single Variable Calculus
5.0 / 5 (0 votes)
Thanks for rating: