Introductory Calculus: Oxford Mathematics 1st Year Student Lecture
TLDRIn this introductory Calculus lecture, the professor, Dan Ciubotaru, outlines the course structure, covering differential equations, integration techniques, and calculus of functions in two variables. He emphasizes the practical applications of these concepts in physical sciences and engineering, providing examples such as Newton's second law and electrical circuits. The lecture also reviews integration methods, including integration by parts and separable equations, highlighting their importance in solving more complex mathematical problems.
Takeaways
- 📘 The course introduces Calculus with a focus on practical information, syllabus, and coverage including differential equations and integration.
- 🗓 The course consists of 16 lectures, with lecture notes available online, authored by Cath Wilkins, and taught by Dan Ciubotaru.
- 📆 The lectures are scheduled for Mondays and Wednesdays at 10am, with an additional four hours allocated for tutorials in the college.
- 📚 Students are provided with eight problem sheets, with the first two available online, to be covered in college tutorials.
- 📈 The first half of the course is dedicated to differential equations, including ordinary (ODEs) and partial (PDEs) differential equations.
- 🔍 The course will explore examples of differential equations from physical sciences, such as mechanics and electrical circuits, demonstrating their applications.
- 📊 The latter part of the course will cover line and double integrals, allowing the computation of arc lengths of curves and areas of regions in the plane or surfaces.
- 🔧 Introduction to multivariable calculus will be provided, including gradient, normal vectors, Taylor's theorem in two variables, critical points, and Lagrange multipliers.
- 🔗 The course has significant interaction with other preliminary courses, such as multivariable calculus, dynamics, and PDEs, as well as analysis.
- 📖 A recommended textbook for the course is 'Mathematical Methods in Physical Sciences' by Mary Boas, which is concise and contains examples from various fields.
- 📝 The course is mandatory and considered a foundational subject, with further applied mathematics options available in Part A of the curriculum.
Q & A
What is the main focus of the course Introduction to Calculus?
-The main focus of the course is to cover differential equations, including both ordinary and partial differential equations, as well as integration techniques and calculus of functions in two variables.
How many lectures are there in total for the Introduction to Calculus course?
-There are 16 lectures in total for the Introduction to Calculus course.
Who are the lecture notes for the course written by?
-The lecture notes are written by Cath Wilkins, who taught the course for a few years until last year.
What is the name of the lecturer for the Introduction to Calculus course?
-The lecturer's name is Dan Ciubotaru.
On which days and time will the lectures for the Introduction to Calculus course take place?
-The lectures will take place on Mondays and Wednesdays at 10 am.
How many problem sheets will students have to complete for the course?
-Students will have eight problem sheets to complete for the course.
Which book is recommended for further reading and examples in the course?
-The book 'Mathematical Methods in Physical Sciences' by Mary Boas is recommended for further reading and examples.
What is the significance of differential equations in applied mathematics?
-Differential equations are significant in applied mathematics as they appear in various fields such as mechanics, engineering, and electrical circuits, and are essential for modeling and solving real-world problems.
How does the course Introduction to Calculus interact with other preliminary courses?
-The course interacts with other preliminary courses such as multivariable calculus, dynamics, and analysis, providing foundational knowledge and techniques that are further developed and applied in these courses.
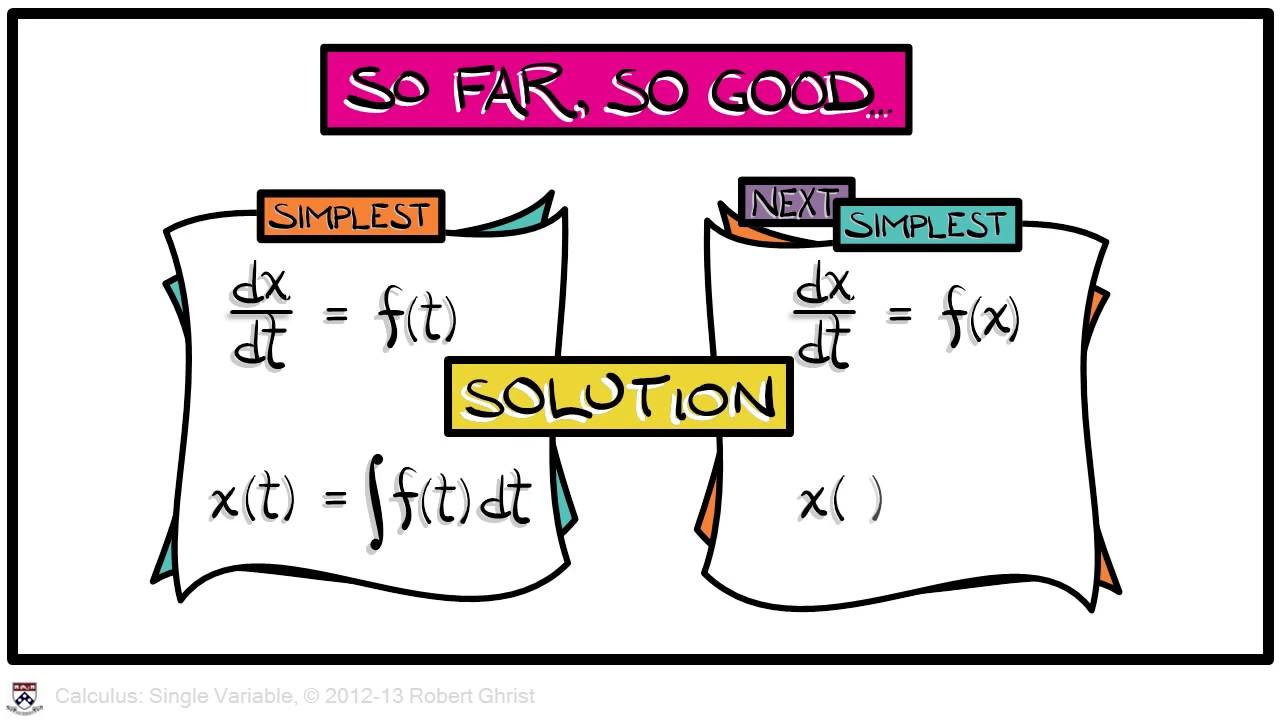
What is the simplest kind of ordinary differential equation (ODE) discussed in the script?
-The simplest kind of ODE discussed is of the form dy/dx = f(x), which can be solved by direct integration.
What is the method used to solve the integral of the product of two functions, x^2*sin(x)?
-The method used to solve the integral of x^2*sin(x) is integration by parts.
How can you check if a differential equation is separable?
-A differential equation is separable if it can be written in the form dy/dx = a(x)*b(y), where a(x) is a function of x only and b(y) is a function of y only.
Outlines
📚 Introduction to Introductory Calculus
The lecturer, Dan Ciubotaru, begins the first lecture of Introductory Calculus by sharing practical information about the course structure, including the number of lectures, availability of lecture notes online, and tutorial schedules. He introduces himself and sets expectations for the course difficulty, suggesting that it may start off easy but will progress in complexity. The syllabus is briefly introduced, with a focus on differential equations from physical sciences and integration techniques. The lecturer also mentions the textbook 'Mathematical Methods in Physical Sciences' by Mary Boas as a recommended resource.
🔍 Syllabus Overview and Integration
The lecturer continues by detailing the syllabus, emphasizing the first half of the course will focus on differential equations, including ordinary and partial differential equations (ODEs and PDEs). He provides examples of how these equations arise in various fields, such as mechanics and electrical circuits. The second half of the course will cover line and double integrals, leading to the introduction of multivariable calculus, including topics like gradient, normal vectors, Taylor's theorem, critical points, and Lagrange multipliers. The lecturer also discusses the interconnection between this course and others in the mathematics program, highlighting the relevance of the material to future studies.
🌐 Applications of Differential Equations
The lecturer delves into the applications of differential equations (DEs), defining ordinary differential equations (ODEs) and providing examples from mechanics and electrical circuits. He explains how Newton's second law leads to a second-order differential equation and how an RLC electrical circuit gives rise to a second-order inhomogeneous equation with constant coefficients. The lecturer also poses an exercise for the students to formulate a differential equation for the decay of radioactive material.
📝 Integration Techniques
The lecturer reviews integration techniques, focusing on integration by parts, which is derived from the product rule. He works through examples to demonstrate the process, including integrating functions like x^2sin(x) and 2x - 1 times the natural log of (x^2 + 1). The lecturer emphasizes the importance of these techniques for solving differential equations and encourages students to practice more if they are not fully comfortable with the examples provided.
🔄 Recursive Formulas and Separable Equations
The lecturer introduces the concept of recursive formulas for solving certain types of integrals that do not simplify in a single step. He provides an example involving the integral of cosine to the power of n times x, leading to a recursive formula for I(n) in terms of I(n-1) and I(n-2). The lecturer then transitions to discussing separable differential equations, showing how to solve them through a step-by-step example involving the equation x*(y^2 - 1) + y*(x^2 - 1) = 0, and highlights the importance of considering all possible solutions, including those where the denominator might be zero.
🎓 Conclusion and Future Lectures
In the concluding paragraph, the lecturer summarizes the content covered in the first lecture and sets the stage for future lectures, where more differential equations will be explored. He reminds students of the importance of understanding integration techniques for solving these equations and encourages them to review the material and prepare for the next session.
Mindmap
Keywords
💡Introductory Calculus
💡Differential Equations
💡Integration
💡Lectures and Tutorials
💡Syllabus
💡Ordinary Differential Equations (ODEs)
💡Partial Differential Equations (PDEs)
💡Integration by Parts
💡Problem Sheets
💡Textbook
💡Multivariable Calculus
Highlights
Introduction to Introductory Calculus course and its structure, including practical information and the syllabus.
Course will cover differential equations, integration, and calculus of functions in two variables.
Lecture notes and reading materials are available online, with a recommended book by Mary Boas for additional resources.
The first half of the course focuses on differential equations, including ordinary and partial differential equations (ODEs and PDEs).
Differential equations have practical applications in physical sciences, mechanics, and engineering, such as Newton's second law and electrical circuits.
Integration techniques, such as integration by parts, are essential for solving differential equations.
The course will also cover line and double integrals, which are useful for calculating arc lengths of curves and areas of regions in the plane or surfaces.
Calculus of functions in two variables will serve as an introduction to multivariable calculus, including gradient, normal vectors, Taylor's theorem, critical points, and Lagrange multipliers.
There is significant interaction between this course and other preliminary courses, such as multivariable calculus, dynamics, and analysis.
The course is mandatory and has many applied mathematics options, making it a foundational subject for further studies.
The simplest kind of ODE is dy/dx = f(x), which can be solved by direct integration.
Integration by parts is a useful technique derived from the product rule and can be applied to various functions.
Recursive formulas can be found for certain types of integrals that do not simplify easily, such as cosine to the power of n times x.
Separable differential equations can be simplified by dividing by a function of y only and integrating both sides.
The general solution to a separable differential equation is found by integrating and applying logarithmic properties.
Care must be taken when dividing by functions in y to ensure that the solution includes all possible values, including zero.
The course will explore various techniques for solving differential equations, emphasizing the combination of science and art in finding solutions.
The importance of understanding integration techniques is emphasized for successfully solving differential equations.
The lecturer introduces himself as Dan Ciubotaru and sets the expectation for the course's difficulty and progression.
Transcripts
Browse More Related Video
Calculus Chapter 3 Lecture 17 Indefinite Integrals

Lec 30 | MIT 18.01 Single Variable Calculus, Fall 2007

What Math Classes Do Engineers (and Physics Majors) Take?

LIMITS CALCULATOR TECHNIQUES - DIFFERENTIAL CALCULUS | ENGINEERING BOARD EXAM REVIEW | YU JEI ABAT

Math1325 Lecture 13 6

Business Calculus - Math 1329 - Section 5.1 - Indefinite Integration & Differential Equations
5.0 / 5 (0 votes)
Thanks for rating: