Reference Angles Trigonometry, In Radians, Unit Circle - Evaluating Trig Functions

The Organic Chemistry Tutor
8 Nov 201619:25
EducationalLearning
32 Likes 10 Comments

TLDRThis video script explains how to find reference angles in different quadrants. It covers angles in quadrants one to four, negative angles, and angles in radians. Examples demonstrate calculating reference angles and their importance in solving trigonometry problems, especially using special right triangles like 30-60-90.

Takeaways
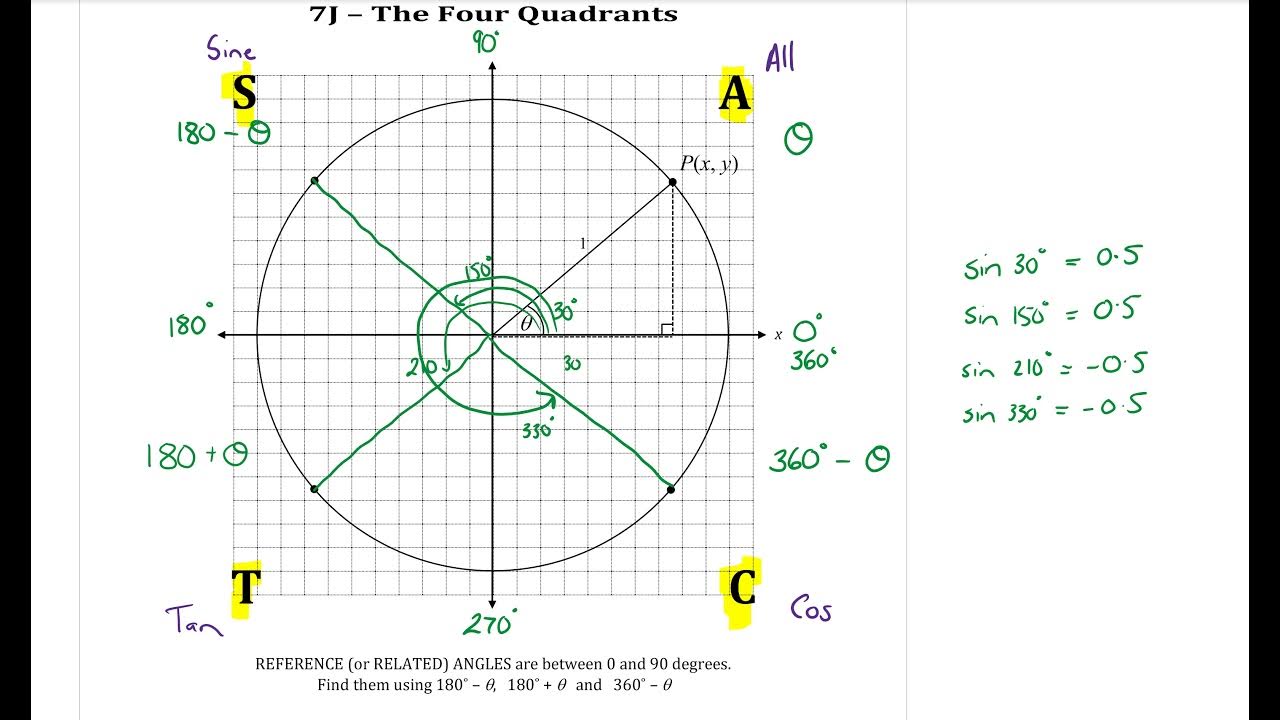
  • πŸ“š Reference angles are the acute angles formed between the terminal side of an angle and the x-axis in a coordinate plane.
  • 🧭 Quadrant 1 angles are between 0 and 90 degrees, and their reference angles are equal to the angle itself.
  • πŸ“ Quadrant 2 angles are between 90 and 180 degrees, with reference angles calculated as 180 minus the angle.
  • πŸ“‰ Quadrant 3 angles are between 180 and 270 degrees, and their reference angles are the angle minus 180.
  • πŸ“Š Quadrant 4 angles are between 270 and 360 degrees, with reference angles found by subtracting the angle from 360.
  • πŸ“ˆ Example given: An angle of 210 degrees in Quadrant 3 has a reference angle of 30 degrees, calculated as 210 - 180.
  • πŸ“ For negative angles, find a coterminal angle between 0 and 360 degrees to determine the reference angle.
  • πŸ”’ Angles larger than 360 degrees can be reduced to a coterminal angle within the 0 to 360 range to find the reference angle.
  • πŸ“² When given an angle in radians, convert it to degrees and find the reference angle as you would with degree measures.
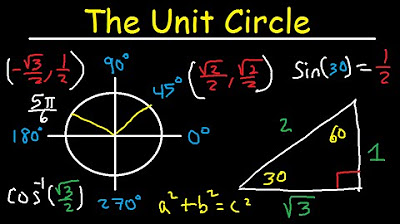
  • πŸ”‘ The reference angle is crucial for evaluating trigonometric functions without a calculator, especially using special right triangles like the 30-60-90 triangle.
  • πŸ“‰ The sign of trigonometric functions depends on the quadrant in which the angle lies, and reference angles help determine these signs.
Q & A

  • What are the four quadrants in a coordinate system?

    -The four quadrants in a coordinate system are: Quadrant 1 (between 0 and 90 degrees), Quadrant 2 (between 90 and 180 degrees), Quadrant 3 (between 180 and 270 degrees), and Quadrant 4 (between 270 and 360 degrees).

  • What is a reference angle?

    -A reference angle is the acute angle formed between the terminal side of an angle and the x-axis. It is always between 0 and 90 degrees.

  • How do you find the reference angle of an angle in Quadrant 1?

    -The reference angle of an angle in Quadrant 1 is equal to the angle itself, as it is already an acute angle between 0 and 90 degrees.

  • What is the formula to find the reference angle of an angle in Quadrant 2?

    -The reference angle of an angle in Quadrant 2 is found by subtracting the angle from 180 degrees (180 - angle).

  • How do you determine the reference angle for an angle in Quadrant 3?

    -The reference angle for an angle in Quadrant 3 is calculated by subtracting the angle from 180 degrees (180 - angle).

  • What is the formula to find the reference angle of an angle in Quadrant 4?

    -The reference angle of an angle in Quadrant 4 is found by subtracting the angle from 360 degrees (360 - angle).

  • How do you find the reference angle of an angle that is 210 degrees?

    -Since 210 degrees is in Quadrant 3, the reference angle is calculated by subtracting 180 from 210, which gives 30 degrees.

  • What is the reference angle of an angle that is 160 degrees?

    -Since 160 degrees is in Quadrant 2, the reference angle is found by subtracting 160 from 180, resulting in 20 degrees.

  • How do you find the reference angle of an angle that is 314 degrees?

    -Since 314 degrees is in Quadrant 4, the reference angle is calculated by subtracting 314 from 360, which gives approximately 46 degrees.

  • What is the reference angle of an angle in radians, such as 5Ο€/3?

    -The reference angle of an angle in radians like 5Ο€/3 is simply Ο€/3, as the reference angle is the same regardless of the quadrant the angle is in.

  • Why are reference angles important in solving trigonometry problems?

    -Reference angles are important because they help in evaluating trigonometric functions without a calculator by using known values from special right triangles, such as the 30-60-90 triangle.

  • How do you find the reference angle of a negative angle?

    -To find the reference angle of a negative angle, you find a coterminal angle between 0 and 360 degrees by adding or subtracting multiples of 360 to the given angle.

  • What is the reference angle for an angle larger than 360 degrees?

    -To find the reference angle for an angle larger than 360 degrees, you find a coterminal angle between 0 and 360 degrees by subtracting multiples of 360 from the given angle.

  • How do you convert an angle in radians to degrees?

    -To convert an angle in radians to degrees, multiply the radian measure by 180 and divide by Ο€ (180Β°/Ο€).

  • What is the reference angle of an angle in Quadrant 1 in radians?

    -The reference angle of an angle in Quadrant 1 in radians is equal to the angle itself, as it is already between 0 and Ο€/2 radians.

Outlines
00:00
πŸ“š Understanding Reference Angles and Quadrants

This paragraph introduces the concept of reference angles and their relation to the four quadrants in a coordinate system. It explains that an angle in the first quadrant has the same reference angle as its measure, while angles in other quadrants have reference angles calculated by subtracting from 180 degrees (for quadrant two), 180 degrees (for quadrant three), or adding to 360 degrees (for quadrant four). The paragraph also provides examples of how to find reference angles for angles in different quadrants, such as 210 degrees in quadrant three and 160 degrees in quadrant two.

05:03
πŸ“ Calculating Reference Angles for Various Angles

This paragraph continues the discussion on reference angles, focusing on how to calculate them for angles in different quadrants and for negative and large angles. It explains that for negative angles, you find a coterminal angle between 0 and 360 degrees by adding or subtracting 360. For angles larger than 360 degrees, you find a coterminal angle by subtracting multiples of 360. The paragraph also covers how to find reference angles for angles given in radians, such as 5Ο€/3, and how to convert these angles to degrees for easier calculation.

10:07
πŸ€” Converting Radians to Degrees and Finding Reference Angles

This paragraph delves into the process of converting angles from radians to degrees and using this conversion to find reference angles. It provides examples of how to convert negative angles and angles larger than 2Ο€ (360 degrees) into a coterminal angle within the range of 0 to 360 degrees. The paragraph also discusses the importance of reference angles in solving trigonometry problems, particularly when evaluating trigonometric functions without a calculator.

15:09
πŸ” Applying Reference Angles to Trigonometric Functions

The final paragraph highlights the practical application of reference angles in evaluating trigonometric functions. It uses the example of finding the sine of 150 degrees by relating it to the sine of 30 degrees, which is a reference angle in a 30-60-90 triangle. The paragraph also explains how to find the tangent of an angle like 5Ο€/3 by first determining its reference angle and then using the properties of the 30-60-90 triangle. This demonstrates the utility of reference angles in simplifying trigonometric calculations.

Mindmap
Keywords
πŸ’‘Reference Angle
A reference angle is the acute angle formed between a line and the x-axis in a standard position. It is a fundamental concept in trigonometry, used to determine the values of trigonometric functions for any angle by relating them to their corresponding acute angles. In the video, reference angles are calculated for various quadrants to help find the values of trigonometric functions without a calculator. For example, the reference angle for an angle in quadrant three is found by subtracting the angle from 180 degrees.
πŸ’‘Quadrants
Quadrants are the four equal divisions of the coordinate plane by the x-axis and y-axis. Each quadrant has a specific range of angles: quadrant one (0 to 90 degrees), quadrant two (90 to 180 degrees), quadrant three (180 to 270 degrees), and quadrant four (270 to 360 degrees). The video discusses how the reference angle is determined based on the quadrant in which an angle lies, which is crucial for understanding trigonometric functions.
πŸ’‘Acute Angle
An acute angle is an angle less than 90 degrees. In the context of the video, reference angles are always acute angles, as they are the angles formed between a line and the x-axis in a standard position. The video emphasizes that reference angles are used to simplify the evaluation of trigonometric functions by relating them to acute angles, such as in the case of an angle in quadrant one, where the reference angle is equal to the angle itself.
πŸ’‘Trigonometric Functions
Trigonometric functions are mathematical functions that relate the angles of a triangle to the lengths of its sides. In the video, the importance of reference angles is highlighted in evaluating trigonometric functions like sine and tangent. For instance, knowing the reference angle allows one to determine the sine of an angle in quadrant two by using the sine of its reference angle in quadrant one.
πŸ’‘Coterminal Angles
Coterminal angles are angles that share the same terminal side and therefore have the same trigonometric function values. The video explains how to find coterminal angles for angles outside the standard range of 0 to 360 degrees by adding or subtracting multiples of 360 degrees. This is crucial for evaluating trigonometric functions of angles in different quadrants, as shown in the example with a negative angle converted to a positive coterminal angle in quadrant three.
πŸ’‘Radians
Radians are a unit of angular measurement used in trigonometry, where one radian is the angle subtended at the center of a circle by an arc whose length is equal to the radius of the circle. The video discusses how to convert angles from radians to degrees and vice versa, which is essential for understanding trigonometric functions in different units. For example, the reference angle of an angle in radians is found by converting it to degrees and then applying the standard reference angle rules.
πŸ’‘Unit Circle
The unit circle is a circle with a radius of one, centered at the origin of the coordinate plane. It is used in trigonometry to define trigonometric functions and to find reference angles. The video mentions the unit circle in relation to angles in radians, such as pi/3, and how these angles can be converted to degrees to find their reference angles.
πŸ’‘30-60-90 Triangle
A 30-60-90 triangle is a special right triangle where the angles are 30 degrees, 60 degrees, and 90 degrees. The video uses this triangle to illustrate how to find the values of trigonometric functions for angles in different quadrants by relating them to the reference angles of the 30-60-90 triangle. For example, the sine of 150 degrees is equal to the sine of 30 degrees because they share the same reference angle.
πŸ’‘Sine Function
The sine function is a trigonometric function that relates the ratio of the opposite side to the hypotenuse in a right triangle. In the video, the sine function is used to demonstrate how reference angles help in evaluating trigonometric functions. For instance, the sine of an angle in quadrant two can be found by using the sine of its reference angle in quadrant one.
πŸ’‘Tangent Function
The tangent function is a trigonometric function that relates the ratio of the opposite side to the adjacent side in a right triangle. The video explains how the tangent function is evaluated using reference angles, such as in the case of an angle in quadrant four, where the tangent is negative. The video also uses the 30-60-90 triangle to find the tangent of an angle by relating it to the tangent of its reference angle.
Highlights

Introduction to reference angles and their importance in trigonometry.

Explanation of the four quadrants and their angle ranges.

How to find the reference angle in quadrant one, which is equal to the angle itself.

Calculating the reference angle in quadrant two by subtracting the angle from 180 degrees.

Determining the reference angle in quadrant three by subtracting 180 from the angle.

Finding the reference angle in quadrant four by subtracting the angle from 360 degrees.

Example of calculating the reference angle for 210 degrees located in quadrant three.

Graphical representation of the reference angle for 160 degrees in quadrant two.

Demonstration of the reference angle calculation for 314 degrees in quadrant four.

How to handle negative angles by finding coterminal angles between 0 and 360 degrees.

Dealing with angles larger than 360 by finding coterminal angles within the 0-360 range.

Conversion of angles in radians to degrees to find reference angles.

Explanation of reference angles for common values on the unit circle, such as pi/3 and pi/6.

How angles not commonly featured on the unit circle can be handled by converting to degrees.

Finding the reference angle for unusual angles in radians by converting to degrees.

The significance of reference angles in evaluating trigonometric functions without a calculator.

Using the 30-60-90 triangle to evaluate sine and tangent of reference angles.

Practical example of finding sine of 150 degrees using the reference angle of 30 degrees.

Explanation of how to evaluate tangent of an angle in quadrant four using the reference angle.

Final thoughts on the importance of reference angles in solving trigonometry problems.

Transcripts

Browse More Related Video

How To Find The Reference Angle In Radians and Degrees - Trigonometry

How To Use Reference Angles to Evaluate Trigonometric Functions

How To Find The Exact Values of Trig Functions

REFERENCE ANGLES || PRE-CALCULUS

Yr 10 Trigonometry 10 - The four quadrants

Unit Circle Trigonometry - Sin Cos Tan - Radians & Degrees

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Reference AnglesTrigonometry BasicsQuadrantsAcute AnglesAngle CalculationMath EducationGeometry ConceptsRadians to DegreesTrigonometric FunctionsUnit Circle