Yr 10 Trigonometry 10 - The four quadrants
TLDRIn this lesson, we explore the four quadrants of the coordinate plane, focusing on how angles are measured and their relationships. Starting from the x-axis at 0 degrees and moving counterclockwise, we discuss reference angles in each quadrant. The lesson highlights how the sine, cosine, and tangent functions vary in sign across the quadrants and introduces the mnemonic 'All Stations to Central' to remember these rules. Examples demonstrate calculating angles and determining their signs, using both the unit circle and special triangles for exact values.
Takeaways
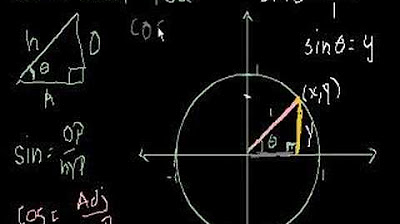
- 📚 The lesson discusses the concept of quadrants and reference angles in trigonometry, starting with a diagram showing the four quadrants and their respective angle measurements.
- 🔍 Angles are measured in an anti-clockwise direction, starting from the x-axis at 0 degrees, moving to 90 degrees at the top, 180 degrees on the left, 270 degrees at the bottom, and completing a full circle at 360 degrees.
- 🔢 Reference angles, or related angles, are introduced as a way to relate an acute angle in the first quadrant to angles in the other three quadrants.
- 📈 The relationship between an acute angle and its corresponding angles in other quadrants is demonstrated, showing how sine values remain the same but change signs depending on the quadrant.
- 📉 The script provides examples using sine of 30 degrees and 150 degrees, showing that their sine values are equal, illustrating the relationship between angles in different quadrants.
- 🌐 The mnemonic 'ASTC' is introduced to help remember the signs of sine, cosine, and tangent in each quadrant: All (all positive in the first quadrant), Sine (only sine positive in the second quadrant), Tangent (only tangent positive in the third quadrant), Cosine (only cosine positive in the fourth quadrant).
- 🚂 The phrase 'all stations to central' is used as a mnemonic to remember the order of ASTC as you move in an anti-clockwise direction around the circle.
- 📚 The script includes examples to practice determining the quadrant of an angle and whether sine, cosine, or tangent is positive or negative in that quadrant.
- 📐 The process of finding the reference angle for angles greater than 90 degrees is explained, showing how to relate these angles to their corresponding acute angles.
- 🔢 The script concludes with an example of finding the exact value of sine for an angle, demonstrating how to use a reference triangle to determine the sine value.
Q & A
What is the starting point for measuring angles in the diagram?
-Angles are measured starting from the x-axis at 0 degrees.
In which direction are angles measured in the diagram?
-Angles are measured in an anti-clockwise direction.
What is the relationship between an acute angle in the first quadrant and angles in the other quadrants?
-The sine of an acute angle in the first quadrant is the same as the sine of 180 minus that angle in the second quadrant, the sine of 180 plus that angle in the third quadrant, and the sine of 360 minus that angle in the fourth quadrant.
What happens to the sine value of an angle when it moves from the first quadrant to the other quadrants?
-In the second quadrant, the sine value remains the same. In the third and fourth quadrants, the sine value is negative.
What do the letters A, S, T, and C around the diagram represent?
-The letters A, S, T, and C stand for All, Sine, Tan, and Cos respectively, indicating which trigonometric functions are positive in each quadrant.
How is the angle in the third quadrant found?
-To find the angle in the third quadrant, you add the reference angle to 180 degrees.
What is the significance of the mnemonic 'All Stations to Central'?
-The mnemonic 'All Stations to Central' helps remember the order of the quadrants and which trigonometric functions are positive in each quadrant.
How do you determine if the sine, cosine, or tangent of an angle is positive or negative in a given quadrant?
-You use the mnemonic 'All Stations to Central' to determine that: in the first quadrant, all are positive; in the second, only sine is positive; in the third, only tangent is positive; and in the fourth, only cosine is positive.
What are the steps to find the reference angle for sine of 320 degrees?
-To find the reference angle for sine of 320 degrees, you subtract 320 from 360, resulting in a 40-degree reference angle. Since it's in the fourth quadrant, the sine value is negative.
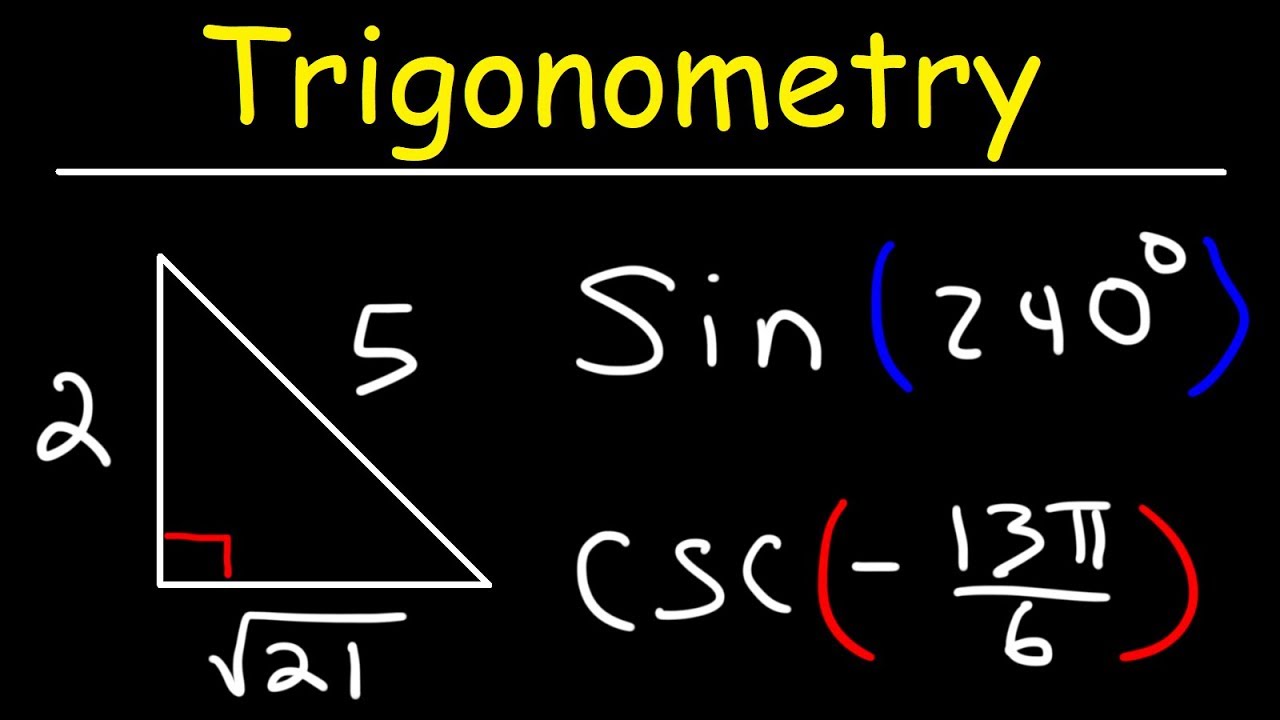
How do you find the exact value of sine 240 degrees using reference angles?
-First, find the reference angle by subtracting 180 from 240, which gives 60 degrees. Since it's in the third quadrant, sine 240 is negative. The exact value is found using the triangle with sine 60 degrees being √3/2, so sine 240 degrees is -√3/2.
Outlines
📐 Understanding the Four Quadrants and Reference Angles
The speaker introduces the concept of the four quadrants on a coordinate plane and explains how to measure angles starting from the x-axis at 0 degrees and moving counterclockwise to 360 degrees. They describe the relationships between acute angles in the first quadrant and corresponding angles in other quadrants, demonstrating this with the sine function. They show how sine of 30 degrees is equal to sine of 150 degrees, sine of 210 degrees is negative, and sine of 330 degrees is also negative.
🧮 Quadrant Rules for Sine, Cosine, and Tangent
This paragraph explains the mnemonic 'All Stations To Central' (ASTC) to remember which trigonometric functions are positive in each quadrant: all functions are positive in the first quadrant, only sine in the second, only tangent in the third, and only cosine in the fourth. The speaker uses examples like 330 degrees and 195 degrees to illustrate how to determine the positivity or negativity of sine, cosine, and tangent in different quadrants.
🔄 Calculating Reference Angles
The speaker describes how to find reference angles for given angles larger than 90 degrees. Using examples like sine of 320 degrees and cosine of 115 degrees, they demonstrate how to calculate the acute angle by subtracting from 360 or 180 degrees and checking the sign based on the quadrant. They explain the concept of the reference angle and its importance in trigonometric calculations.
📐 Using Reference Angles to Find Exact Values
This paragraph covers how to find exact trigonometric values using reference angles and special triangles. The speaker explains with an example of sine 240 degrees, showing how to determine the reference angle and then find the exact value using a 30-60-90 triangle. They emphasize the importance of considering the sign based on the quadrant, demonstrating the method step-by-step.
Mindmap
Keywords
💡Quadrants
💡Reference Angle
💡Sine (sin)
💡Cosine (cos)
💡Tangent (tan)
💡All Stations To Central (ASTC)
💡Angle Measurement
💡Acute Angle
💡Exact Value
💡Trigonometric Functions
Highlights
Introduction to the four quadrants and their respective angle measurements starting from 0 degrees on the x-axis and moving anti-clockwise.
Explanation of reference angles and their relationship with acute angles in the first quadrant.
Demonstration of how sine values remain the same for an acute angle and its corresponding angles in other quadrants, but with different signs.
Calculation of sine for 30 degrees and 150 degrees, showing they both equal 0.5, illustrating the relationship between angles in different quadrants.
Introduction of the mnemonic 'all stations to central' to remember the signs of sine, cosine, and tangent in each quadrant.
Detailed explanation of the mnemonic 'all stations to central' and its application to the first, second, third, and fourth quadrants.
Practice example: Determining the quadrant of an angle and stating whether sine, cosine, or tangent is positive or negative.
Analysis of 330 degrees, identifying it as being in the fourth quadrant and explaining the signs of trigonometric functions in this quadrant.
Explanation of how to find the reference angle for an angle in the third quadrant, using the example of 195 degrees.
Demonstration of converting an angle in the third quadrant to its reference angle and determining the sign of the trigonometric function.
Introduction to the process of writing trigonometric functions using their reference angles and including the correct sign.
Example of converting sine of 320 degrees to sine of its reference angle, including the correct sign based on the quadrant.
Explanation of how to find the reference angle for an angle in the second quadrant, using the example of 150 degrees.
Demonstration of converting cosine of 115 degrees to cosine of its reference angle, including the correct sign based on the quadrant.
Introduction to finding the tangent of an angle in the third quadrant, using the example of 203 degrees.
Explanation of how to find the reference angle for an angle in the third quadrant and determine the sign of the tangent function.
Extra question on finding the exact value of sine 240 degrees, demonstrating the process of finding the reference angle and its exact value.
Final summary of the process to find the exact value of a trigonometric function using reference angles and their properties in different quadrants.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: