Calculus 3: Lecture 11.7 Cylindrical and Spherical Coordinates
TLDRThis lecture transcript delves into the concepts of cylindrical and spherical coordinates, extending the understanding of polar coordinates. The instructor explains the representation of points in 3D space using (R, θ, Z) for cylindrical and (ρ, θ, φ) for spherical coordinates, emphasizing the formulas for converting between these systems and rectangular coordinates. The script includes practical examples and visual explanations, highlighting the ease of graphing cylinders and spheres using these coordinate systems. The lecture aims to ensure students can perform conversions and understand the mathematical principles behind these coordinate systems, with a touch of humor and emphasis on the importance of memorization for problem-solving.
Takeaways
- 📚 The script is an educational lecture on extending polar coordinates to cylindrical and spherical coordinate systems.
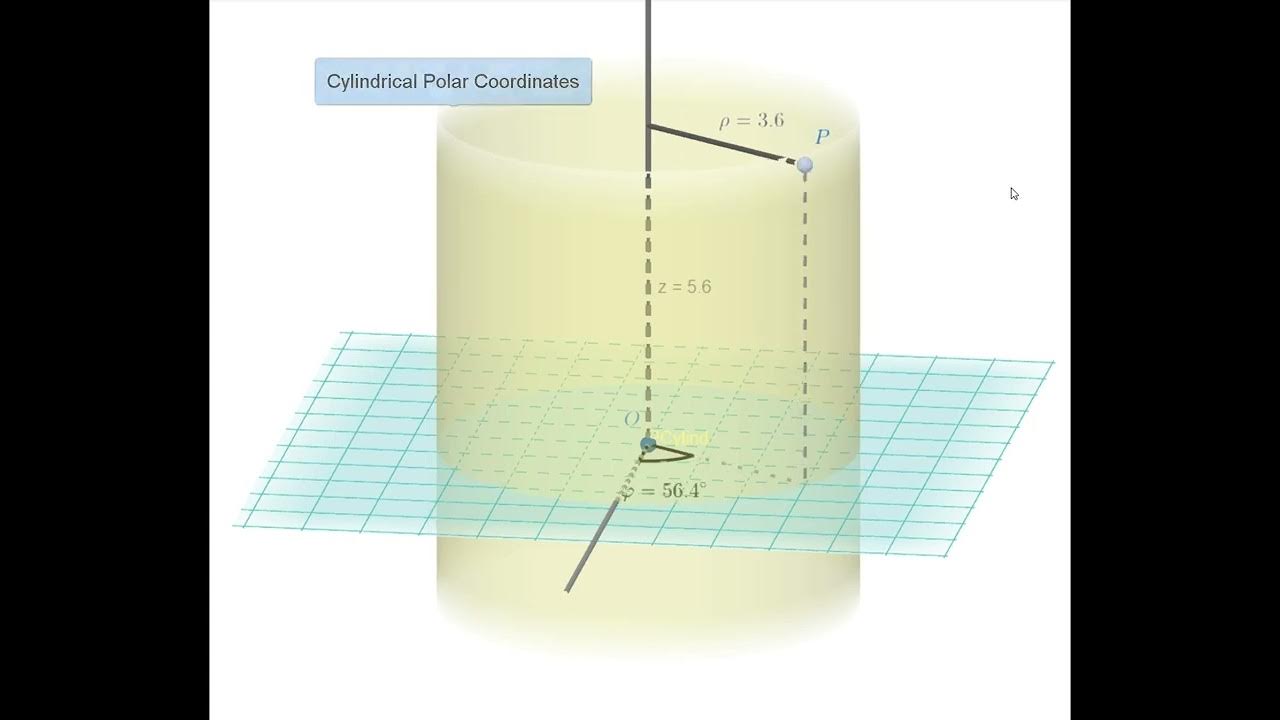
- 📐 Cylindrical coordinates are represented as (R, θ, Z), where R is the radial distance, θ is the azimuthal angle, and Z is the height above the xy-plane.
- 🔄 The conversion between cylindrical and rectangular (Cartesian) coordinates involves formulas that relate R, θ, and Z to x, y, and z coordinates.
- 📈 The lecturer emphasizes the importance of memorizing the formulas for cylindrical to rectangular conversion, as they are not provided on the formula sheet.
- 📉 The script includes a step-by-step example of converting a cylindrical coordinate to rectangular, highlighting the process and potential pitfalls.
- 🌐 Spherical coordinates are introduced as (ρ, θ, φ), with ρ being the radial distance from the origin, θ the azimuthal angle, and φ the polar angle from the positive z-axis.
- 🤔 The complexity of spherical coordinates is noted due to the additional angle φ, which is not present in cylindrical or polar coordinates.
- 📝 The formulas for converting between spherical and rectangular coordinates are provided, and their use is demonstrated through an example problem.
- 🧩 The script discusses the geometric interpretations of cylindrical and spherical coordinates, explaining how they relate to cylinders and spheres respectively.
- 🎨 A visual representation of a cylinder is attempted by the lecturer to aid understanding of cylindrical coordinates.
- ❓ The lecture includes an interactive element, where the lecturer encourages questions and clarifications from students to ensure understanding.
Q & A
What is the extension of polar coordinates discussed in the script?
-The extension of polar coordinates discussed in the script is cylindrical coordinates, which adds a Z coordinate to the polar system, resulting in a representation of points in the form R, θ, Z.
What is the significance of the Z coordinate in cylindrical coordinates?
-The Z coordinate in cylindrical coordinates represents the directed distance from the plane containing the polar representation to the point P, allowing for three-dimensional representation of points.
What is the formula for converting cylindrical to rectangular coordinates?
-The formulas for converting cylindrical coordinates (R, θ, Z) to rectangular coordinates (X, Y, Z) are X = R * cos(θ), Y = R * sin(θ), and Z remains the same.
How does the script describe the relationship between polar coordinates and circles?
-The script describes that in polar coordinates, varying the value of R while keeping θ constant results in circles being drawn, which is why adding a Z coordinate creates cylindrical shapes.
What is the projection of point P in the XY plane in the context of cylindrical coordinates?
-The projection of point P in the XY plane in cylindrical coordinates is the point (R * cos(θ), R * sin(θ), 0), which is the polar representation of the point when the Z component is ignored.
What is the formula for converting rectangular to cylindrical coordinates?
-The formulas for converting rectangular coordinates (X, Y, Z) to cylindrical coordinates (R, θ, Z) are R^2 = X^2 + Y^2, tan(θ) = Y / X, and Z remains the same.
What is the difference between cylindrical and spherical coordinates?
-Cylindrical coordinates use a single angle θ and a radius R with a Z coordinate, while spherical coordinates use two angles (θ and φ) and a radius ρ, providing a more complex three-dimensional representation.
What is the role of the angle θ in spherical coordinates?
-In spherical coordinates, θ is the angle from the positive z-axis to the line segment OP, where P is the point in space and O is the origin.
What is the role of the angle φ in spherical coordinates?
-In spherical coordinates, φ is the angle from the positive z-axis to the projection of the point P onto the xy-plane, effectively determining the azimuthal position of the point.
How does the script illustrate the concept of spherical coordinates?
-The script illustrates the concept of spherical coordinates by describing it as an ordered triple (ρ, θ, φ), where ρ is the distance from the origin, θ is the angle from the z-axis to the projection in the xy-plane, and φ is the angle from the z-axis to the line segment OP.
What is the formula for converting spherical to rectangular coordinates?
-The formulas for converting spherical coordinates (ρ, θ, φ) to rectangular coordinates (X, Y, Z) are X = ρ * sin(φ) * cos(θ), Y = ρ * sin(φ) * sin(θ), and Z = ρ * cos(φ).
Can you provide an example of a conversion from spherical to rectangular coordinates as discussed in the script?
-An example given in the script is converting the spherical coordinates (ρ, θ, φ) = (8, π/4, π) to rectangular coordinates, resulting in (0, 0, -8).
Outlines
📚 Introduction to Cylindrical Coordinates
The script begins with an introduction to cylindrical coordinates, which are an extension of polar coordinates. The concept is explained by adding a z-coordinate to the polar (r, θ) system, resulting in a triple (r, θ, z). The instructor emphasizes the importance of memorizing the formula RθZ for cylindrical coordinates, as it is not provided on the formula sheet. The explanation includes the projection of a point P in the XY plane and the significance of the z-coordinate as the directed distance from the theta plane to point P. The instructor also hints at the ease of drawing cylinders with cylindrical coordinates, which is why they are named as such.
🔢 Conversion Formulas and Examples for Cylindrical to Rectangular Coordinates
The second paragraph delves into the conversion formulas between cylindrical and rectangular coordinates. The formulas are reiterated for clarity, and an example is provided to demonstrate the conversion process from cylindrical (R, θ, Z) to rectangular (X, Y, Z) coordinates. The example involves calculating the exact values of X and Y using trigonometric functions and emphasizes the importance of understanding the quadrant in which the point lies to determine the correct signs for the coordinates. The instructor also discusses the potential for confusion between the formulas and the importance of practice to avoid such errors.
📉 Exploring Rectangular to Cylindrical Conversion with Examples
This section focuses on converting rectangular coordinates to cylindrical coordinates. The instructor outlines the process by starting with the calculation of R squared from the given X and Y values. The example given walks through the steps of finding R, θ, and Z from the rectangular coordinates, emphasizing the correct identification of the quadrant to determine the angle θ. The tangent of θ is calculated, and the angle is identified as π/3. The process is straightforward, and the instructor assures students that practice will make the conversion more manageable.
🎨 Visualizing Cylindrical Coordinates with Graphs
The script introduces the concept of graphing in cylindrical coordinates, providing an example of a circle translated into a 3D space to form a cylinder. The instructor attempts to draw a cylinder to visually explain the concept and mentions that while students are not expected to graph in cylindrical coordinates, understanding the visualization can be beneficial. The mention of x squared plus y squared equaling a constant to form a cylinder is highlighted as a key concept in cylindrical coordinate graphing.
🌐 Transitioning to Spherical Coordinates: An Overview
The instructor transitions the discussion to spherical coordinates, which are more complex due to the presence of two angles. The Greek letter rho (ρ) is introduced as the symbol for the radial distance from the origin, and the angles theta (θ) and phi (φ) are explained as the angles from the positive z-axis and the projection onto the XY plane, respectively. The instructor acknowledges the complexity of spherical coordinates and provides a brief overview before diving into the specifics.
📚 Detailed Explanation of Spherical Coordinate Components
This paragraph provides a detailed explanation of the components of spherical coordinates. The instructor clarifies the roles of rho (ρ), theta (θ), and phi (φ), emphasizing that rho is always positive or zero, and theta and phi are non-negative. The angles are described in relation to the z-axis and the XY plane projection. The instructor also discusses the potential for confusion with the symbol used for phi and its various uses in mathematics.
🧑🏫 Step-by-Step Conversion from Rectangular to Spherical Coordinates
The instructor guides the students through the process of converting rectangular coordinates to spherical coordinates using a specific example. The formulas for the conversion are not provided initially, but the example demonstrates the calculations step by step. The instructor calculates rho squared from the rectangular coordinates, finds theta using the tangent function, and determines phi using the arc cosine function. The final spherical coordinates are presented in the form of rho, theta, phi.
🔄 Conversion from Spherical to Rectangular Coordinates
The final paragraph covers the conversion from spherical to rectangular coordinates. Given a set of spherical coordinates, the instructor demonstrates how to find the corresponding rectangular coordinates using the appropriate formulas. The example provided involves calculating the X, Y, and Z values from the given rho, theta, and phi. The instructor emphasizes the importance of understanding the trigonometric functions involved in the conversion and the significance of the angles in determining the correct coordinates.
Mindmap
Keywords
💡Polar Coordinates
💡Cylindrical Coordinates
💡Theta (θ)
💡Z Coordinate
💡Projection
💡Spherical Coordinates
💡Rho (ρ)
💡Phi (φ)
💡Conversion Formulas
💡Directed Distance
Highlights
Introduction to cylindrical coordinates as an extension of polar coordinates with an additional z-coordinate.
Cylindrical coordinates are represented as R, θ, Z, where R is the radial distance, θ is the angle, and Z is the height.
The conversion formulas from cylindrical to rectangular coordinates and vice versa are discussed.
The concept of projection of a point P in the XY plane using polar coordinates is explained.
Illustration of how adding a Z component to polar coordinates results in cylindrical coordinates, facilitating the drawing of cylinders.
The importance of memorizing the cylindrical to rectangular conversion formulas for problem-solving is emphasized.
A step-by-step example of converting a cylindrical coordinate to rectangular is provided.
Explanation of the trigonometric functions involved in converting between coordinate systems.
The process of converting rectangular coordinates to cylindrical, including the calculation of R, θ, and Z.
Introduction to spherical coordinates as a more complex system involving two angles, Rho, Theta, and Phi.
Spherical coordinates are described as an ordered triple involving Rho for distance, Theta for the angle in the XY plane, and Phi for the angle from the positive Z-axis.
The conversion formulas from spherical to rectangular coordinates are outlined, highlighting the complexity of the process.
A practical example of converting a point from rectangular to spherical coordinates is demonstrated, showcasing the application of the formulas.
The significance of understanding the quadrant in which a point lies when converting coordinates is discussed.
The unique representation of spherical coordinates as they relate to the geometry of a sphere is explained.
A summary of the key formulas and concepts in both cylindrical and spherical coordinate systems for easy reference.
The potential for using spherical coordinates in advanced mathematical and physical applications is mentioned.
The conclusion emphasizes the importance of knowing that these coordinate systems exist for future mathematical studies.
Transcripts
Browse More Related Video
Video 05 - Curvilinear Coordinates
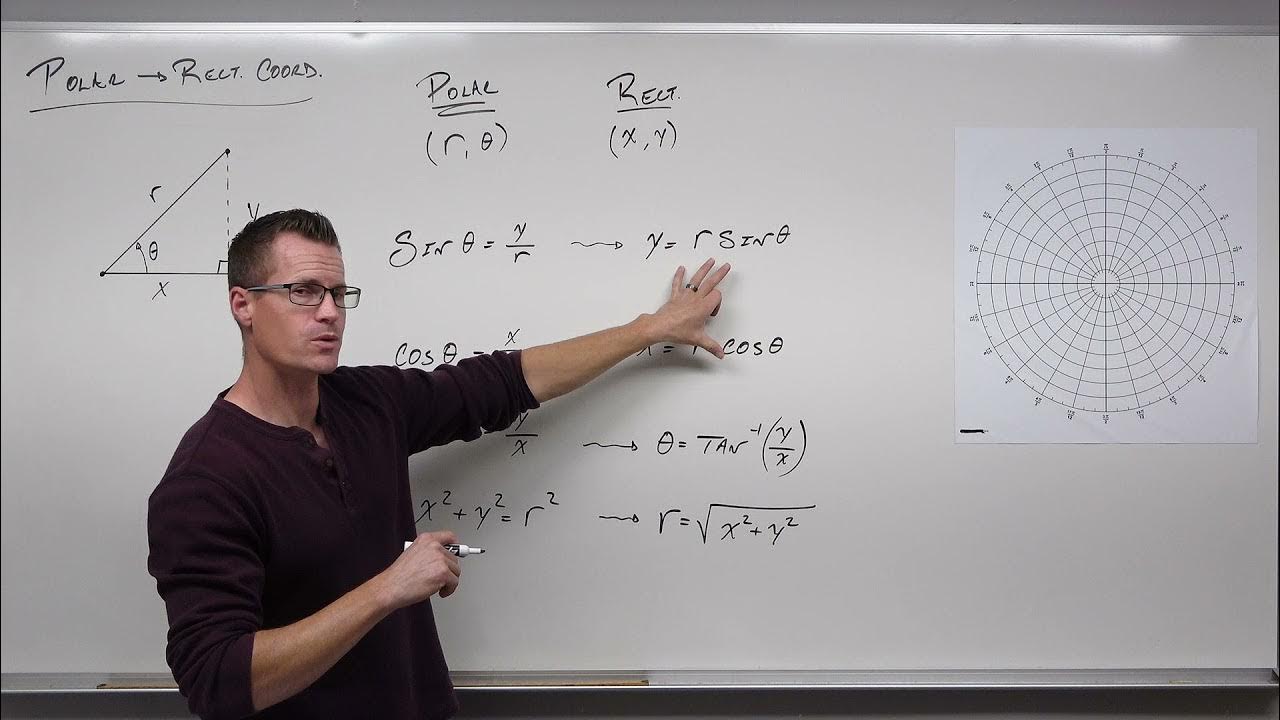
How to Convert From Polar Coordinates to Rectangular Coordinates (Precalculus - Trigonometry 37)

Calculus 3: Triple Integrals in Spherical Coordinates (Video #25) | Math with Professor V
Lec 26: Spherical coordinates; surface area | MIT 18.02 Multivariable Calculus, Fall 2007
Polar Coordinates and Graphing Polar Equations

Video 12 - Jacobian Examples
5.0 / 5 (0 votes)
Thanks for rating: