Lec 26: Spherical coordinates; surface area | MIT 18.02 Multivariable Calculus, Fall 2007

MIT OpenCourseWare

27 Jan 200951:05

EducationalLearning

32 Likes 10 Comments

TLDRThis video script from an MIT OpenCourseWare lecture delves into the concept of spherical coordinates, a system for representing points in space using distance from the origin and two angles. It compares spherical to polar coordinates, explains the transformation between spherical and other coordinate systems, and highlights the utility of spherical coordinates in scenarios with symmetry, especially around the z-axis. The lecture also covers the volume element in spherical coordinates and applies the concept to physical problems, such as calculating gravitational attraction, demonstrating how spherical coordinates simplify the computation.

Takeaways

📚 The lecture introduces spherical coordinates as a method to represent points in space using the distance to the origin and two angles, similar to polar coordinates but extended to three dimensions.
📐 Spherical coordinates are defined by ρ (rho), the distance from the origin, φ (phi), the angle from the positive z-axis, and θ (theta), the angle from the positive x-axis in the xy-plane.
🔄 The transition from Cartesian (x, y, z) to spherical coordinates is facilitated by the relationships z = ρ * cos(φ), r = ρ * sin(φ), x = r * cos(θ), and y = r * sin(θ).
🌐 Spherical coordinates are particularly useful for problems with symmetry, especially those involving the z-axis, making calculations simpler and more intuitive.
📈 The volume element in spherical coordinates, dV, is given by ρ^2 * sin(φ) * dρ * dφ * dθ, which is crucial for setting up triple integrals in this coordinate system.
📘 The script discusses the application of spherical coordinates in calculating volumes of solids, moments of inertia, and gravitational attraction, highlighting their utility in physics and engineering.
🌍 An example provided in the script involves calculating the volume of a spherical cap using spherical coordinates, demonstrating how to set up and evaluate the triple integral with the given bounds.
📊 The calculation of gravitational force using spherical coordinates simplifies when the z-axis is an axis of symmetry, allowing for the integration of the z-component of force due to symmetry.
🧲 Newton's theorem is mentioned, stating that the gravitational attraction of a spherical planet with uniform density is equivalent to that of a point mass at its center, a concept proven using spherical coordinates.
🤔 The script encourages students to think about the concepts in different ways, such as relating spherical coordinates to geographical latitude and longitude, to aid in understanding.
❓ The lecture ends with an invitation for questions, emphasizing the importance of understanding the setup and evaluation process of integrals in spherical coordinates.

Q & A

What are spherical coordinates and how do they differ from cylindrical coordinates?
-Spherical coordinates represent a point in space using the distance to the origin and two angles. They are similar to polar coordinates but extended into three dimensions. They differ from cylindrical coordinates in that spherical coordinates use an angle (phi) from the positive z-axis and another angle (theta) from the x-axis, while cylindrical coordinates use a radial distance and an angle from the x-axis in the xy-plane, with the z-coordinate remaining as in Cartesian coordinates.
What is the Greek letter used to denote the distance from the origin in spherical coordinates?
-The Greek letter used to denote the distance from the origin in spherical coordinates is 'rho' (ρ), which looks like a curly 'p'.
What is the range of values for the angle phi in spherical coordinates?
-The angle phi in spherical coordinates ranges from 0 to π radians (or 0 to 180 degrees), where 0 is on the positive z-axis, π/2 is in the xy-plane, and π is on the negative z-axis.
How is the angle theta in spherical coordinates defined and what is its range?
-Theta in spherical coordinates is defined as the angle counterclockwise from the x-axis after projecting onto the xy-plane. Its range is from 0 to 2π radians, allowing for a full rotation around the z-axis.
What is the relationship between spherical coordinates and the equations of a sphere and a cone?
-In spherical coordinates, setting rho equal to a constant 'a' describes a sphere with radius 'a' centered at the origin. Setting phi equal to a constant value describes a cone with its vertex at the origin and axis along the z-axis. The angle phi determines the opening angle of the cone.
How do you convert between spherical and cylindrical coordinates?
-To convert between spherical and cylindrical coordinates, use the relationships z = rho * cos(phi) and r = rho * sin(phi), where 'r' is the radial distance in cylindrical coordinates, 'rho' is the radial distance in spherical coordinates, and 'phi' is the angle from the z-axis in spherical coordinates.
What is the volume element in spherical coordinates?
-The volume element in spherical coordinates is given by rho squared sine(phi) d rho d phi d theta, which represents a small volume element in a three-dimensional space when integrating over a solid.
How can spherical coordinates be used to find the volume of a spherical cap?
-To find the volume of a spherical cap using spherical coordinates, set up a triple integral with the appropriate bounds for rho, phi, and theta based on the cap's geometry. The volume element is rho squared sine(phi) d rho d phi d theta, and the integral will give the volume of the cap.
What is the physical significance of integrating the product of z and rho squared sine(phi) over a solid in spherical coordinates?
-Integrating the product of z and rho squared sine(phi) over a solid in spherical coordinates can be used to calculate the z-component of the gravitational force exerted by the solid on a test mass at the origin, assuming the solid has a uniform density.
Can you provide an example of how to set up the bounds for a triple integral in spherical coordinates to find the volume of a region?
-An example of setting up bounds for a triple integral in spherical coordinates is given in the script for finding the volume of a portion of a unit sphere above a horizontal plane z = 1/√2. The bounds are rho from 1/√2 / cos(phi) to 1, phi from 0 to π/4, and theta from 0 to 2π.
What is Newton's theorem in the context of gravitational attraction as mentioned in the script?
-Newton's theorem states that the gravitational attraction of a spherical planet with uniform density, or a density that depends only on the distance from the center, is equal to that of a point mass with the same total mass located at the center of the sphere.

Outlines

00:00

📚 Introduction to Spherical Coordinates

The script begins with an introduction to spherical coordinates, emphasizing their importance in advanced mathematical and physics problems. It explains the concept of spherical coordinates by comparing them to polar coordinates, highlighting that spherical coordinates use the distance from the origin and two angles to represent a point in space. The angles, phi and theta, are described in relation to the z-axis and the x-axis, respectively. The explanation includes the range of these angles and how they are used to determine the position of a point in three-dimensional space.

05:05

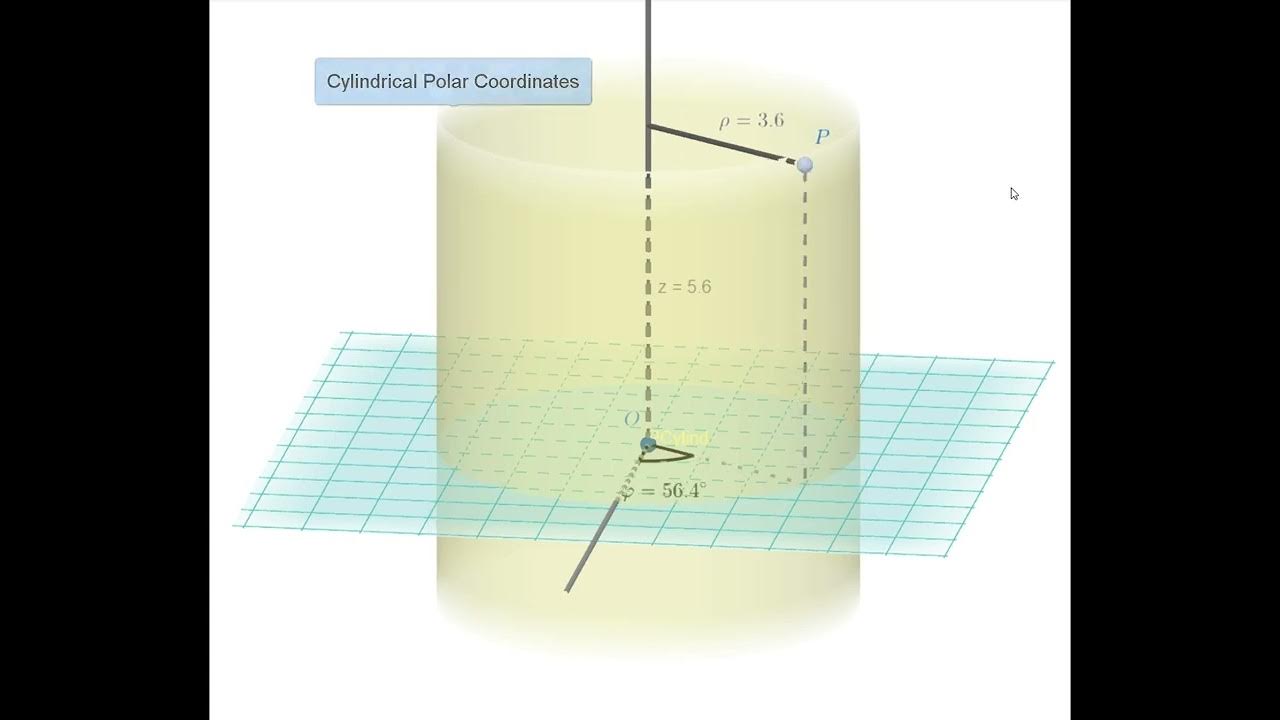
🔍 Transition from Cylindrical to Spherical Coordinates

This paragraph delves into the transition from cylindrical to spherical coordinates, illustrating how to visualize and understand the transformation between these coordinate systems. It discusses the relationship between the radial distance 'r' in cylindrical coordinates and 'rho' in spherical coordinates, as well as the angular relationships. The explanation aids in comprehending how to convert between these systems and the geometric implications of such a conversion.

10:07

📉 Volume Element in Spherical Coordinates

The script introduces the concept of the volume element in spherical coordinates, essential for setting up triple integrals in this coordinate system. It explains how the volume element dV is expressed as rho squared sine phi times d rho, d phi, and d theta. The paragraph provides a geometric interpretation of this volume element by considering the volume of a thin shell between two concentric spheres, leading to the formula for dV in spherical coordinates.

15:11

🌐 Applications of Spherical Coordinates in Physics

This section discusses the applications of spherical coordinates in physics, specifically in the context of gravitational attraction. It outlines the principle that the gravitational force between two masses is proportional to the product of their masses and inversely proportional to the square of the distance between them. The script suggests that placing the solid with symmetry about the z-axis simplifies calculations, as the gravitational force will act along this axis due to symmetry.

20:13

📝 Calculating Gravitational Force Using Spherical Coordinates

The script provides a detailed explanation of how to calculate the gravitational force exerted by a solid object on a test mass using spherical coordinates. It simplifies the calculation by centering the solid on the z-axis, which allows for the gravitational force to be considered only along this axis. The paragraph describes the integral setup for calculating the z-component of the gravitational force and emphasizes the simplification achieved by using spherical coordinates.

25:16

🌌 Newton's Shell Theorem and Spherical Coordinates

The final paragraph discusses Newton's Shell Theorem and its proof using spherical coordinates. The theorem states that the gravitational attraction of a uniformly dense spherical planet is the same as that of a point mass at its center with the same mass. The script outlines the integral setup for this proof and highlights the simplifications that arise when using spherical coordinates, which make the proof more manageable.

Mindmap

Keywords

💡Spherical Coordinates

Spherical coordinates are a three-dimensional coordinate system that represents a point in space by the distance from the origin (denoted by the Greek letter rho, ρ) and two angles (phi, φ, and theta, θ). In the video, this concept is introduced as a method to calculate volumes, areas, and other properties in scenarios where the z-axis plays a special role, such as in problems with symmetry around a central point. The script explains how to transition from Cartesian coordinates (x, y, z) to spherical coordinates and vice versa, using the relationships z = ρcosφ, r = ρsinφ, and expressing x and y in terms of r, θ, and φ.

💡Triple Integrals

Triple integrals are a type of calculus operation used to calculate volumes, mass, average values, and other properties of three-dimensional objects. The script discusses how to perform triple integrals in spherical coordinates, which is particularly useful when dealing with symmetrical shapes or when the z-axis is a natural axis of symmetry. The video script provides an example of setting up a triple integral in spherical coordinates to find the volume of a spherical cap.

💡Volume Element

In the context of the video, the volume element dV in spherical coordinates is given by ρ^2sinφ dρ dφ dθ. It represents the volume of an infinitesimally small portion of a three-dimensional object and is used in integral calculus to find the total volume under a surface or within a solid. The script explains how to derive this volume element and how it simplifies the process of integrating over complex three-dimensional regions.

💡Gravitational Attraction

Gravitational attraction is the force that causes objects with mass to be attracted to one another. In the script, it is discussed in the context of calculating the gravitational force exerted by a solid object on a point mass (test mass) at the origin. The force is proportional to the product of the two masses and inversely proportional to the square of the distance between them, as described by Newton's law of universal gravitation.

💡Density

Density, symbolized by the Greek letter delta (δ) in the script, refers to the mass per unit volume of a substance. It is an important factor in calculating the gravitational force exerted by a solid with a non-uniform mass distribution. The script explains that the mass of a small volume element in an integral can be found by multiplying the density by the volume element dV.

💡Symmetry

Symmetry in the context of the video refers to the property of an object that allows it to be arranged in a way that parts of it are mirror images of other parts. The script emphasizes the importance of symmetry, particularly rotational symmetry around the z-axis, in simplifying calculations involving spherical coordinates and gravitational forces.

💡Cylindrical Coordinates

Cylindrical coordinates are another three-dimensional coordinate system that is useful for describing points in space in terms of a distance from a chosen reference axis (often the z-axis), an angle from a reference direction, and a height along the axis. The script mentions cylindrical coordinates as a stepping stone to understanding spherical coordinates and as an alternative system for setting up integrals.

💡Latitude and Longitude

In the script, the terms latitude and longitude are used as an analogy to help understand spherical coordinates. Latitude (analogous to φ, phi) measures the distance from the 'North Pole' or z-axis, while longitude (analogous to θ, theta) measures the angle around the z-axis from a reference direction, similar to how longitude lines run around the Earth.

💡Polar Coordinates

Polar coordinates are a two-dimensional coordinate system where each point is determined by a radius (distance from a point, usually the origin) and an angle from a reference direction. The script mentions polar coordinates as a simpler version of spherical coordinates, where the 'polar' concept is extended into three dimensions by adding the z-axis.

💡Gravitational Force

Gravitational force is the attractive force that the Earth (or any celestial body) exerts on objects. The script discusses how to calculate the gravitational force on a test mass at the origin due to a solid with a given mass distribution, using the formula involving G (the gravitational constant), the masses of the objects, and the distance between their centers of mass.

Highlights

Introduction to spherical coordinates as a method to represent a point in space using the distance to the origin and two angles.

Comparison of spherical coordinates to polar coordinates, emphasizing their use in three-dimensional space.

Explanation of the Greek letter rho (ρ) representing the distance from the origin in spherical coordinates.

Description of the angles phi (φ) and theta (θ) used in spherical coordinates to determine direction.

Illustration of phi as the angle downwards from the z-axis and its range between 0 and π.

Clarification of theta as the angle counterclockwise from the x-axis in the xy-plane.

Suggestion to think of spherical coordinates in terms of latitude and longitude, with phi as latitude and theta as longitude.

Transition from cylindrical to spherical coordinates by considering the rz plane.

Conversion formulas between spherical and cylindrical coordinates, specifically relating rho, phi, and r.

Derivation of the volume element in spherical coordinates, rho squared sine phi d rho d phi d theta.

Application of spherical coordinates in scenarios with symmetry, especially where the z-axis plays a special role.

Example of setting up triple integrals in spherical coordinates for a geometric problem involving a sphere and a slanted plane.

Explanation of the volume element for surface area on a sphere and its relation to spherical coordinates.

Demonstration of how to find the volume of a spherical cap using spherical coordinates.

Discussion on the application of spherical coordinates in physics, particularly in calculating gravitational attraction.

Introduction to Newton's theorem on the gravitational attraction of a spherical planet with uniform density, equating it to a point mass at its center.

Simplification of gravitational force calculations in spherical coordinates by leveraging symmetry and the z-axis.

Final remarks on the practicality of spherical coordinates in calculating gravitational forces and moments of inertia.

Transcripts

Browse More Related Video

Calculus 3: Triple Integrals in Spherical Coordinates (Video #25) | Math with Professor V

Calculus 3: Lecture 11.7 Cylindrical and Spherical Coordinates

Integration in Spherical Coordinates

Video 05 - Curvilinear Coordinates

Triple Integrals in Spherical Coordinates

Video 40 - Gradient Examples

Related Tags

Spherical Coordinates MIT OCW Calculus Physics Gravitational Force Mathematics Educational Resources Vector Calculus Volume Integration Polar to Spherical