Video 12 - Jacobian Examples
TLDRThis video delves into tensor calculus, focusing on the Jacobian matrix across various coordinate systems. It begins with affine coordinates, explaining the Jacobian and its inverse, followed by covariant transformations to derive basis vectors in Cartesian coordinates. The script then covers plane polar, cylindrical polar, and spherical polar coordinates, detailing the Jacobian for transformations and the process of obtaining basis vectors. The video aims to clarify the concepts with practical examples, emphasizing the constancy of the Jacobian in affine coordinates and the complexity in curvilinear systems.
Takeaways
- 📚 The video is part of a series on tensor calculus, focusing on the Jacobian matrix in various coordinate systems.
- 🔍 The script explains the Jacobian in the context of affine coordinates, detailing its components and representation as a matrix.
- 🧠 The process of finding the Jacobian involves taking partial derivatives of transformed coordinates with respect to the original coordinates.
- 📏 For affine coordinates, the partial derivatives are constants, indicating the Jacobian and its inverse are the same throughout the entire space.
- 🔄 The script demonstrates how to find the inverse Jacobian, which involves taking derivatives of the unprimed coordinates with respect to the primed coordinates.
- 🌐 The video covers covariant transformations, showing how to derive covariant basis vectors in terms of Cartesian coordinates.
- 📈 The script provides explicit formulas for the basis vectors in the affine coordinate system and emphasizes their constancy across the space.
- 📊 The video moves on to plane polar coordinates, explaining the Jacobian and its inverse, and how to derive the covariant basis vectors.
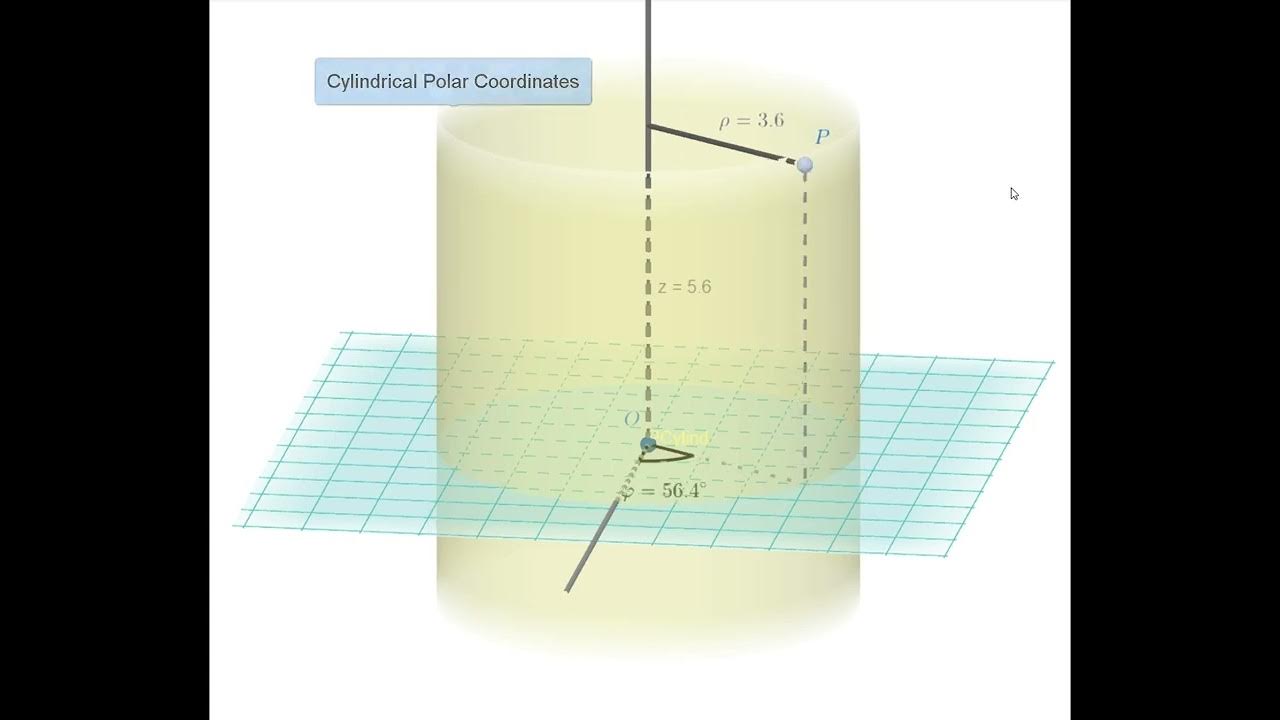
- 📐 Cylindrical polar coordinates are discussed, showing the similarity to plane polar coordinates but with an additional Z dimension.
- 🌍 Spherical polar coordinates are the final topic, with the script detailing the Jacobian, its inverse, and the basis vectors for this three-dimensional system.
- 🎯 The script concludes by emphasizing the importance of understanding the Jacobian and covariant transformations for working with different coordinate systems in tensor calculus.
Q & A
What is the main topic of this video?
-The main topic of this video is tensor calculus, specifically focusing on the Jacobian matrix and its applications in various coordinate systems.
What is the Jacobian matrix?
-The Jacobian matrix is a matrix representation of all first-order partial derivatives of a vector-valued function. It describes how a function transforms small displacements in the input space to small displacements in the output space.
In the context of this video, how is the Jacobian matrix represented?
-In this video, the Jacobian matrix is represented as a 2x2 matrix for two-dimensional transformations, with entries representing the partial derivatives of the transformed coordinates with respect to the original coordinates.
What are affine coordinates?
-Affine coordinates are a type of coordinate system where the transformation between the original and transformed coordinates is linear. The Jacobian for affine coordinates is constant throughout the entire space.
How does the video demonstrate finding the Jacobian for affine coordinates?
-The video demonstrates finding the Jacobian for affine coordinates by taking the partial derivatives of the transformed coordinates with respect to the original coordinates and organizing them into a matrix form.
What is the inverse Jacobian matrix?
-The inverse Jacobian matrix is the matrix that, when multiplied by the Jacobian matrix, yields the identity matrix. It represents the transformation from the transformed coordinates back to the original coordinates.
How does the video explain the covariant transformation?
-The video explains the covariant transformation by using the Jacobian matrix with the free index at the bottom, showing how to derive the covariant basis vectors in terms of Cartesian coordinates.
What are plane polar coordinates?
-Plane polar coordinates are a two-dimensional coordinate system where points are defined by the distance from the origin (r) and the angle from the positive x-axis (theta).
How does the video calculate the Jacobian for plane polar coordinates?
-The video calculates the Jacobian for plane polar coordinates by taking the partial derivatives of x and y with respect to r and theta, and organizing these derivatives into a matrix.
What are cylindrical polar coordinates?
-Cylindrical polar coordinates are a three-dimensional coordinate system where points are defined by the radial distance from the z-axis (rho), the angle from the positive x-axis in the xy-plane (phi), and the height above the xy-plane (z).
How does the video find the basis vectors for cylindrical polar coordinates?
-The video finds the basis vectors for cylindrical polar coordinates by multiplying each item in the Jacobian matrix by the corresponding unit vectors in Cartesian coordinates (x-hat, y-hat, and z-hat).
What are spherical polar coordinates?
-Spherical polar coordinates are a three-dimensional coordinate system where points are defined by the radial distance from the origin (r), the polar angle measured from the positive z-axis (theta), and the azimuthal angle in the xy-plane from the positive x-axis (phi).
How does the video demonstrate the Jacobian for spherical polar coordinates?
-The video demonstrates the Jacobian for spherical polar coordinates by taking the partial derivatives of x, y, and z with respect to r, theta, and phi, and presenting these in a matrix form.
What is the significance of the Jacobian being constant in affine coordinates?
-The significance of the Jacobian being constant in affine coordinates is that it implies the transformation is linear and the basis vectors and the inverse Jacobian are the same throughout the entire space, which is not generally true for curvilinear coordinates.
Outlines
📚 Introduction to Jacobian Matrices in Tensor Calculus
This paragraph introduces the concept of the Jacobian matrix within the context of tensor calculus. The video script begins with an overview of the Jacobian, explaining its role in transforming between different coordinate systems. It uses affine coordinates as an example, illustrating how the Jacobian can be represented as a matrix with entries that correspond to partial derivatives. The script then demonstrates how to calculate the Jacobian for affine coordinates, showing the process of taking partial derivatives with respect to different variables and organizing them into a matrix format. The inverse Jacobian is also discussed, highlighting its importance in transforming coordinates back to their original system.
🔍 Deriving Covariant Basis Vectors and Affine Coordinates
The second paragraph delves into the process of deriving covariant basis vectors and expressing affine coordinates in terms of Cartesian coordinates. It explains the covariant transformation, which involves the use of the Jacobian with a free index at the bottom, and how this transformation can be expanded to include summation over dummy indices. The script provides explicit formulas for deriving the basis vectors in the affine coordinate system and demonstrates how to apply these formulas to obtain the basis vectors as functions of Cartesian coordinates. The significance of the Jacobian, inverse Jacobian, and basis vectors being constant throughout the entire space in affine coordinates is also highlighted, contrasting this feature with curvilinear coordinates.
📈 Jacobian Calculations for Plane Polar and Cylindrical Polar Coordinates
This paragraph focuses on calculating the Jacobian for plane polar and cylindrical polar coordinates. It begins with the Jacobian for plane polar coordinates, detailing the partial derivatives of x and y with respect to r and theta, and then moves on to the inverse Jacobian. The process involves taking partial derivatives of the radial and angular coordinates with respect to Cartesian coordinates and vice versa. The script then transitions to cylindrical polar coordinates, which introduces a third dimension. The Jacobian for cylindrical coordinates is shown to be an extension of the plane polar case, with additional terms for the z-component, which does not depend on the radial or angular coordinates.
🌐 Exploring Spherical Polar Coordinates and Their Jacobian
The fourth paragraph discusses the Jacobian for spherical polar coordinates, which adds another layer of complexity due to the three-dimensional nature of the coordinate system. The script outlines the partial derivatives of x, y, and z with respect to the spherical coordinates r, theta, and phi. It then provides a brief overview of how to find the inverse Jacobian, although it acknowledges the tedious nature of the calculations and opts to present the results directly. The basis vectors in spherical polar coordinates are also derived, showing how each column of the Jacobian matrix can be multiplied by the respective Cartesian basis vectors to obtain the spherical basis vectors.
🎓 Summary of Jacobian and Covariant Transformation Understanding
The final paragraph serves as a summary, aiming to reinforce the viewer's understanding and appreciation of the Jacobian and covariant transformations. It encapsulates the essence of the video series on tensor calculus, emphasizing the importance of the Jacobian in coordinate transformations and the process of deriving covariant basis vectors. The paragraph concludes with an encouragement for viewers to practice these concepts to solidify their grasp of tensor calculus.
Mindmap
Keywords
💡Tensor Calculus
💡Jacobian
💡Affine Coordinates
💡Partial Derivative
💡Covariant Transformation
💡Basis Vectors
💡Polar Coordinates
💡Cylindrical Polar Coordinates
💡Spherical Polar Coordinates
💡Inverse Jacobian
Highlights
Introduction to the concept of the Jacobian matrix in tensor calculus with examples.
Explanation of the Jacobian matrix as a representation of the transformation between coordinate systems.
Description of the Jacobian matrix for affine coordinates, emphasizing its constant nature throughout the entire space.
Calculation of the Jacobian for affine coordinates using partial derivatives with respect to different variables.
Derivation of the inverse Jacobian matrix for affine coordinates, showcasing the relationship between primed and unprimed coordinates.
Application of covariant transformation to derive covariant basis vectors in terms of Cartesian coordinates.
Demonstration of how the Jacobian matrix remains constant in affine coordinates, unlike in curvilinear coordinates.
Transition to plane polar coordinates, outlining the process for calculating the Jacobian matrix.
Calculation of the inverse Jacobian for plane polar coordinates, highlighting the complexity of the process.
Derivation of covariant basis vectors for plane polar coordinates using the Jacobian matrix.
Introduction to cylindrical polar coordinates, emphasizing the extension to three dimensions.
Calculation of the Jacobian matrix for cylindrical polar coordinates, showing its similarity to plane polar coordinates.
Derivation of the basis vectors for cylindrical polar coordinates, illustrating the impact of the additional Z dimension.
Transition to spherical polar coordinates, discussing the complexities of the Jacobian matrix in this system.
Calculation of the Jacobian matrix for spherical polar coordinates, detailing the partial derivatives with respect to R, Theta, and Phi.
Derivation of the inverse Jacobian matrix for spherical polar coordinates, acknowledging the tedious nature of the process.
Final derivation of the basis vectors for spherical polar coordinates, completing the comprehensive overview of the topic.
Conclusion summarizing the importance of the Jacobian and covariant transformations in understanding coordinate systems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: