Intermediate value theorem to prove a root in an interval (KristaKingMath)

Krista King

10 Sept 201204:54

EducationalLearning

32 Likes 10 Comments

TLDRIn this informative video, the presenter explains the application of the Intermediate Value Theorem to demonstrate the existence of a root for a function within a given interval. By evaluating the function at the endpoints of the interval [1, 2] for f(x) = x^4 + x - 3, the presenter shows that the function values change from negative to positive, indicating a root must exist between these points. The explanation clarifies how the theorem ensures that the function assumes every value between the function values at the interval endpoints, thus confirming the presence of a root without directly solving the equation.

Takeaways

📚 The video discusses the application of the Intermediate Value Theorem to prove the existence of a root for a function within a given interval.
📈 The function in question is f(x) = x^4 + x - 3, and the interval of interest is from 1 to 2.
🔍 To apply the theorem, the function is evaluated at the endpoints of the interval: f(1) and f(2).
📉 The value of f(1) is calculated to be -1, indicating the function has a negative value at the lower endpoint of the interval.
📈 The value of f(2) is found to be 15, showing the function has a positive value at the upper endpoint of the interval.
🤔 The assumption is made that since the function values at the endpoints have opposite signs, there must be a root between them.
📝 The Intermediate Value Theorem is then explained, stating that a continuous function will take on every value between its values at two points.
📌 The theorem guarantees that there is at least one point c in the interval (1, 2) where f(c) = 0, confirming the existence of a root.
📊 The video emphasizes the importance of proving the existence of a root rather than just assuming it based on the sign change.
📚 The process of applying the theorem is demonstrated step by step, from evaluating the function at the interval endpoints to concluding the existence of a root.
👍 The video concludes by encouraging viewers to like and subscribe for more educational content.

Q & A

What is the main topic of the video?
-The main topic of the video is the application of the Intermediate Value Theorem to prove the existence of a root for a given function within a specific interval.
What is the function in the problem discussed in the video?
-The function discussed in the video is f(x) = x^4 + x - 3.
What interval is the video focusing on to find a root of the function?
-The video focuses on finding a root of the function within the interval [1, 2].
What is the value of the function at x = 1?
-The value of the function at x = 1 is f(1) = 1^4 + 1 - 3, which simplifies to -1.
What is the value of the function at x = 2?
-The value of the function at x = 2 is f(2) = 2^4 + 2 - 3, which simplifies to 15.
What does the Intermediate Value Theorem state?
-The Intermediate Value Theorem states that if a function is continuous on a closed interval [a, b] and takes on different values at a and b, then it must take on every value between those two values at least once within the interval.
How does the video demonstrate that the function has a root between x = 1 and x = 2?
-The video demonstrates this by showing that the function has a negative value at x = 1 and a positive value at x = 2, and then applying the Intermediate Value Theorem to conclude that there must be a root between these two points.
What is the significance of the function's values at the endpoints of the interval?
-The significance of the function's values at the endpoints is that they establish the necessary condition for the Intermediate Value Theorem to be applied, which is having different signs at the endpoints.
What is the root of a function?
-The root of a function is the value of the variable for which the function equals zero, indicating where the graph of the function crosses the x-axis.
How does the video explain the concept of the function assuming every value between f(a) and f(b)?
-The video explains this by using a visual analogy of a graph, stating that if the function has values f(a) and f(b) at points a and b on the x-axis, it must pass through every y-value between f(a) and f(b), including zero if f(a) and f(b) have opposite signs.
What does the inequality f(1) < 0 and 0 < f(2) imply about the function?
-The inequality implies that the function changes sign between x = 1 and x = 2, which, according to the Intermediate Value Theorem, guarantees the existence of at least one root in that interval.

Outlines

00:00

📈 Introduction to the Intermediate Value Theorem

In this segment, we introduce the Intermediate Value Theorem and outline its purpose: to prove that a function has a root within a given interval. We will demonstrate this by evaluating the function at both ends of the interval and showing that the graph of the function crosses the x-axis between these values.

📊 Example Problem Setup

We describe a specific problem where we use the Intermediate Value Theorem to show that the function f(x) = x⁴ + x - 3 has a root in the interval [1, 2]. The root of a function is defined as the point where the graph crosses the x-axis.

🔢 Evaluating Function at Interval Ends

We evaluate the function at the endpoints of the interval. Plugging in x=1, we find f(1) = -1. Plugging in x=2, we find f(2) = 15. These calculations are essential for applying the Intermediate Value Theorem.

📐 Intermediate Value Theorem Application

We discuss the assumptions we can make based on the calculated values at the interval's ends. With f(1) negative and f(2) positive, we assume that the function must cross the x-axis at some point between 1 and 2, indicating the presence of a root.

🧮 Detailed Explanation of the Theorem

The Intermediate Value Theorem states that if a function is continuous on a closed interval [a, b], and takes on different signs at the endpoints, then it must take on every value between f(a) and f(b) within that interval. We illustrate this concept with a hypothetical graph.

⚖️ Applying the Theorem to Our Problem

By applying the theorem to our specific problem, we note that the function values at the endpoints of the interval are -1 and 15. According to the theorem, since the function is continuous and spans negative to positive values, there must be a root (f(c) = 0) between 1 and 2.

🔍 Conclusion and Summary

We summarize how we used the Intermediate Value Theorem to determine that the function has a root in the interval [1, 2]. We conclude with a reminder of the importance of the theorem in proving the existence of roots within an interval.

👍 Final Remarks and Call to Action

We wrap up the video by encouraging viewers to like the video and subscribe for notifications about future content, hoping they found the explanation helpful.

Mindmap

Keywords

💡Intermediate Value Theorem

The Intermediate Value Theorem is a fundamental concept in calculus that states if a continuous function takes on different values at two points, then it must also take on every value in between at some point within that interval. In the video, this theorem is used to prove that the function f(x) = x^4 + x - 3 has a root between the interval [1, 2]. The theorem is central to the video's theme of demonstrating the existence of a root without explicitly finding it.

💡Root

A root of a function is a value of x for which the function equals zero. In the context of the video, the root is the point where the graph of the function f(x) crosses the x-axis. The script discusses using the Intermediate Value Theorem to prove that a root exists between 1 and 2 for the given function.

💡Function

A function is a mathematical relationship between two sets that assigns to each element from the first set exactly one element of the second set. In the video, the function in question is f(x) = x^4 + x - 3, and the script explains how to determine if this function has a root within a specific interval.

💡Graph

In mathematics, a graph is a visual representation of a set of points, representing the mapping of a function. The script uses the term 'graph' to describe the visual aspect of the function and how it crosses the x-axis, indicating the presence of a root.

💡Interval

An interval in mathematics is a set of real numbers with a lower and upper bound. The script specifically discusses the interval [1, 2], within which the video aims to prove the existence of a root for the given function.

💡Evaluate

To evaluate a function means to calculate its value at a specific point. The script describes evaluating the function f(x) at the endpoints of the interval, which is a step in applying the Intermediate Value Theorem.

💡Continuous Function

A continuous function is one that does not have any abrupt changes in value, and its graph can be drawn without lifting the pen from the paper. The Intermediate Value Theorem applies to continuous functions, as mentioned in the script when discussing the function f(x).

💡X-axis

The x-axis is the horizontal axis in the Cartesian coordinate system, and it is where the roots of a function are located. The script refers to the x-axis as the point of intersection between the graph of the function and the horizontal axis.

💡Value

In the context of the script, a value refers to the numerical result obtained when the function is evaluated at a specific point. The Intermediate Value Theorem is about the function assuming every value between two points within an interval.

💡Inequality

An inequality is a mathematical statement that compares two expressions that are not necessarily equal, using symbols such as 'less than' or 'greater than'. The script uses the concept of inequality to show that since f(1) is less than zero and f(2) is greater than zero, there must be a root between these two values.

💡Proof

A proof is a series of logical steps that demonstrate the truth of a statement. In the video, the proof involves using the Intermediate Value Theorem to show that there is a root of the function within the interval [1, 2].

Highlights

Introduction to the Intermediate Value Theorem and its application in proving the existence of a root within a given interval.

Explanation of the root of a function as the point where the graph crosses the x-axis.

Demonstration of how to apply the Intermediate Value Theorem to the function f(x) = x^4 + x - 3 on the interval [1, 2].

Evaluation of the function at the interval endpoints, showing f(1) = -1 and f(2) = 15.

Assumption that a negative value at one endpoint and a positive value at the other implies a root exists between them.

Clarification on the need for formal proof using the Intermediate Value Theorem to confirm the existence of a root.

Description of the theorem's principle that a function must assume every value between two points on the x-axis.

Graphical representation of the function's graph and how it meets the criteria of the theorem.

Explanation of the theorem's implication that there must be a point c where f(c) = 0, indicating a root.

Application of the theorem to the given problem, establishing the existence of a root between 1 and 2.

Use of inequalities f(1) < 0 and 0 < f(2) to illustrate the theorem's application and the conclusion of a root's existence.

Emphasis on the importance of the Intermediate Value Theorem in proving the existence of roots without direct calculation.

Instruction on how to indicate the existence of a root using the theorem's criteria.

Encouragement for viewers to like and subscribe for more educational content.

Summary of the video's educational value and its contribution to understanding the Intermediate Value Theorem.

Transcripts

Browse More Related Video

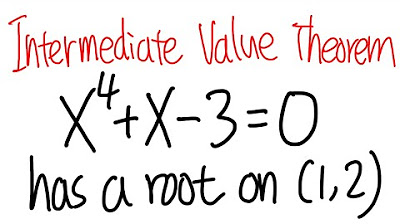
Intermediate Value Theorem, calculus 1 tutorial, showing a root of a function on an interval

Intermediate Value Theorem Explained - To Find Zeros, Roots or C value - Calculus

Intermediate value theorem example | Existence theorems | AP Calculus AB | Khan Academy

Justification with the intermediate value theorem: equation | AP Calculus AB | Khan Academy

Prove the equation has at least one real root (KristaKingMath)

Intermediate Value Theorem: show function has at least one solution -- CALCULUS