Intermediate Value Theorem: show function has at least one solution -- CALCULUS

INeedToPassCalculus
18 Jan 202105:41
EducationalLearning
32 Likes 10 Comments

TLDRIn this video, we explore how to demonstrate that the equation \( x^3 + x - 1 = 0 \) has at least one solution using the Intermediate Value Theorem (IVT). The host explains that for continuous functions, if the function's value changes from negative to positive over an interval, it must cross zero within that interval. By evaluating the function at the endpoints 0 and 1, and finding the values -1 and 1 respectively, the host concludes that a solution exists between 0 and 1. The video invites viewers to comment with any tricky theorem problems they encounter.

Takeaways
  • 🧑‍🏫 The video is a calculus lesson focused on demonstrating the existence of at least one solution to the equation \( x^3 + x - 1 = 0 \).
  • 🔍 The presenter suggests using the Intermediate Value Theorem (IVT) to show the existence of a solution, which is applicable to continuous functions.
  • 📉 The IVT is often used when a function changes from a negative value to a positive value, indicating the presence of a root between the endpoints.
  • 📈 The presenter proposes considering the function \( f(x) = x^3 + x - 1 \) and checking its values at specific endpoints to apply the IVT.
  • 📍 An interval of [0, 1] is suggested for testing the function values, starting with \( f(0) \) and \( f(1) \).
  • 🔢 At \( x = 0 \), the function value is \( -1 \), and at \( x = 1 \), it is \( 1 \), showing a change from negative to positive.
  • 📚 Since the function is continuous and changes from a negative to a positive value within the interval [0, 1], the IVT guarantees a root exists in this interval.
  • 📝 The presenter advises that the justification for the solution should reference the continuity of the polynomial function and the application of the IVT.
  • 📑 The lesson includes a step-by-step explanation of how to apply the IVT to the given problem, emphasizing the change in function values at the interval endpoints.
  • 🤔 The video encourages viewers to think about variations of theorem problems and invites them to ask questions in the comments for further clarification.
  • 📚 The presenter also mentions other theorems like the Mean Value Theorem and Rolle's Theorem, indicating the complexity and variety of calculus theorem questions.
Q & A

  • What is the main topic of the video script?

    -The main topic of the video script is to demonstrate that the equation x cubed plus x minus one equals zero has at least one solution using the Intermediate Value Theorem (IVT).

  • What is the Intermediate Value Theorem (IVT)?

    -The Intermediate Value Theorem (IVT) states that if a function is continuous on a closed interval [a, b] and takes on different values at the endpoints, then it must take on every value between those endpoints at least once.

  • Why does the script suggest using the IVT for this problem?

    -The script suggests using the IVT because the problem requires showing that a certain function has at least one root, and the IVT is a powerful tool for proving the existence of roots for continuous functions.

  • What function is being discussed in the script?

    -The function being discussed in the script is f(x) = x^3 + x - 1.

  • What is the significance of the function values at the endpoints of the interval [0, 1]?

    -The significance of the function values at the endpoints of the interval [0, 1] is that they are used to demonstrate that the function changes sign, which, according to the IVT, implies the existence of a root within the interval.

  • What is the function value when x = 0?

    -When x = 0, the function value is f(0) = 0^3 + 0 - 1, which simplifies to -1.

  • What is the function value when x = 1?

    -When x = 1, the function value is f(1) = 1^3 + 1 - 1, which simplifies to 1.

  • Why does the change in function value from negative to positive between x = 0 and x = 1 indicate the existence of a root?

    -The change from a negative function value at x = 0 to a positive function value at x = 1 indicates that the function must cross the x-axis at some point in between, which is the definition of a root.

  • What is the conclusion of the script regarding the equation x cubed plus x minus one equals zero?

    -The conclusion of the script is that, by applying the IVT to the function f(x) = x^3 + x - 1, it is proven that there exists at least one x value for which the equation equals zero.

  • How can the script be used to help understand the application of the IVT in calculus?

    -The script provides a step-by-step example of how to apply the IVT to a specific function to prove the existence of a root, which can help students understand the practical application of the theorem in solving calculus problems.

  • What does the script suggest for those who have questions about theorems or the problem discussed?

    -The script suggests that viewers who have questions about the theorems or the problem discussed should leave a comment, and the presenter looks forward to answering those questions.

Outlines
00:00
📚 Demonstrating the Existence of a Solution Using the Intermediate Value Theorem

This paragraph introduces a calculus problem that requires showing the equation x³ + x - 1 = 0 has at least one solution. The speaker suggests using the Intermediate Value Theorem (IVT), which applies to continuous functions and states that if a function changes from a negative to a positive value over an interval, it must cross zero at some point within that interval. The example provided involves evaluating the function f(x) = x³ + x - 1 at x = 0 and x = 1, which yields values of -1 and 1, respectively. The IVT is then applied to assert that since the function is continuous and changes sign, there must be a root between 0 and 1. The speaker emphasizes that the IVT can be applied because polynomials, like the one in question, are continuous over all real numbers.

05:02
🤔 Addressing Variations and Challenges in Theorem-Based Problems

The second paragraph discusses the potential complexity and variations in theorem-based problems in calculus, such as those involving the Mean Value Theorem, Rolle's Theorem, or the Intermediate Value Theorem. The speaker invites viewers to share in the comments if they encounter particularly tricky theorem problems or if there are aspects of the current explanation that are unclear. The speaker expresses eagerness to engage with the audience's questions and concludes with well-wishes for the day.

Mindmap
Keywords
💡Intermediate Value Theorem (IVT)
The Intermediate Value Theorem (IVT) states that for any continuous function f(x) on a closed interval [a, b], if f(a) and f(b) have opposite signs, there exists at least one c in (a, b) such that f(c) = 0. In the video, this theorem is used to show that the equation x^3 + x - 1 = 0 has at least one solution by evaluating the function at the endpoints of the interval [0, 1].
💡Continuous Function
A continuous function is a type of function where small changes in the input result in small changes in the output, without any abrupt jumps or breaks. In the video, the speaker mentions that the function f(x) = x^3 + x - 1 is continuous, which is a key requirement for applying the Intermediate Value Theorem.
💡Polynomial
A polynomial is a mathematical expression involving a sum of powers in one or more variables multiplied by coefficients. The video focuses on the polynomial f(x) = x^3 + x - 1, discussing its properties and behavior within a certain interval to demonstrate the existence of a root.
💡X-Intercept
An x-intercept is the point where a graph of a function crosses the x-axis, meaning the function's value is zero at that point. In the video, the goal is to show that the polynomial x^3 + x - 1 has an x-intercept, which corresponds to finding a root of the equation.
💡Function Height
Function height refers to the value of the function f(x) at a particular x. In the video, the speaker evaluates the function height at the endpoints of the interval [0, 1] to show that the function changes sign, thereby using the Intermediate Value Theorem to conclude there is a root in that interval.
💡Interval
An interval is a range of values between two endpoints. In the video, the interval [0, 1] is chosen to apply the Intermediate Value Theorem to the function f(x) = x^3 + x - 1, checking the function values at the endpoints to infer the existence of a root.
💡Root
A root of a function is a value of x for which the function f(x) equals zero. The video demonstrates that the polynomial x^3 + x - 1 has at least one root by applying the Intermediate Value Theorem over the interval [0, 1].
💡Negative Height
Negative height refers to a function value that is less than zero. In the video, the function f(x) = x^3 + x - 1 is evaluated at x = 0, resulting in a negative height, which is used as part of the argument to apply the Intermediate Value Theorem.
💡Positive Height
Positive height refers to a function value that is greater than zero. In the video, the function f(x) = x^3 + x - 1 is evaluated at x = 1, resulting in a positive height, which, along with the negative height at x = 0, supports the application of the Intermediate Value Theorem.
💡Justification
Justification in the context of the video refers to the reasoning provided to support the claim that the function has at least one root. The speaker justifies the use of the Intermediate Value Theorem by showing that the function is continuous and that its values at the endpoints of the interval [0, 1] have opposite signs.
Highlights

The problem is to show that the equation x^3 + x - 1 = 0 has at least one solution.

The intermediate value theorem (IVT) is suggested as a method to prove the existence of at least one solution.

IVT is applicable to continuous functions and shows that if a function changes from a negative to a positive value, it must pass through zero at some point in between.

The function f(x) = x^3 + x - 1 is a polynomial, hence continuous everywhere, allowing the use of IVT.

To apply IVT, choose an interval and evaluate the function at the endpoints.

The interval [0, 1] is chosen for the example, with f(0) = -1 and f(1) = 1.

Since f(0) < 0 and f(1) > 0, by IVT, there must be a root in the interval [0, 1].

The existence of a root is justified by the continuity of the function and the change in sign of the function values.

The solution process demonstrates the application of IVT to a polynomial equation.

The video provides a clear example of how to use IVT to find a root of a function.

The presenter suggests that there are many variations of theorem application problems and encourages viewers to ask questions if they encounter challenging ones.

The video aims to clarify the use of IVT and other theorems in solving calculus problems.

The presenter invites viewers to comment with any particularly tricky theorem problems they are facing.

The video concludes by encouraging viewers to engage with the content and ask questions.

The presenter looks forward to addressing the questions and problems posed by the viewers.

The video ends with a positive note, wishing viewers a wonderful day.

Transcripts

Browse More Related Video

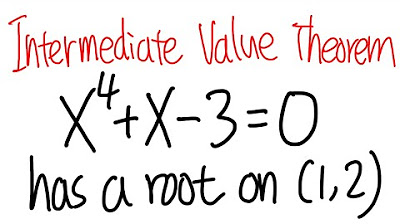
Intermediate Value Theorem, calculus 1 tutorial, showing a root of a function on an interval

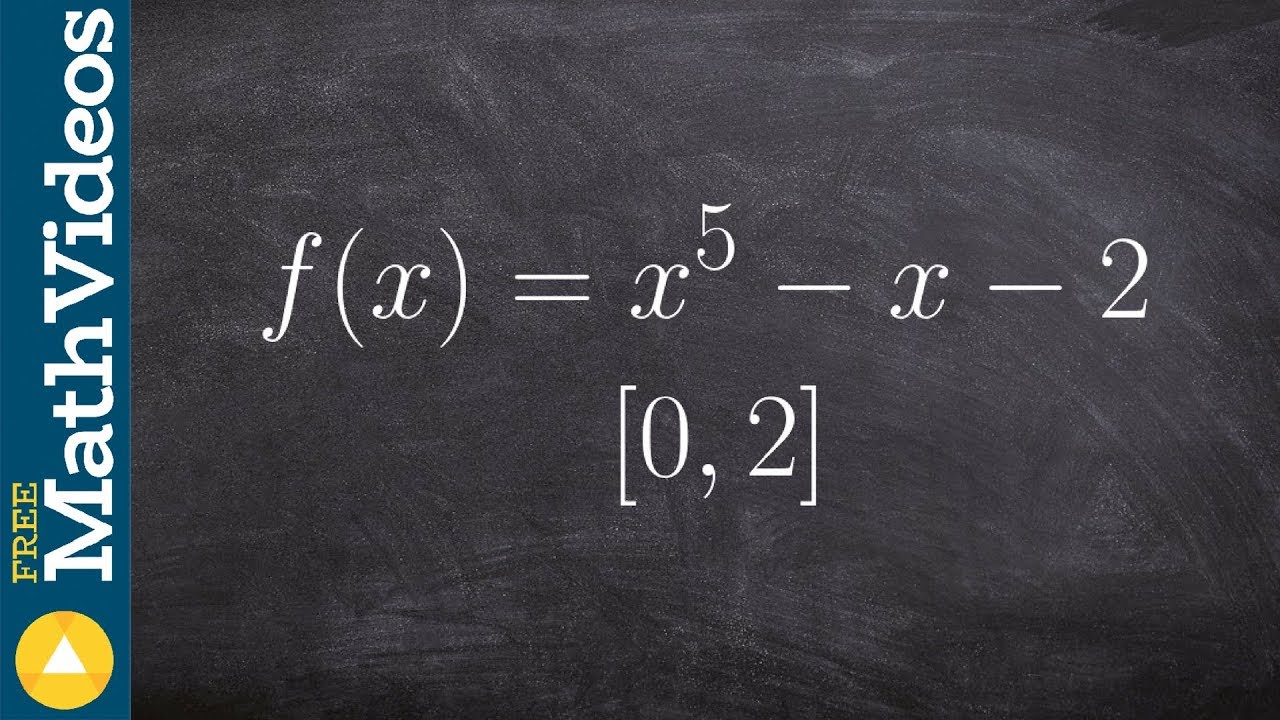
How to show that a solution exists to a functions using IVT

Justification with the intermediate value theorem: equation | AP Calculus AB | Khan Academy

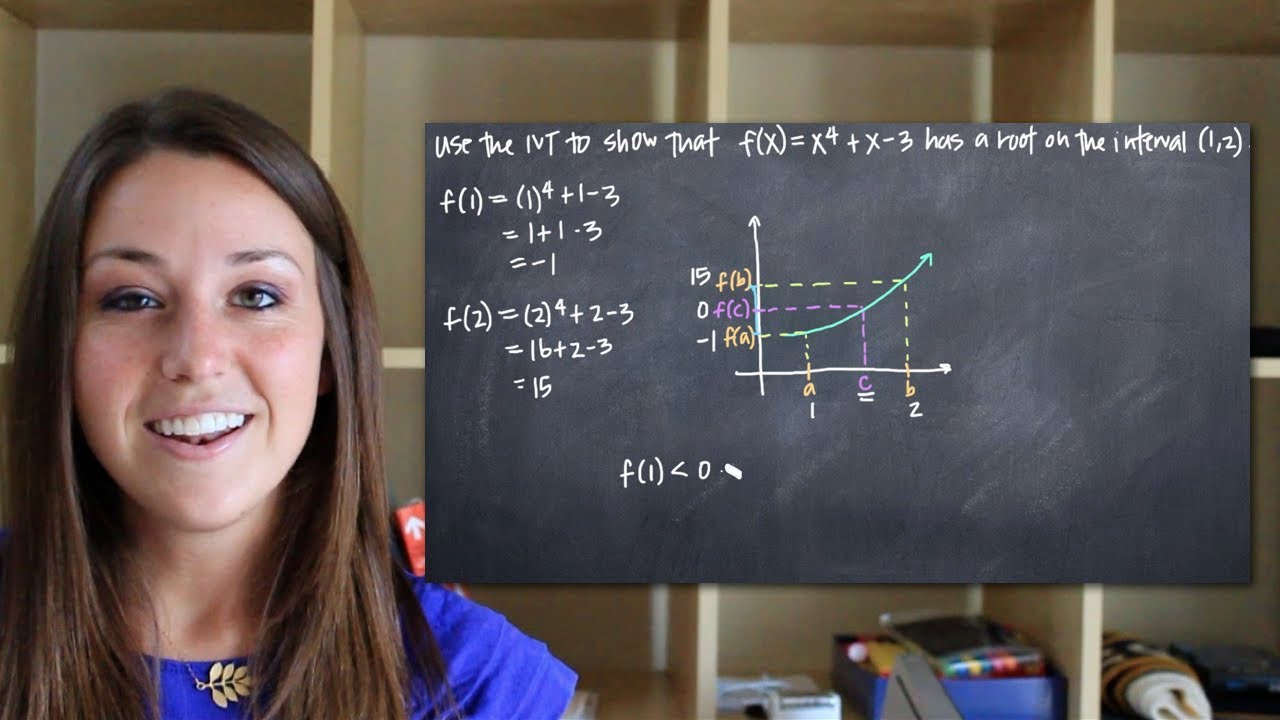
Intermediate value theorem to prove a root in an interval (KristaKingMath)

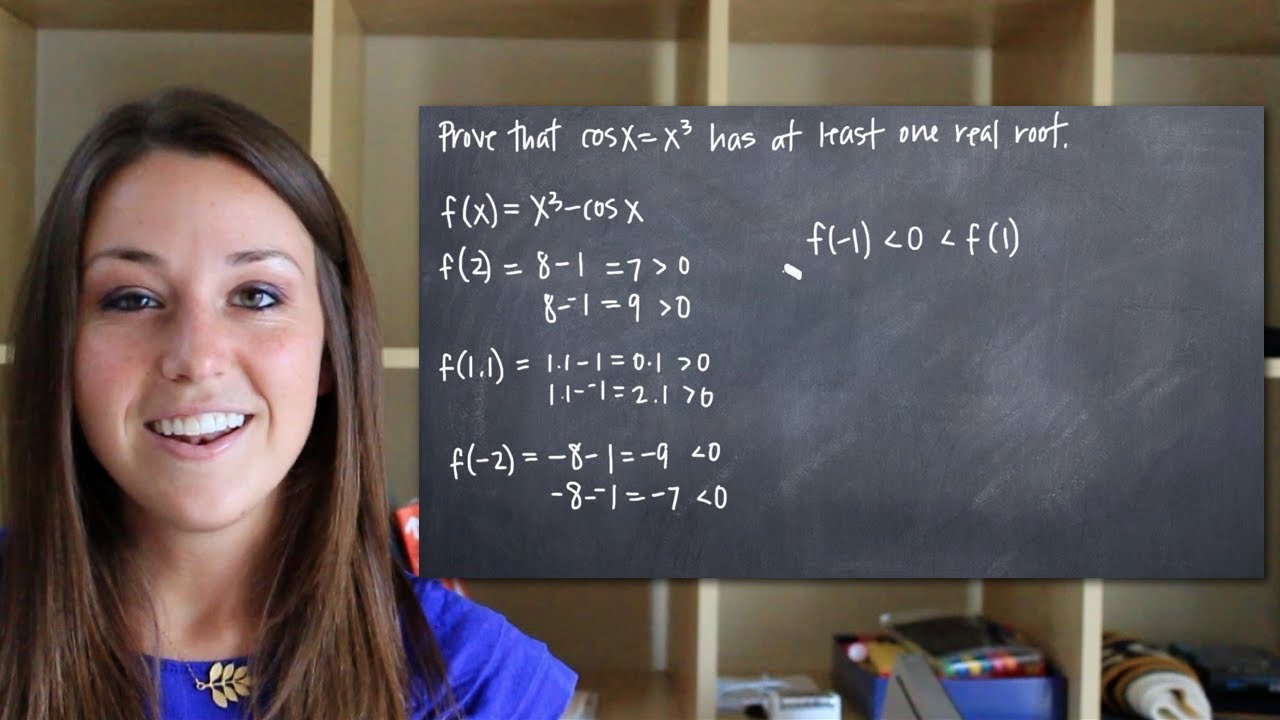
Prove the equation has at least one real root (KristaKingMath)

Intermediate value theorem example | Existence theorems | AP Calculus AB | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusRootsIVTPolynomialContinuous FunctionsTheorem ApplicationX-InterceptSolution FindingEducational ContentMath Tutorial