Intermediate Value Theorem, calculus 1 tutorial, showing a root of a function on an interval

blackpenredpen
1 Aug 201804:14
EducationalLearning
32 Likes 10 Comments

TLDRThis video tutorial demonstrates how to prove the existence of a root for the polynomial equation \( x^4 + x - 3 = 0 \) within the interval [1, 2]. The presenter explains that since the equation is already set to zero, it can be defined as a continuous function, f(x). By evaluating the function at the endpoints of the interval, showing that f(1) is negative and f(2) is positive, the video applies the Intermediate Value Theorem to conclude that there must be a root within the interval. The process is clear and emphasizes the importance of the function's continuity for the theorem to apply.

Takeaways
  • 📐 The goal is to show that a given equation has a root in the interval (1, 2).
  • ✏️ The equation is already set to equal 0, defining it as function f(x).
  • 📈 The function is defined as f(x) = x^4 + x - 3, which is a polynomial.
  • 🔍 Polynomials are continuous functions with no fractions, square roots, or denominators.
  • 🔲 The continuity of f(x) on the interval (1, 2) is established.
  • 🔢 Evaluating f(1) gives -1, indicating f(1) < 0.
  • 🔢 Evaluating f(2) gives 15, indicating f(2) > 0.
  • 📉 A sketch shows that f(1) is below the x-axis and f(2) is above the x-axis.
  • 📊 By the Intermediate Value Theorem, a continuous function that changes sign must cross the x-axis, indicating a root in (1, 2).
  • 🔍 The process can be refined by checking intermediate values like f(1.5) to narrow down the root's location.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is to demonstrate how to prove that a given equation has a root on the interval (1, 2).

  • What is the equation presented in the video?

    -The equation presented is \( x^4 + x - 3 \), which is already set to equal zero and is defined as the function \( f(x) \).

  • Why is the function considered continuous on the interval (1, 2)?

    -The function is considered continuous because it is a polynomial without any fractions, square roots, or other discontinuities.

  • What is the Intermediate Value Theorem and how does it apply here?

    -The Intermediate Value Theorem states that if a function is continuous on a closed interval and takes on different signs at the endpoints, then there must be at least one root within that interval. It applies here because the function changes sign between \( f(1) \) and \( f(2) \).

  • What is the result of plugging in x = 1 into the function?

    -Plugging in x = 1 into the function yields \( 1^4 + 1 - 3 = -1 \), which is less than 0.

  • What is the result of plugging in x = 2 into the function?

    -Plugging in x = 2 into the function yields \( 2^4 + 2 - 3 = 16 + 2 - 3 = 15 \), which is greater than 0.

  • What does the change in sign from \( f(1) \) to \( f(2) \) indicate?

    -The change in sign indicates that the function crosses the x-axis, implying the existence of at least one root between x = 1 and x = 2.

  • What is the significance of the function being a polynomial in this context?

    -The significance is that polynomials are continuous and differentiable everywhere, which allows for the application of the Intermediate Value Theorem without concerns about discontinuities.

  • How can one further narrow down the interval to find the root?

    -One can further narrow down the interval by evaluating the function at additional points within the interval, such as \( f(1.5) \), and observing the sign changes to approximate the location of the root more closely.

  • What is the conclusion of the video regarding the existence of a root?

    -The conclusion is that, by the Intermediate Value Theorem, there must be a root of the equation on the interval (1, 2) because the function is continuous and changes sign over that interval.

Outlines
00:00
📚 Demonstrating the Existence of a Root

The video script begins with the presenter's intention to demonstrate the existence of a root for a given equation on the interval (1, 2). The equation, already set to zero, is defined as a function f(x) = x^4 + x - 3. The presenter emphasizes that the function is a polynomial, hence continuous, with no fractions or square roots that could disrupt its continuity. The script then proceeds to evaluate the function at the endpoints of the interval, showing that f(1) is negative and f(2) is positive, which, according to the Intermediate Value Theorem, guarantees the existence of at least one root within the interval.

Mindmap
Keywords
💡Root
A 'root' in mathematics, particularly in the context of equations, refers to a value of the variable that makes the equation true, often resulting in a value of zero. In the video, the presenter is demonstrating how to show that the given equation has a root within the interval 1 to 2, which is a fundamental concept in solving equations and finding their solutions.
💡Equation
An 'equation' is a statement that asserts the equality of two expressions, typically involving one or more variables. In the script, the equation is already set to equal zero, which simplifies the process of finding a root, as the focus is on when the function equals zero.
💡Function
A 'function' in mathematics is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output. The script defines the equation as a function, f(x), which is then used to analyze the behavior of the equation within a specific interval.
💡Interval
In mathematics, an 'interval' refers to a set of real numbers with a lower and upper bound. The script mentions the interval 1, 2, which is the range within which the presenter is trying to find a root of the function.
💡Continuous Function
A 'continuous function' is a function that does not have any abrupt changes in value, meaning it does not have any breaks or jumps. The script emphasizes that the function is continuous on the interval 1, 2, which is crucial for applying the Intermediate Value Theorem.
💡Polynomial
A 'polynomial' is an expression consisting of variables and coefficients, involving only the operations of addition, subtraction, and multiplication, and non-negative integer exponents of variables. The function defined in the script is a polynomial, which is inherently continuous and differentiable everywhere.
💡Intermediate Value Theorem
The 'Intermediate Value Theorem' is a fundamental theorem in calculus that states if a function is continuous on a closed interval and takes on different signs at the endpoints, then it must take on every value between those endpoints. The script uses this theorem to conclude that there is a root within the interval 1, 2.
💡Endpoint
An 'endpoint' in the context of an interval refers to the starting or ending value of that interval. The script checks the values of the function at the endpoints 1 and 2 to determine the signs of the function at these points.
💡X-axis
The 'x-axis' in a graph represents the horizontal axis, and in the context of the script, it is used to visualize when the function crosses this axis, which corresponds to the function having a value of zero, indicating a root.
💡Sketch
A 'sketch' in the context of the script refers to a rough visual representation of the function's behavior, helping to visualize how the function values change as the variable x moves through the interval, and to identify where the function might cross the x-axis.
💡Differentiable
A function is 'differentiable' at a point if it has a derivative at that point, meaning the function's rate of change can be calculated. Although not explicitly mentioned in the script, the fact that the function is a polynomial implies it is differentiable everywhere, which is an important property for many mathematical analyses.
Highlights

The video demonstrates how to prove that a given equation has a root within the interval (1, 2).

The equation is already set to zero and is defined as the function f(x).

The function f(x) is a polynomial equation: x^4 + x - 3.

The absence of fractions, radicals, or other discontinuities indicates the function is continuous.

The function is continuous on the interval (1, 2), which is a key requirement for the Intermediate Value Theorem.

Checking the endpoints of the interval by plugging in x = 1 and x = 2.

Calculating f(1) results in a negative value, indicating the function crosses below the x-axis.

Calculating f(2) results in a positive value, indicating the function crosses above the x-axis.

The function must cross the x-axis between x = 1 and x = 2 due to its continuous nature.

The Intermediate Value Theorem is invoked to conclude the existence of a root in the interval.

The function's continuity is emphasized as the basis for the theorem's application.

An additional method is suggested to narrow down the root's location by checking f(1.5).

The video provides a clear and concise explanation of proving the existence of a root using the Intermediate Value Theorem.

The importance of the function being a polynomial and its implications for continuity are highlighted.

The process is simplified by focusing on the function's continuity and the theorem's application.

The video concludes with a summary of the steps taken to prove the existence of a root within the specified interval.

Transcripts

Browse More Related Video

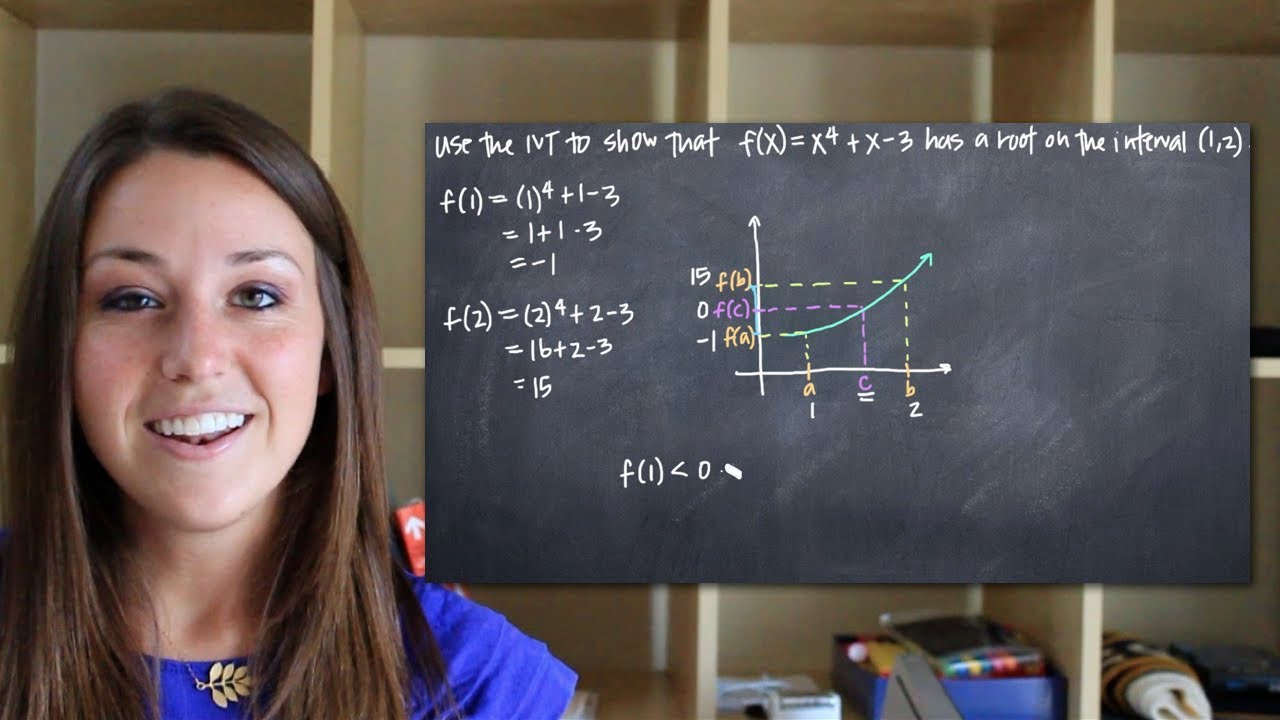
Intermediate value theorem to prove a root in an interval (KristaKingMath)

How to show that a solution exists to a functions using IVT

Intermediate Value Theorem Explained - To Find Zeros, Roots or C value - Calculus

Justification with the intermediate value theorem: equation | AP Calculus AB | Khan Academy

Intermediate Value Theorem: show function has at least one solution -- CALCULUS

Using the Intermediate Value Theorem Examples

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Math TutorialRoot FindingPolynomialsCalculusContinuous FunctionsIntermediate Value TheoremMathematicsEducationalSTEM LearningProblem Solving