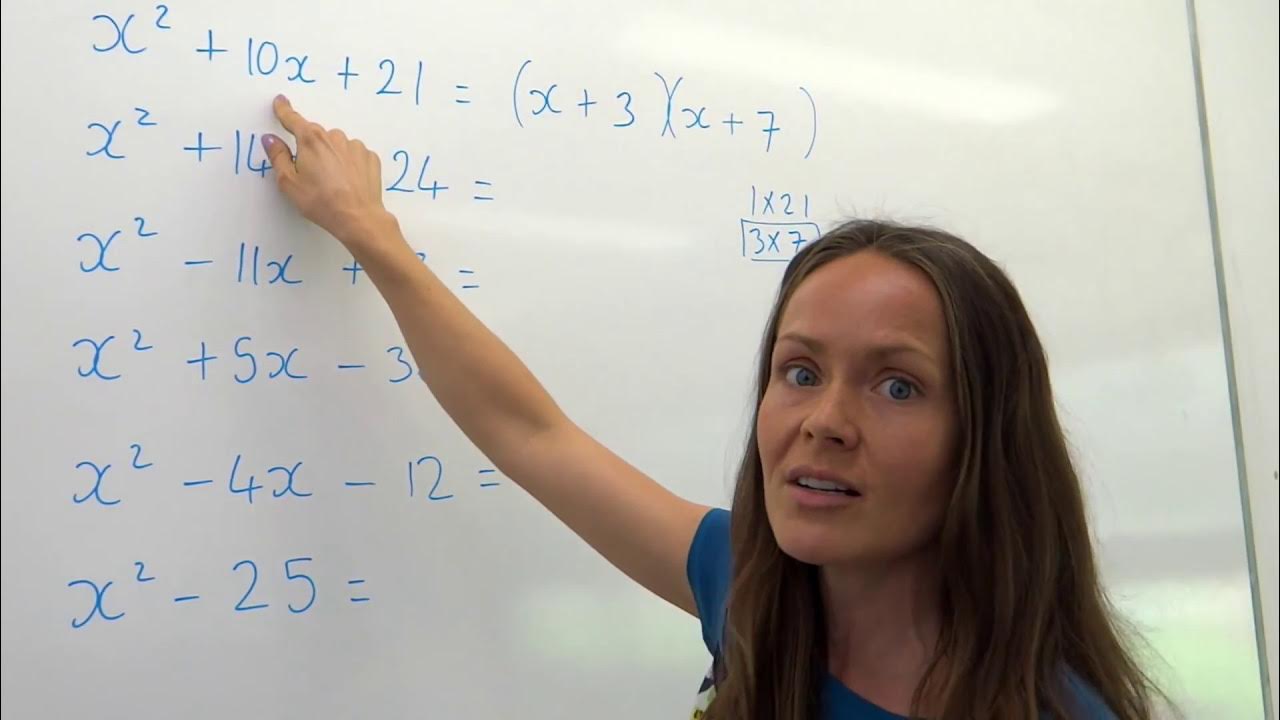Factoring Quadratic Expressions Pt. 1

MonkiMath
16 May 201505:52
EducationalLearning
32 Likes 10 Comments

TLDRThis introductory tutorial video focuses on factoring quadratic expressions with a leading coefficient of one. It explains the anatomy of quadratic expressions and demonstrates the factoring process through examples, including positive and negative constant terms. The video teaches how to identify the correct pairs of numbers that multiply to the constant term and add up to the linear coefficient, emphasizing the importance of considering both positive and negative factors when the middle term is negative. Stay tuned for the next part of the series.

Takeaways
  • 📚 The video is an introduction to a series of tutorials on factoring quadratic expressions.
  • 📐 The focus of the first tutorial is on quadratic expressions with a leading coefficient of one.
  • 🔍 A quadratic expression is typically in the form of ax^2 + bx + c, where 'a' is the leading coefficient and 'c' is the constant term.
  • ⚠️ There are special cases for when the leading coefficient 'a' is equal to one, which is the main topic of this tutorial.
  • 🔑 The leading coefficient is crucial as it determines the method of factoring the quadratic expression.
  • 📝 The first example provided is x^2 + 7x + 12, which demonstrates the process of factoring by finding pairs that multiply to the constant term and add up to the middle coefficient.
  • 🧩 The method involves identifying two numbers that multiply to the constant (12 in the example) and add up to the middle term (7x).
  • 📉 In the second example, the constant term is negative, and the tutorial explains how to consider both positive and negative factors to find the correct pair.
  • 🔄 The process involves adding the factors to check if they equal the middle coefficient, with attention to the sign.
  • 📈 The third example shows a scenario where the constant term is positive but the middle term is negative, emphasizing the importance of considering negative factors as well.
  • 💡 A tip provided is to always check negative factors when there is a negative sign in the second or third terms of the quadratic expression.
  • 👋 The tutorial concludes with an invitation to watch the next part of the series.
Q & A

  • What is the main topic of the introductory video?

    -The main topic of the introductory video is to teach how to factor quadratic expressions with a leading coefficient of one.

  • What is the general form of a quadratic expression?

    -The general form of a quadratic expression is ax^2 + bx + c, where a, b, and c are constants, with 'a' being the leading coefficient and 'c' being the constant term.

  • What are the two special cases mentioned in the script for the leading coefficient 'a'?

    -The two special cases mentioned are when the leading coefficient 'a' is equal to one, which is the focus of this tutorial, and when 'a' is different from one, which will be covered in another tutorial.

  • How does the constant term 'c' influence the factoring of a quadratic expression?

    -The constant term 'c' is determinant in the way we factor quadratic expressions, as it affects the possible pairs of factors that can be used to create the binomials for factoring.

  • What is the first example of a quadratic expression given in the script?

    -The first example given is x^2 + 7x + 12.

  • How are the factors of the constant term in the first example determined?

    -The factors of the constant term 12 are considered, and the pair that adds up to the middle term (7x) is chosen. In this case, the pair 3 and 4 is selected because 3 + 4 = 7.

  • What is the significance of the middle term in factoring quadratic expressions?

    -The middle term in a quadratic expression is significant because it is the product of the outer and inner terms of the binomials when the quadratic is factored.

  • What is the method used in the script to determine the correct pair of factors for the constant term?

    -The method involves listing the factors of the constant term and then adding each pair to see which gives the sum equal to the middle term of the quadratic expression.

  • What happens when the constant term has a negative number, as shown in the second example?

    -When the constant term has a negative number, both positive and negative factors must be considered to find the pair that, when added, gives the middle term of the quadratic expression.

  • What is the tip given in the script for dealing with negative signs in the quadratic expression?

    -The tip is to always check the negative factors of the constant term when there is a negative sign in either the second or third terms of the quadratic expression.

  • What is the third example in the script, and what is unique about it?

    -The third example is x^2 - 7x + 10. It is unique because the constant term is positive, but the middle term is negative, requiring consideration of negative factors for the constant term.

Outlines
00:00
📚 Introduction to Factoring Quadratic Expressions

This paragraph introduces a new series of tutorials focused on factoring quadratic expressions, specifically starting with those having a leading coefficient of one. The anatomy of a quadratic expression is explained, highlighting the leading term, the leading coefficient, and the constant term. The importance of these components is emphasized, especially in determining the method of factoring. The tutorial begins with an example, x^2 + 7x + 12, demonstrating the process of factoring by finding two numbers that multiply to the constant term and add up to the middle term. The significance of the middle term as the sum of the products of the two numbers chosen is also discussed.

05:00
🔍 Factoring Quadratics with Negative Constants

The second paragraph continues the tutorial by addressing quadratic expressions with negative constant terms. It illustrates the process of factoring with an example that includes negative 18 as the constant, showing how to consider both positive and negative factors to find the correct pair that sums up to the middle term. The paragraph explains the selection process using a factor table and emphasizes the importance of matching the signs found in the table to the signs in the factored expression. The example concludes with the correct factorization, demonstrating the method for handling negative constants in quadratic expressions.

Mindmap
Keywords
💡Quadratic Expression
A quadratic expression is a polynomial equation of degree two, typically in the form of \( ax^2 + bx + c \), where \( a \), \( b \), and \( c \) are constants, and \( x \) is a variable. In the context of the video, the focus is on factoring these expressions, which involves rewriting them as the product of two binomials. The script provides examples of how to identify and factor such expressions, emphasizing the importance of the leading coefficient and the constant term in the process.
💡Leading Coefficient
The leading coefficient in a quadratic expression is the coefficient of the \( x^2 \) term, which is denoted by 'a' in the standard form. It plays a crucial role in the factoring process, especially when the leading coefficient is one, as it simplifies the expression to a form that is easier to factor. The video script begins by discussing this special case where the leading coefficient is one, setting the stage for more complex scenarios in subsequent tutorials.
💡Factoring
Factoring, in the context of algebra, is the process of breaking down a polynomial into a product of its factors. The video script discusses factoring specifically for quadratic expressions, showing how to decompose them into two binomial expressions. The method involves finding two numbers that multiply to the constant term and add up to the coefficient of the linear term ('b').
💡Constant Term
The constant term in a quadratic expression is the term without the variable, represented by 'c' in the standard form \( ax^2 + bx + c \). It is a determinant in the factoring process, as the factors of this term will dictate the possible pairs that can be used in the binomials during factoring. The script illustrates how the constant term influences the selection of numbers to be placed in the parentheses during the factoring of quadratic expressions.
💡Binomial
A binomial is an algebraic expression composed of two terms, typically in the form of \( (x + y) \) or \( (x - y) \). In the video, binomials are the end result of factoring a quadratic expression. The script demonstrates how to rewrite a quadratic expression as the product of two binomials, which is a fundamental technique in algebra for simplifying and solving equations.
💡Anatomy of a Quadratic Expression
The anatomy of a quadratic expression refers to understanding the structure and components of such an expression. The video script introduces the concept by breaking down the standard form of a quadratic into its leading term, leading coefficient, linear term, and constant term. This understanding is essential for the factoring process, as it helps identify the parts of the expression that need to be manipulated.
💡Special Cases
The script mentions two special cases in the factoring of quadratic expressions: when the leading coefficient is one and when it is different from one. These special cases are important because they affect the approach to factoring. The video focuses on the first special case, providing a foundation for understanding how to handle more complex scenarios in the future.
💡Middle Term
The middle term of a quadratic expression is the 'bx' term, which is linear in nature. In the script, the middle term is crucial for determining the correct pair of numbers to use in the binomials during factoring. The video explains that the middle term is the sum of the products of the numbers chosen for the binomials, which must add up to the coefficient 'b'.
💡Factors of a Number
Factors of a number are the integers that can be multiplied together to produce that number. In the context of the video, the factors of the constant term are used to find the two numbers that will be placed in the binomials during factoring. The script demonstrates how to consider the factors of the constant term to determine the correct numbers for the binomial expressions.
💡Negative Constant Term
When the constant term in a quadratic expression is negative, it introduces a level of complexity in the factoring process. The video script provides an example where the constant term is negative and explains how to consider both positive and negative factors to find the correct pair of numbers for the binomials. This is an important consideration when the middle term is also negative.
💡Positive and Negative Factors
The video script highlights the importance of considering both positive and negative factors of the constant term, especially when dealing with a negative middle term in a quadratic expression. This consideration ensures that the correct pair of numbers is found to complete the factoring process, as demonstrated in the script's examples.
Highlights

Introduction to a sequence of tutorials on factoring quadratic expressions.

Focus of the first video: expressions with a leading coefficient of one.

Anatomy of a quadratic expression: ax^2 + bx + c.

Explanation of terms: leading term, leading coefficient, and constant term.

Importance of the leading coefficient in determining special cases.

First example: factoring x^2 + 7x + 12.

Steps to factor: identify two numbers that multiply to the constant term (c) and add to the middle term (b).

Using pairs of factors: (1, 12), (2, 6), (3, 4) and choosing the pair (3, 4) because they add to 7.

Factoring result: (x + 3)(x + 4).

Second example: factoring x^2 + 7x - 18.

Consideration of positive and negative pairs of factors for a negative constant term.

Using pairs of factors: (1, -18), (2, -9), (3, -6), (6, -3), (9, -2), (18, -1) and choosing (9, -2) because they add to 7.

Factoring result: (x + 9)(x - 2).

Third example: factoring x^2 - 7x + 10.

Consideration of negative pairs of factors when the middle term is negative.

Using pairs of factors: (1, 10), (2, 5) and negative pairs (-1, -10), (-2, -5) and choosing (-2, -5) because they add to -7.

Factoring result: (x - 2)(x - 5).

Tip: Always check negative factors when there is a negative sign in the quadratic expression.

Conclusion and introduction to the next video in the series.

Transcripts

Browse More Related Video

The Maths Prof: Factorising Quadratics (putting into double brackets)

Factoring Trinomials - Quick & Simple

Factoring Quadratics... How? (NancyPi)

Factoring Trinomials

GCSE Maths - Factorising Quadratics - Part 1 - (When the x^2 Coefficient is 1) - #50

Solving Quadratics by Factoring

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Quadratic FactoringMath TutorialLeading CoefficientAlgebra LessonsEducational ContentMathematics TipsFactoring TechniquesMath EducationVideo SeriesProblem Solving